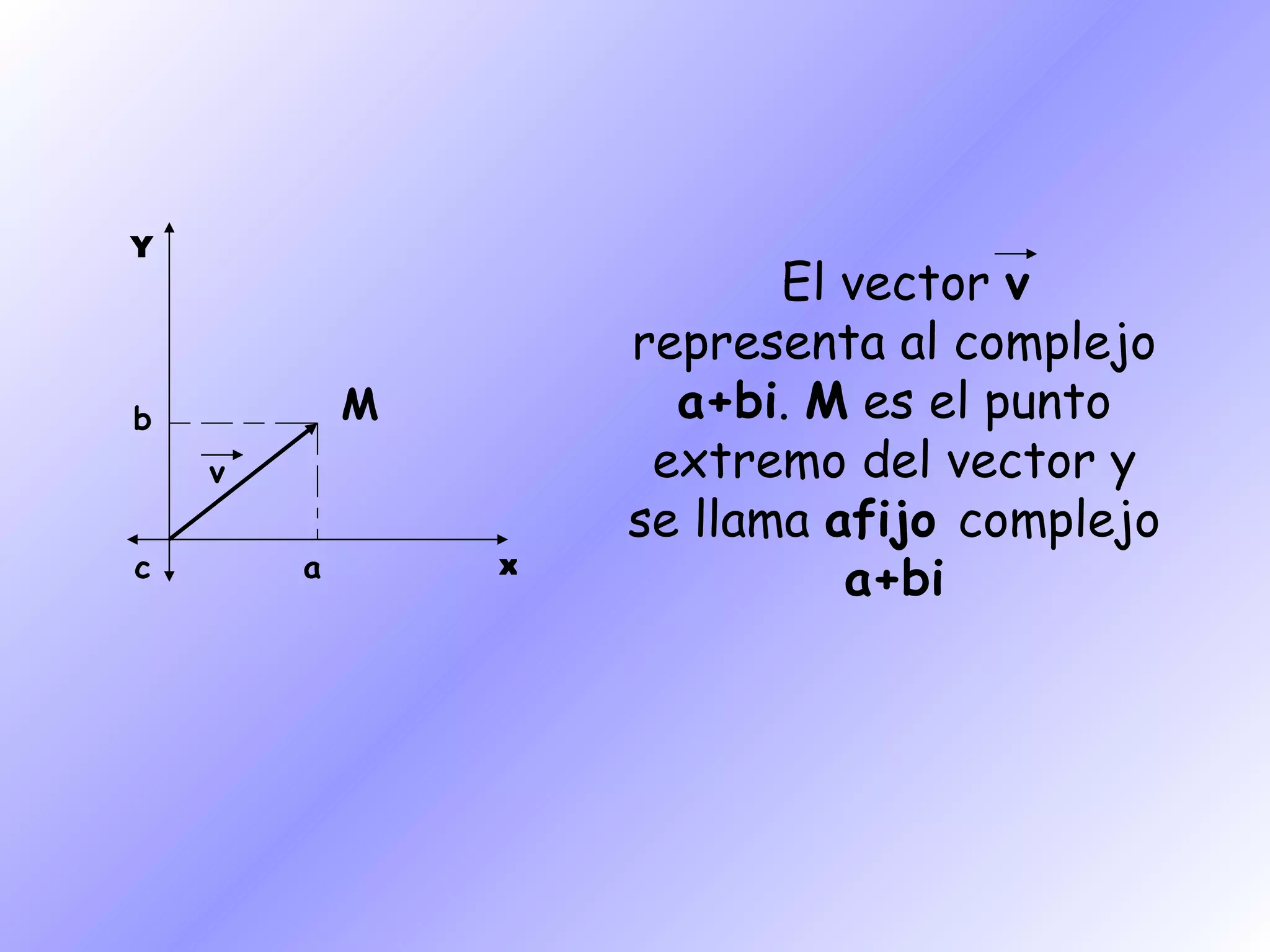
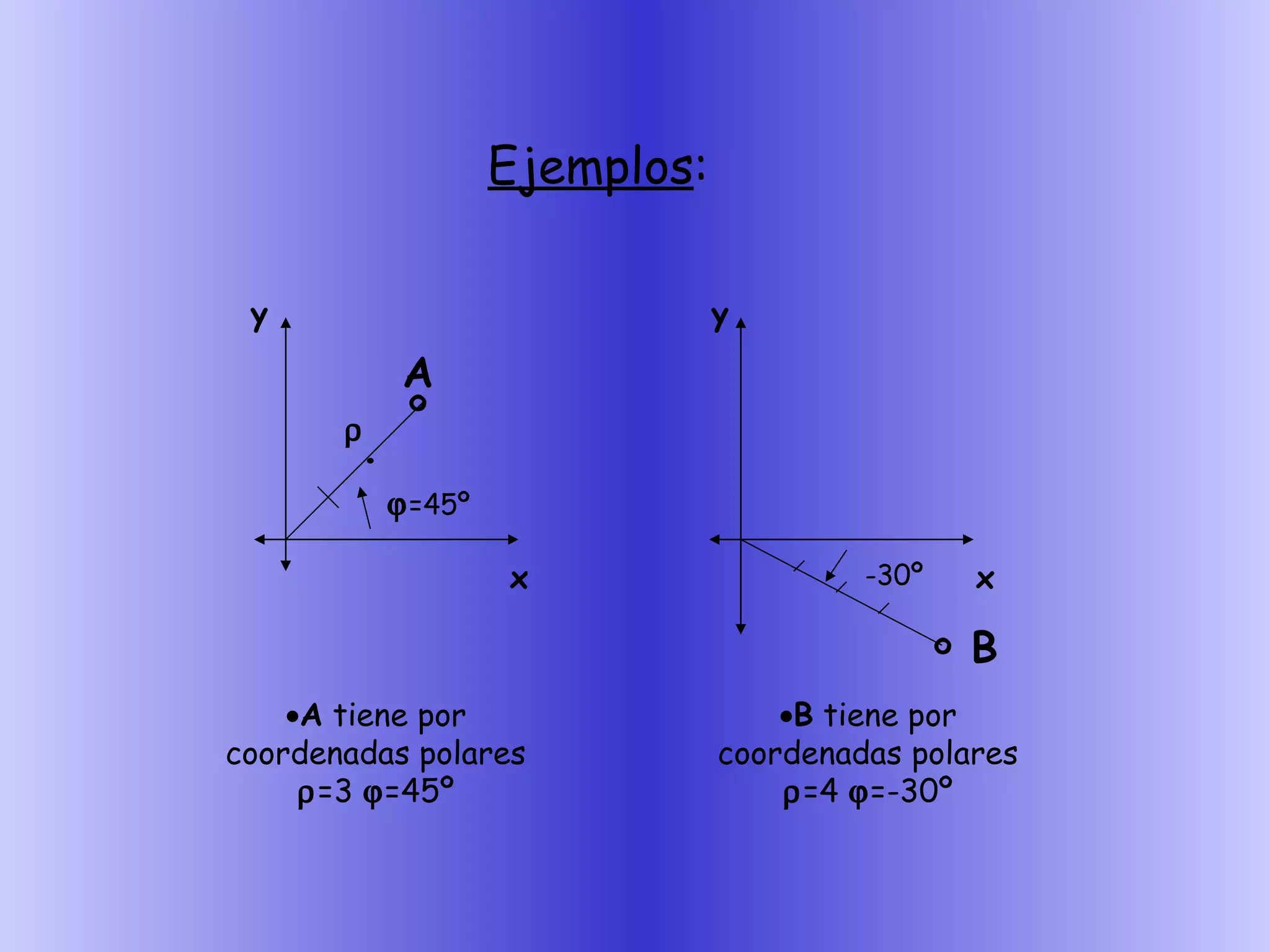
Este documento presenta los números complejos, incluyendo su representación como a + bi, donde a es la parte real y b la parte imaginaria. Explica cómo representarlos geométricamente en un plano cartesiano y también en coordenadas polares. Finalmente, cubre las operaciones con números complejos como suma, producto y potencias de i.

1. Alumnos : Gonzalo Nisi y Alejandro Lasconi Curso : 3º 2ª Escuela de enseñanza técnica particular incorporada “ Sagrada Familia ” Nº 8180 SPEP E. Zeballos 1850 Casilda Profesor : Héctor Andrés Crenna Fecha de Inicio : 23/06/08 Fecha de Entrega :01/09/08 Trayecto Técnico Profesional Módulo : Op., Mant. Y Ens. de Comp. de Equipos Electromecánicos T.P. :2

2. NÚMEROS COMPLEJOS

3. Índice 4- LOS NÚMEROS COMPLEJOS 8- LOS NÚMEROS COMPLEJOS Y SUS OPERACIONES 11- REPRESENTACIÓN GEOMÉTRICA DE LOS COMPLEJOS 15- FORMA POLAR DE LOS NÚMEROS COMPLEJOS 18- POTENCIAS DE i

4. LOS NÚMEROS COMPLEJOS Hemos resuelto ecuaciones como –3x=2 para la que no encontramos solución en N , ni en Z , pero sí en Q , la solución es x=-2/3 . Para la ecuación x 2 =2 solo encontramos solución en R , pues x= .

5. Siguiendo esta secuencia, se puede plantear la siguiente ecuación: X 2 + 1=0 Podrás comprobar que no tiene solución ni en N , ni en Z , ni en Q , ni en R .

6. * Una solución consiste en asignarle a x el valor , pero sabemos que esto no es posible, porque la radicación no permite tomar radicandos negativos si el índice es par.

7. Por eso, se introdujo el símbolo i (que quiere decir imaginarius ) para nombrar a . Por lo tanto si i = i 2 =-1

8. LOS NÚMEROS COMPLEJOS Y SUS OPERACIONES Los números complejos son de la forma a+bi , donde a y b son números reales cualesquiera e i es un símbolo para la unidad imaginaria.

9. · Reglas para trabajar con los complejos : Si Z 1 = a + bi Z 2 = c + di 1.IGUALDAD: Z 1 =Z 2  a=c y b=d 2.SUMA: Z 1 + Z 2 = (a+bi) + (c+di) 3.PRODUCTO: Z 1 . Z 2 = (a+bi).(c+di)

10. Ejemplo : Z =5+3i Z es un número complejo . Re( z )=5 * La parte real de Z es 5. Im( z )=3 * La parte imaginaria de Z es 3. * Si a = 0 y b 0 resulta imaginario puro . * Si a 0 y b = 0 resulta número real .

11. REPRESENTACIÓN GEOMÉTRICA DE LOS COMPLEJOS · A cada número complejo expresado en la forma binómica : a+bi · Se le puede asignar un PAR ORDENADO: (a;b)

12. A cada par ordenado le asignamos un punto del plano: x Y (a;b) a b . Eje x = Eje Real Eje y = Eje Imaginario

13. El número complejo a+bi se representa con un vector que tiene su origen en el origen de coordenadas y su extremo en el punto (a,b).

14. x Y M c a b v El vector v representa al complejo a+bi . M es el punto extremo del vector y se llama afijo complejo a+bi

15. FORMA POLAR DE LOS NÚMEROS COMPLEJOS El complejo 3+2i está asociado al punto P=(3,2) mas también c/punto del plano queda determinado por su distancia al origen de coordenadas |OP|=  y por el ángulo de OP con el eje positivo de x.

17. Ejemplos :  =45º .  º A y x x y -30º º B  A tiene por coordenadas polares  =3  =45º  B tiene por coordenadas polares  =4  =-30º

18. POTENCIAS DE i Teniendo en cuenta que i 2 =-1 calculamos las sucesivas potencias de i , conveniendo en definir: i 0 =1 i 1 =i i 2 =-1 i 3 =-i

19. A partir de la cuarta potencia los números 1 , i , -1 , -i se repiten periódicamente, así: i 4 =i 3 .i=-i.i=-i 2 =1

20. Para calcular una potencia cualquiera de i , por ejemplo i n , debemos hallar el resto de la división de n.4 . De esta manera si entonces n=4.q+r Luego: i n =i 4.q+r =i 4q .i r =(i 4 ) q .i r =1 q .i r =i r I n =i r donde r es el resto de la división de n por 4 4 n q r