Trabajo

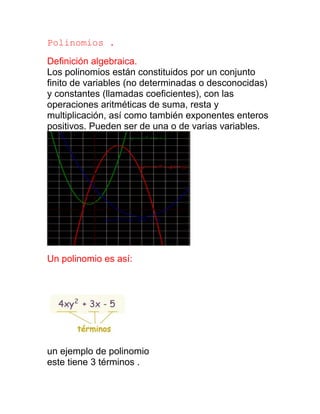
1. Polinomios .
Definición algebraica.
Los polinomios están constituidos por un conjunto
finito de variables (no determinadas o desconocidas)
y constantes (llamadas coeficientes), con las
operaciones aritméticas de suma, resta y
multiplicación, así como también exponentes enteros
positivos. Pueden ser de una o de varias variables.
Un polinomio es así:
un ejemplo de polinomio
este tiene 3 términos .

2. Que se pueden combinar usando:
+ - × sumas, restas y multiplicaciones...
círculo ... ¡pero no divisiones! círculo
Estas reglas hacen que los polinomios sean simples,
¡así es fácil trabajar con ellos!
Estos son polinomios:
3x
x - 2
3xyz + 3xy2z - 0.1xz - 200y + 0.5
Y estos no son polinomios
2/(x+2) no lo es, porque dividir no está permitido
3xy-2 no lo es, porque un exponente es "-2" (los
exponentes sólo pueden ser 0,1,2,...)
Pero esto sí está permitido:
x/2 está permitido, porque también es (½)x (la
constante es ½, o 0.5)
también 3x/8 por la misma razón (la constante es 3/8,
o 0.375)
Grado
El grado de un polinomio con una sola variable es el
mayor exponente de esa variable.
Se define el grado de un monomio como el
exponente de su variable.

3. El grado de un polinomio es el del monomio de mayor
grado.
Ejemplo:
4x3-x-3 El grado es 3 (el mayor exponente de x)
¿Son polinomios o no?
polinomio
Ejemplos
P(x) = 2, polinomio de grado cero (el polinomio solo
consta del término independiente).
P(x) = 3x + 2, polinomio de grado uno.
P(x) = 3x² + 2x, polinomio de grado dos.
P(x) = 2x3+ 3x + 2, polinomio de grado tres.
P(x) = 4x4+ 4x + 2, polinomio de grado cuatro.
P(x) = 2x5+ 3x + 1, polinomio de grado cinco.
Operaciones con polinomios .
Los polinomios se pueden sumar y restar agrupando
los términos y simplificando los monomios
semejantes. Para multiplicar polinomios se multiplica
cada término de un polinomio por cada uno de los
términos del otro polinomio y luego se simplifican los

4. monomios semejantes.
Ejemplos de funciones polinómicas.
Note que las gráficas representan a las funciones
polinómicas y no a los polinomios en sí, pues un
polinomio solo es la suma de varios monomios
Polinomio de grado 2:
f(x) = x2 - x - 2= (x+1)(x-2).
Polinomio de grado 3:
f(x) = x3/5 + 4x2/5 - 7x/5 - 2=
1/5 (x+5)(x+1)(x-2).
Polinomio de grado 4:
f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5.

5. Polinomio de grado 5:
f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2.
Suma de polinomios.
Para sumar polinomios, sumamos entre sí aquellos
monomios que tengan la misma parte literal.
Por ejemplo, consideremos los polinomios
P(x)= 3x5 + 2x3 - 5x2 + 6 y Q(x) = 8x3 + 3x2 - x - 4
El polinomio resultante de la suma P(x) + Q(x)= 3x5 +
10x3 - 2x2 - x + 2
Fíjate, aquellos monomios cuya parte literal aparece
en un polinomio los hemos copiado y hemos sumado
aquellos monomios que tenían la misma parte literal:
2x3 + 8x3 = 10x3
-5x2 + 3x2 = -2x3
6 - 4 = 2

6. Resta de polinomios.
Para restar polinomios, restamos entre sí aquellos
monomios que tengan la misma parte literal.
Por ejemplo, consideremos los polinomios
P(x)= 3x5 + 2x3 - 5x2 + 6 y Q(x) = 8x3 + 3x2 - x - 4
El polinomio resultante de la resta P(x) - Q(x)= 3x5 - 6
x3 - 8x2 + x + 10
Fíjate, aquellos monomios cuya parte literal aparece
sólo en P(x) se dejan tal cual, a los que aparecen
sólo en Q(x) se les cambia el signo y restamos
aquellos monomios que tenían la misma parte literal:
2x3 - 8x3 = -6x3
-5x2 - 3x2 = -8x3
6 - (-4) = 10 .
Producto de polinomios.
Para multiplicar dos polinomios multiplicamos cada
monomio del primer polinomio por cada polinomio del
segundo. Luego sumamos aquellos monomios con la
misma parte literal.
Raíz de un polinomio
Diremos que un número x=a es raíz de un polinomio
P(x) si al evaluar P en a se anula, es decir, P(a)=0 .
Un polinomio es divisible por otro si al realizar la
división el resto es 0.
Por tanto, si a es raíz de un polinomio P(x), teniendo
en cuenta el teorema del resto, podemos afirmar que
P(x) es divisible por x-a.

7. Si a es una raíz de un polinomio entonces a divide al
término independiente.
Dado P(x) = cnxn + cn-1xn-1 +...+ c1x + c0 y sea a
una raíz de P
P(a) = cnan + cn-1an-1 +...+ c1a + c0 , al sea a una
raíz, P(a) = 0
cnan + cn-1an-1 +...+ c1a + c0 = 0 pasamos el
término independiente al segundo miembro y
sacamos factor común a a, queda a·( cnan-1 + cn-
1an-2 +...+ c1 ) = - c0 de aquí se deduce que la raíz
es divisor del término independiente.
Esto nos permite buscar las raíces entre los divisores
del término independiente
Factorizar un polinomio
Factorizar consiste en descomponer un polinomio
como producto de otros más simples. Cuando un
polinomio no se puede poner como producto de otros
más simples se dice que es irreducible.
Para factorizar un polinomio hallamos su raíces, si a
es una raíz de P(x), entonces P(x)=(x-a)·P1(x), así
hemos descompuesto P como producto de dos
polinomios, reiteramos el proceso, ahora con P1y
seguimos hasta que nos encontremos con un
polinomio irreducible.
Factoriza el polinomio P(x)=2x5 -3x3 +4x2 -9x + 6
Usamos la regla de Ruffini, los candidatos a raíz
serán los divisores de 6, es decir, 1, -1, 2, -1, 3, -2, 6,
-6.
Vamos probando hasta que encontremos un valor
cuyo resto es 0, repetimos el proceso con los

8. coeficientes del polinomio cociente hasta que no
podamos continuar, porque lleguemos a un polinomio
irreducible.
En el ejemplo hemos llegado a un momento en el que
no hemos encontrado raíces enteras 2x2 +3, con este
polinomio podemos continuar planteando una
ecuación de segundo grado, aún así no tiene raíces
reales por tanto es irreducible. En la figura de la
derecha se observa el proceso.
La factorización queda:
2x5 -3x3 +4x2 -9x + 6 =(x-1)2(x+2)(2x2 +3).
Logaritmo.
El logaritmo de un número, en una base dada, es el
exponente al cual se debe elevar la base para
obtener el número.
Se lee “logaritmo de x en base a es igual a y ”, pero
debe cumplir con la condición general de que a (la
base) sea mayor que cero y a la vez distinta de uno :
Para aclarar el concepto, podríamos decir que
logaritmo es solo otra forma de expresar la
potenciación, como en este ejemplo:

9. Que leeremos: logaritmo de 9 en base 3 es igual a 2
Esto significa que una potencia se puede expresar
como logaritmo y un logaritmo se puede expresar
como potencia.
El gráfico siguiente nos muestra el nombre que recibe
cada uno de los elementos de una potencia al
expresarla como logaritmo:
Entonces, podemos preguntar: ¿Que es el logaritmo?
El logaritmo es " el exponente " por el cual se ha
elevado una base para obtener la potencia .
Ejemplos:
1) logaritmos001
El resultado (2) es el exponente por el cual debemos
elevar la base (2) para obtener la potencia (4): 2 2 = 4
2) logaritmos002

10. El resultado (0) es el exponente por el cual debemos
elevar la base (2) para obtener la potencia (1): 2 0 = 1
3) logaritmos003
El resultado (y) es el exponente por el cual debemos
elevar la base (1/2) para obtener la potencia (0,25):
logaritmos004 , pero en este caso debemos despejar
el exponente y.
5)
Cuidado con esto, hay que recordarlo: Cuando la
base no aparece expresada se supone que ésta es
10:
, el 10 que indica la base, no se coloca,
se supone, así:
6)
Aquí, otra nota importante, para no olvidar: Los
logaritmos que tienen base e se llaman logaritmos
neperianos o naturales. Para representarlos se
escribe ln o bien L . La base e está implícita, no se
escribe:

11. Propiedades de los logaritmos
No existe el logaritmo de un número con base
negativa.
No existe el logaritmo de un número negativo
No existe el logaritmo de cero.
El logaritmo de 1 es cero.
El logaritmo de a en base a es uno.
El logaritmo en base a de una potencia en base a es
igual al exponente.
El logaritmo de un producto es igual a la suma de los
logaritmos de los factores:
El logaritmo de una potencia es igual al producto del
exponente por el logaritmo de la base:

12. .
Logaritmo de una potencia con igual base:
El logaritmo de una potencia de un número es igual al
producto entre el exponente de la potencia y el
logaritmo del número
Ej:
log6 6 3 = 3
logb bn = n, con b ≠ 1
Logaritmos de la base
El logaritmo de la base es igual a 1.

13. logb (b) = 1 ; con b ≠ 1.
Ej:
log5 (5) = 1 ⇔ 51 = 5
log6 (6) = 1 ⇔ 61 = 6
log12 (12) = 1 ⇔ 121 = 12
TRIGONOMETRÍA
Función potencia: traslaciones horizontales y
verticales

14. Las traslaciones verticales y horizontales son los
desplazamientos de una función en el sistema de
coordenadas (x, y). Si trasladamos la representación
gráfica de una función dada, obtendremos
representaciones de funciones relacionadas. Siempre
la grafica de la función trasladada será igual a la
original.
Si realizamos una traslación vertical de una función,
la gráfica se moverá de un punto a otro punto
determinado en el sentido del eje “y”, es decir, hacia
arriba o hacia abajo.
Ejemplo:

15. Si realizamos una traslación horizontal de una
función, la gráfica se moverá de un punto a otro punto
determinado en el sentido del eje “x”, es decir, hacia
la derecha o hacia la izquierda.
Ejemplo:

16. Las traslaciones tanto horizontales como verticales,
están ligadas al concepto de incremento o
decremento de un valor constante (que
denominaremos c), por lo cual son únicamente en
forma de suma o diferencia, y se expresan
matemáticamente de la siguiente forma .

17. Ejemplo:
Traslada la función f (x) = x2, 2 unidades a la derecha
y 3 unidades hacia arriba. Grafica.
- Si ocupamos la tabla anterior, quedaría en forma
matemática de la siguiente manera;
Grafica;

18. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO
AGUDO
Llamamos razones trigonométricas a las distintas
razones existentes entre los lados de un triángulo
rectángulo. Se define:
Seno de un ángulo como la razón entre el cateto
opuesto al ángulo y la hipotenusa.
Coseno de un ángulo como la razón entre el cateto
contiguo al ángulo y la hipotenusa.
Tangente de un ángulo como la razón entre el cateto
opuesto y el contiguo.

19. Cosecante de un ángulo como la razón entre la
hipotenusa y el cateto opuesto, de ahí se deduce que
la consecante es 1 entre el seno
Secante de un ángulo como la razón entre la
hipotenusa y el cateto contiguo, es 1 entre el coseno.
Cotangente de un ángulo es la razón entre el cateto
contiguo y el cateto opuesto, es 1 entre la tangente.

21. Ejemplos de aplicación de estas fórmulas

23. Dado el triangulo ABC, rectángulo en A, Si AB = 15
cm. y BD = 9 cm. ¿Cuánto mide AC y AD?
Aplicando el teorema referido a los catetos tenemos
que;
Entonces, CD = BC – BD = 25 - 9 = 16.

24. - Para calcular AC aplicamos nuevamente el teorema
referido a los catetos;
- Para calcular AD aplicamos el teorema referido a la
altura;
Respuesta: AC mide 20 cm. y AD mide 12 cm.
funciones inversas.
Encontrar funciones inversas. Aprende a
encontrar la fórmula de la inversa de una

25. función dada. Por ejemplo, encuentra la
inversa de f(x)=3x+2. ... Por ejemplo, si f ff
convierte a aa en b bb, entonces la inversa
debe convertir b bb en a aa.
Las razones trigonométricas no son funciones
biyectivas (1-a-1), por lo que no son invertibles. Para
que lo sean, es necesario restringir su dominio y así
poder hallar la función inversa.
Arcoseno
El arcoseno es la función inversa del seno. Es decir:
Al ser el arcoseno y el seno funciones inversas, su
composición es la identidad, es decir:
Su abreviatura es arcsen o sen-1.

26. -Dominio (x)
- Codominio (α)
Para poder definir la función inversa de una función,
necesariamente debe ser biyectiva. La función seno
no es inyectiva en el conjunto de los reales. Por
convención, se restringe el codominio al intervalo [-
π/2,π/2] para que la función seno sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcoseno:

27. Función exponencial.
La función exponencial, es conocida formalmente
como la función real ex, donde e es el número de
Euler, aproximadamente 2.71828.; esta función tiene
por dominio de definición el conjunto de los números
reales, y tiene la particularidad de que su derivada es
la misma función. Se denota equivalentemente como
f(x)=ex o exp(x), donde e es la base de los logaritmos
naturales y corresponde a la función inversa del
logaritmo natural.
En términos mucho más generales, una función real
E(x) se dice que es del tipo exponencial en base a si
tiene la forma
E (x) = K.a a la x
Crecimiento exponencial.
La expresión crecimiento exponencial se aplica a una
magnitud tal que su variación en el tiempo es
proporcional a su valor, lo que implica que crece muy
rápidamente en el tiempo:

28. Funciones exponenciales
Una función exponencial es aquella que está
modelada por
f(x) = ah(x) donde a > 0 y diferente de la unidad h(x)
una función en x.
Veamos algunos ejemplos de funciones
exponenciales
* y = Ae-kt * y = 2x
* y = (1/2)x * f(t) = 2e2t
Gráfica de una función exponencial
A la hora de hacer una grafica de una función

29. exponencial se deben tomar en cuenta dos casos, el
primero donde a > 1, y un segundo caso donde 0 < a
< 1.
Esto significa que la función exponecial se transforma
en una función constante si a = 1, es decir y = 1x = 1.
Análisis de la gráfica para el caso a > 1
Ejemplo tomemos f(x) = y = 2x
La función f(x) está definida para cualquier valor real
de la variable x.Primero tomamos una pequeña
muestra de valores para x y de esta manera obtener
f(x) en función de x para esto construiremos una
pequeña tabla que muestre estos valores.

30. Análisis de la gráfica del caso 0 < a < 1
Usemos de ejemplo f(x) = y = (1/2)x
La función f(x) está definida para cualquier valor real
de la variable x.Primero tomamos una pequeña
muestra de valores para x y de esta manera obtener
f(x) en función de x para esto construiremos una
pequeña tabla que muestre estos valores.

31. Propiedades de una función exponencial
1) El dominio de imágenes o función exponencial es
siempre positiva, y siempre esta funcion se encuentra
encima del eje x
2) El codominio de la función exponencial está
compuesto por todos los números reales positivos y
el dominio por todos los números reales
3) La grafica que representa una función exponencial
nunca hace intersepción con el eje x .Sólo existe una
intersepción con el eje y, en el punto (0 , 1).
4) Si a > 1 la función exponencial es creciente. Si 0 <
a < 1 la función exponencial es decreciente
5) Para a > 1, el eje x se convierte en una asíntota
horizontal de la gráfica por la izquierda, si 0 < a < 1 el
eje x es asíntota horizontal por la derecha
6) Para a > 1 cunado x tiende a infinito por la

32. izquierda, y = f(x) tiende a cero.Cuando x tiende a
infinito por la derecha, y = f(x) tiende a infinito.
Para 0 < a < 1 cunado x tiende a infinito por la
derecha, y = f(x) tiende a cero.Cuando x tiende a
infinito por la izquierda, y = f(x) tiende a infinito.
Todas estas propiedades se pueden observar
claramente en una gráfica que muestre los dos casos
juntos.
Muchas Gracias Por Su Atencion .
Espero Que Le Alla Gustado .
Alumno : Stiver Salazar .