Flexión: Tensiones máximas

Tema 5: Flexión: Tensiones
1
Prof.: Jaime Santo Domingo Santillana
E.P.S.-Zamora – (U.SAL.) - 2008
Tema 5 : FLEXIÓN: TENSIONES
G x
z
y
n
n
σMAX(COMPRESIÓN)
σMAX(TRACCIÓN)

2
5.1.- INTRODUCCIÓN
Una barra está solicitada a FLEXIÓN PURA cuando en sus secciones rectas
transversales actúan únicamente los momentos flectores: Mz y/o My. (Fig. 5.1.a)
En el caso de que a la vez que los momentos flectores Mz y/o My actúen también las
fuerzas cortantes Vy y/o Vz, se dice que está solicitada a FLEXIÓN SIMPLE.(Fig.
5.1.b)
Si sólo actuase uno de los dos momentos flectores: Mz o My se denomina: FLEXIÓN
SIMÉTRICA (Fig. 5.1.c)
Si el vector momento tiene las dos componentes: Mz y My se denomina: FLEXIÓN
ASIMÉTRICA (Fig. 5.1.d)
FLEXIÓN PURA
My
Mz
x
y
z
G
Fig.5.1.a
FLEXIÓN SIMPLE
G
Mz
My
Vz
z
x
y
Vy
Fig.5.1.b
Mz
x
y
z
G
FLEXIÓN SIMÉTRICA
Fig.5.1.c
FLEXIÓN ASIMÉTRICA
My
Mz
x
y
z
G
Fig.5.1.d

Sección 5.2: Fuerzas Cortantes y Momentos Flectores. Diagramas y relaciones entre ambos
3
5.2.-FUERZAS CORTANTES Y MOMENTOS FLECTORES. DIAGRAMAS Y
RELACIONES ENTRE AMBOS
Ejes de referencia
Sección con normal exterior positiva: n > 0
Sección con normal exterior negativa: n < 0
Convenio de signos para las fuerzas cortantes Vy , Vz
En una sección con normal exterior positiva (n > 0), las fuerzas cortantes Vy y Vz son
positivas, cuando llevan el mismo sentido de los semiejes positivos OY, OZ
respectivamente. Serán negativas en caso contrario.
En el caso de una sección con normal exterior negativa (n < 0) será al revés
Vy > 0 Vz > 0
O
y
z
x xn > 0n < 0
Fig.5.2
xn > 0n < 0
y
z
O
Vy
Vy
Vz
Vz
Fig.5.3

4
Convenio de signos para los momentos flectores Mz , My
Caso del momento flector Mz:
En una sección con normal exterior positiva (n > 0), el momento flector Mz será
positivo, cuando lleve el sentido contrario al del semieje OZ positivo . Será negativo en
caso contrario.
Mz > 0
x
y
-
Mz < 0 : la viga flexa (se dobla) hacia la parte negativa del eje y
x
y
Mz > 0 : la viga flexa (se dobla) hacia la parte positiva del eje y
+
Fig.5.5.a
xn > 0n < 0
y
z
O
Mz
Mz Fig.5.4
Fig.5.5.b

Sección 5.2: Fuerzas Cortantes y Momentos Flectores. Diagramas y relaciones entre ellos
5
Caso del momento flector My:
En una sección con normal exterior positiva (n > 0), el momento flector My será
positivo, cuando lleve el mismo sentido al del semieje OY positivo . Será negativo en
caso contrario.
x
z
y
+
My > 0 : la viga flexa (se dobla) hacia la parte positiva del eje z
Fig.5.7.a
x
z
y
-
My < 0 : la viga flexa (se dobla) hacia la parte negativa del eje z
xn > 0n < 0
y
z
O
My
My
Fig.5.6
Fig.5.7.b

6
Observación: El Mz es el único, que en las secciones n>o, se toma positivo si su sentido
es el contrario al semieje positivo correspondiente.
Diagramas de Fuerzas Cortantes y de Momentos Flectores
Éstos diagramas representarán las Fuerzas Cortantes y los Momentos Flectores en cada
una de las secciones de una viga, (al igual que en la sección 4.2 se estudiaron los
Diagramas de Fuerzas Normales) y gracias a ellos se podrán conocer los esfuerzos
máximos y las secciones donde éstos se darán.
Se desarrollarán los Diagramas de Fuerzas Cortantes y de Momentos Flectores a través
del siguiente ejemplo:
En una sección x cualquiera la Resultante y el Momento resultante de las fuerzas
exteriores serán:
Con lo cual, la Resultante y el Momento resultante de las fuerzas interiores serán:
O
y
z
x
F
P
x
L
Fig.5.8
O
y
z
x
F
P
x
n>0
F
F.x
P.x
P
Rext, Mext Fig.5.9.a
O
y
z
x
F
P
x
n>0
F
F.x
P.x
P
Rint, Mint Fig.5.9.b

Sección 5.2: Fuerzas Cortantes y Momentos Flectores: Diagramas y relaciones entre ellos
7
O
y
z
x
F
P
x
L
Fig.5.10
O
y
z
x
F
P
x
n>0
F
F.x
P.x
P
Rint, Mint
x
x
x
x
Vy
Vz
My
Mz
P.L
P
F
-
-
-
-
F.L
Teniendoen cuenta elsignodelasFuerzasCortantes yMomentosFlectores:
0
(cte)
(cte)
.
0 0
.
.
0 0
.
y
z
y
y
y
z
z
z
x L
V F
V P
M P x
x M
x L M P L
M F x
x M
x L M F L
≤ ≤
= −
= −
= −
= → =
= → = −
= −
= → =
= → = −

8
Relaciones entre Fuerzas Cortantes y Momentos Flectores
Las Fuerzas Cortantes y los Momentos Flectores no son independientes sino que están
relacionados entre sí.
Antes de ver dicha relación conviene dejar claro que, en rigor, no existen fuerzas
concentradas en un punto, pues según se vio en 1.1, por el Principio de Saint Venant, se
podrán considerar concentradas las fuerzas que se transmitan a la barra a través de una
superficie pequeña en comparación con la superficie de ésta.
Se considera una rebanada de una viga formada por dos secciones muy próximas,
separadas dx y sobre la que actúa una carga distribuida q(x). En ambas caras de la
rebanada se sitúan las correspondientes Fuerzas Cortantes y Momentos Flectores (todos
con sentidos positivos)
Estableciendo las ecuaciones de equilibrio de los esfuerzos que actúan sobre la
rebanada:
“La Fuerza Cortante es la derivada del Momento Flector”
R
q(x) Kg/m
M+dM
V+dV
M
V
dx
n>0n<0 G
Fig.5.11
0 . . .
2
simplificando ydespreciandoinfinitésimosde2ºorden frentea losde1º:
.
G
dx
M M V dx M dM q dx
V dx dM
= + = + +
= →
∑
dM
V
dx
= )1.5(

Sección 5.2: Fuerzas Cortantes y Momentos Flectores. Diagramas y relaciones entre ellos
9
“la carga q(x) es la derivada de la Fuerza Cortante o la segunda derivada del Momento
Flector”
Observación: La expresión del Momento Flector es siempre de un grado superior a la de
la Fuerza Cortante
0 . simplificando : 0 .F V q dx V dV q dx dV= = + + = +∑
2
2
dV d M
q
dx dx
− = =
V
M
x
x
V=0
V=C1
V=C1.x+C2
M=C1.x+C2
V=C1.x2
+C2.x+C3
M=C1.x2
+C2.x+C3
M=C1.x3
+C2.x2
+C3.x+C4
M=C1
V=0
M=Mmax
( )
1
1 1 1 1 2
2
1 2 1 2 1 2 1 2 3
max min
0 0 ( )
. .
. . . . . .
0 ( 1 ) 0 ( 1 ) o
dM
V V M C cte
dx
dM
V C V C dM C dx M C x C
dx
dM
V C x C V C x C dM C x C dx M C x C x C
dx
dM
V en punto V en punto M
dx
= → = = → =
= → = = → = → = +
= + → = = + → = + → = + +
= → = = →
)2.5(

10
5.3.-FLEXIÓN PURA
5.3.1.-TENSIONES NORMALES: CASO GENERAL
Una viga está sometida a FLEXIÓN PURA cuando en sus secciones rectas
transversales actúan únicamente los Momentos Flectores Mz y/o My
Las relaciones tensiones – solicitaciones vistas en la sección 1.6 serían:
Pero al igual que ocurría en la Tracción-Compresión éstas ecuaciones, por si solas, no
permiten calcular las tensiones originadas por los Momentos Flectores Mz y/o My.
Habrá que recurrir nuevamente a hipótesis simplificativas que han sido comprobadas
experimentalmente.
Hipótesis de Bernouilli – Navier: “ En la Flexión Pura cada sección transversal de la
viga gira alrededor de un eje, contenido en la sección, denominado Eje Neutro,
permaneciendo las secciones planas y normales a las fibras deformadas”.
Admitiremos también que la flexión se produce en régimen elástico y por tanto dentro
de los límites de validez de la Ley de Hooke, por lo que las tensiones que se originan
han de ser proporcionales a las deformaciones producidas.
Mz
My
O
x
z
y
G
Fig.5.12
( )
0 . 0 . 0 .
0 . . . . . . .
x y xy z xz
A A A
xz xy y x z xA A A
N dA V dA V dA
T y z dA M z dA M y dA
σ τ τ
τ τ σ σ
= = = = = =
= = − = =
∫ ∫ ∫
∫ ∫ ∫
)3.5(

Sección 5.3.1: Flexión Pura. Tensiones normales: Caso general
11
Al flexionar la viga, las secciones transversales giran y hacen que las fibras
longitudinales, inicialmente rectas, dejen de serlo y se curven, alargándose o
acortándose según sea su posición en el interior de la viga.
Existen fibras longitudinales que ni se alargan ni se acortan, a esas fibras se las
denomina FIBRAS NEUTRAS.
A la superficie donde se encuentran las fibras neutras se la denomina SUPERFICIE
NEUTRA. Las fibras que estén por encima o por debajo de la Superficie Neutra
alargarán o acortarán según hacia donde flexione la viga. (En el caso del dibujo
acortarán las fibras que están por encima de la Superficie Neutra y alargarán las que
estén por debajo)
A las fibras transversales de la Superficie Neutra se las denomina: LINEAS NEUTRAS
o EJES NEUTROS. Alrededor de ellos giran las secciones transversales
En las siguientes figuras se representan estos términos para su mejor identificación:
Fibras que se acortan
Fig.5.13
Superficie Neutra
Ejes Neutros o
Líneas neutras
Fibras Neutras
Eje Neutro o
Línea Neutra
Fibras que se alargan
Fig.5.14

12
Así pues como resultado de la flexión el paralelepípedo elemental abcd se transforma
en el a1b1c1d1 y como según la Hipótesis de Bernouilli-Navier: “……las secciones
transversales de la viga giran alrededor de un eje, contenido en la sección, denominado
Eje Neutro, permaneciendo planas y normales a las fibras deformadas”, se deducirá
que: a1b1 será perpendicular a a1c1. Con lo cual se podrá afirmar: “Las deformaciones
angulares de los diferentes paralelepípedos son nulas, es decir: γ = 0”
Por la ley de Hooke:
“En la Flexión Pura son nulas las tensiones cortantes”
Para calcular las tensiones normales σx, se analizará con más detalle la deformación de
la rebanada dx de la figura anterior
Se estudiará el alargamiento que ha sufrido la fibra ab que se encuentra a una distancia
dn de la superficie neutra. La fibra ab de longitud dx al flexionar se ha convertido en la
fibra a1b1.
La fibra neutra mn de longitud dx al flexionar se ha convertido en la fibra m1n1 de la
misma longitud (la fibra neutra ni alarga ni acorta). Si se traza por n1 una paralela a
m1a1 se obtiene n1b2, siendo entonces: a1b2 =dx. El alargamiento de la fibra ab al
flexionar habrá sido: b2b1. A continuación se buscará una expresión para obtener dicho
alargamiento:
De la semejanza de triángulos (Oa1b1) y (n1b2b1), tienen
dx
m n
a b
c d
m1 n1
a1 b1
c1
d1
Fig.5.15
→== 0
G
τ
γ 0=τ
dx
m n
a b
c d
n1
m1
a1 b1
c1 d1
r
dn
dx
b2
dn
O
Supongamos que la superficie
neutra es la que pasa por la
fibra mn. (m1n1 una vez
flexionada)
O: Centro de curvatura de la
fibra neutra m1n1
r: radio de curvatura de la
fibra neutra m1n1
dx
bb
ba
bb
x
12
21
12
==ε
)4.5(

13
sus lados paralelos , se podrá expresar:
Sustituyendo en la expresión de εx:
“ las deformaciones longitudinales de las fibras son proporcionales a su distancia a
la superficie neutra”
y por la ley de Hooke:
“ las tensiones normales σσσσx son proporcionales a su distancia a la superficie
neutra”
Utilizando ahora la primera ecuación de las expresiones (5.3) resultará:
Si se quisiera obtener ahora la distancia del centro de gravedad de la sección a la
superficie neutra, la fórmula a emplear sería:
→
“la distancia del centro de gravedad G de una sección a la superficie neutra es
cero, el centro de gravedad está pues en la superficie neutra”, o lo que es lo mismo
“el eje neutro o línea neutra de una sección pasa por el centro de gravedad G de la
misma”
r
d
dx
bb n
=12
r
d
dx
bb n
x == 12
ε
)5.5(..
r
d
EE
E
n
xx
x
x ==→= εσ
σ
ε
. 0 . . 0 (alser E=cte, r=cte) . 0
. 0
n
x n
A A A
nA
d E
dA E dA d dA
r r
d dA
σ = → = → = →
→ =
∫ ∫ ∫
∫
. 0
( ) (y por loobtenidoantes) 0
nA
n
A A
d dA
d G
dA dA
= = = =
∫
∫ ∫
0)( =Gdn )6.5(
Eje Neutro o
Línea Neutra
G
Fig.5.16

14
Se buscará a continuación una forma cómoda para medir dn, Para ello, la siguiente
figura (5.17), representa una sección transversal cualquiera de una viga y se expresará
dn en función de las coordenadas del punto donde se quiera hallar la tensión.
La distancia dn de un punto P(y,z) cualquiera a la línea neutra será:
Introduciendo este valor en la ecuación (5.5) que da la tensión normal en un punto
cualquiera quedará:
Desarrollando ahora dos nuevas ecuaciones de las expresiones (5.3):
y resolviendo este sistema de ecuaciones por la regla de Cramer:
1 2
2
1 2 1 2
1 2
2
1 2 1 2
. . (ysegún 5.6) ( . . ). .
. . . . . . .
. . ( 5.6) ( . . ). .
. . . . . . .
z x
A A
z zyA A
y x
A A
zy yA A
M y dA C y C z y dA
C y dA C z y dA C I C I
M z dA y según C y C z z dA
C y z dA C z dA C I C I
σ
σ
= = = +
= + = +
= = = +
= + = +
∫ ∫
∫ ∫
∫ ∫
∫ ∫
G
z
y
P
α
n
n
y
z
dn
Línea neutra o Eje neutro
Fig.5.17
zCyCsenzy
r
E
r
d
E n
x ..).cos..(. 21 +=+== αασ
αα senzydn .cos. +=
)7.5(

15
Sustituyendo finalmente el valor obtenido para las dos constantes C1 y C2 en la ecuación
(5.7), quedará como expresión final general del cálculo de la tensión normal en un
punto cualquiera de coordenadas (y,z) la siguiente:
Las componentes del estado de tensiones en un punto P del interior de una viga
sometida a Flexión Pura serán pues:
)8.5(
21
.
..
zyyz
zyyyz
yzy
zyz
yy
zyz
III
IMIM
II
II
IM
IM
C
−
−
== 22
.
..
zyyz
zyzzy
yzy
zyz
yzy
zz
III
IMIM
II
II
MI
MI
C
−
−
==
2
.
)...()...(
zyyz
zyzzyzyyyz
x
III
zIMIMyIMIM
−
−+−
=σ
00
00
0
.
)...()...(
2
==
==
=
−
−+−
=
zxz
yzy
xy
zyyz
zyzzyzyyyz
x
III
zIMIMyIMIM
τσ
τσ
τσ
)9.5(
P
σxσx x
z
y Fig.5.18

16
CÁLCULO DE LA LÍNEA NEUTRA (EJE NEUTRO)
Las fibras que pertenecen a la Superficie Neutra, por definición, ni se alargan ni se
acortan, con lo cual se cumplirá:
Así pues la ecuación de la línea neutra la podemos obtener como lugar geométrico de
los puntos de una sección que tienen tensión normal cero, es decir:
o lo que es lo mismo:
Ecuación de la línea neutra o Eje neutro
También puede expresarse, sabiendo que ha de pasar por el centro de gravedad G de la
sección, en virtud de (5.6), por su ángulo de inclinación α con respecto al eje z.
Ángulo de inclinación de la línea neutra respecto al eje Z
0 y por la leyde Hooke : . 0x x x Eε σ ε= = =
0
.
)...()...(
2
=
−
−+−
=
zyyz
zyzzyzyyyz
x
III
zIMIMyIMIM
σ
0)...()...( =−+− zIMIMyIMIM zyzzyzyyyz
)10.5(
)11.5(
. .
(despejandoesta expresionde5.10)
. .
y z z zy
z y y zy
M I M Iy
tag
z M I M I
α
−
= = = −
−
G
z
y
α
n
n
Fig.5.19
Sección transversal de la viga

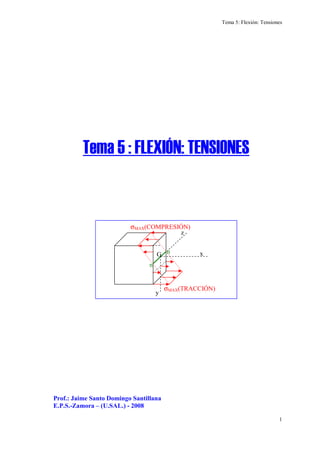
Tema 5.3.2: Tensiones normales: Casos particulares
17
5.3.2.-TENSIONES NORMALES: CASOS PARTICULARES
Caso Particular 1º: “Los ejes y,z son los Ejes Principales de inercia de la sección”
En éste caso se deberá cumplir: Izy = 0, con lo cual las ecuaciones 5.8 y 5.11 serán:
Caso Particular 2º: “Los ejes y,z son los Ejes Principales de inercia de la sección y
además uno de los Momentos Flectores es cero”
Si My = 0 :
La distribución de tensiones normales σx para este caso será:
y
y
z
z
x
I
zM
I
yM ..
+=σ )12.5(
yz
zy
IM
IM
tag
.
.
−=α )13.5(
z
z
x
I
yM .
=σ )14.5(
0 0º
elejeneutroeselejez
tagα α= → =
)15.5(
G x
z
y
n
n
σMAX(COMPRESIÓN)
σMAX(TRACCIÓN)
Fig.5.20
max
.z MAX
X
z
M y
I
σ = )16.5(

Tema 5 : Flexión: tensiones
18
Si Mz = 0 :
La distribución de tensiones normales σx para este caso será:
y
y
x
I
zM .
=σ )17.5(
90º
elejeneutroeseleje y
tagα α= ∞ → =
)18.5(
G x
z
y
n
n
σMAX(COMPRESIÓN)
σMAX(TRACCIÓN)
Fig.5.21
max
.y MAX
X
y
M z
I
σ = )19.5(

Tema 5.3.2: Tensiones normales: Casos particulares
19
Observaciones:
Convenio de signos para Mz y My:
Con el convenio de signos adoptado en la sección 5.2 para los Momentos flectores Mz y
My se observa lo siguiente:
Mz > 0 → “las fibras que se alargan son las que están por debajo de la superficie
neutra, por tanto se producirá TRACCIÖN en los puntos de la sección de la parte
inferior del eje z, es decir en los puntos de la parte positiva del eje y”
My > 0 → “las fibras que se alargan son las que están en la parte positiva del eje z”
n > 0
Mz
Mz
x
z
y
G
y
znn G
Tracción
Compresión
n
n n
n
Superficie neutra
Fig.5.22
x
n > 0
My
My
z
y
n
n
n
n
Superficie neutra
G
Compresión
n
y
z
n
Tracción
Fig.5.23

Tema 5 : Flexión: tensiones
20
5.3.3.-LÍNEA ELÁSTICA. RADIO DE CURVATURA
Se denomina LÍNEA ELÁSTICA al eje x de la viga una vez deformado debido a la
flexión.
El radio de curvatura de la línea elástica se podrá obtener de la siguiente manera:
La ecuación 5.5 que daba la tensión en un punto P cualquiera:
y para el 2º caso particular visto en 5.3.2: ( Izy = 0 My = 0 ) → el eje neutro es el eje z
Entonces : dn = y, con lo cual la fórmula de la tensión será:
La fórmula final (5.14), para el cálculo de la tensión en éste caso particular era:
Igualando ambas expresiones de la tensión:
Siendo: E.Iz = Módulo de Rigidez a la flexión alrededor del eje z.
así si:
1
. flexa poco,esmuy rígida a la flexiónzE I r
r
↑ → ↓ → ↑ ⇒
x
x
Línea elástica
Fig.5.24
G
z
y
P
α
n
n
y
z
dn
Fig.5.25
r
d
E n
x .=σ
G
z
y
P
nn
dn = y
r
y
Ex .=σ
z
z
x
I
yM .
=σ
z
z
IE
M
r .
1
=→=
z
z
I
yM
r
yE .. )20.5(

Sección 5.3.3: Línea elástica. Radio de curvatura
21
Para el otro caso particular visto en 5.3.2: ( Izy = 0, Mz = 0 ) → el eje neutro es el eje
y, entonces dn = z.
Con lo cual la ecuación (5.5) para la tensión sería:
La ecuación final (5.17), para el cálculo de la tensión en éste caso particular era:
Igualando ambas expresiones de la tensión:
Siendo: E.Iy = Módulo de Rigidez a la flexión alrededor del eje y.
G
z
y
P
n
n
dn = z
Fig.5.26
r
z
Ex .=σ
y
y
x
I
zM .
=σ
→=
y
y
I
zM
r
zE ..
y
y
IE
M
r .
1
= )21.5(
E.Iz (pequeño)
⇓
Flexiona mucho
⇓
poco rígida a la flexión
E.Iz (grande)
⇓
Flexiona poco
⇓
muy rígida a la flexión

22
5.4.-FLEXIÓN SIMPLE
Una viga está solicitada a FLEXIÓN SIMPLE cuando en sus secciones transversales actúan
conjuntamente los Momentos Flectores: Mz y/o My y las Fuerzas Cortantes: Vy y/o Vz.
Las relaciones Tensiones – Solicitaciones vistas en 1.7 serían:
5.4.1-TENSIONES NORMALES
En estas ecuaciones (5.22), se observa que en las relaciones que interviene la tensión normal
σx, son las mismas que las expresadas en las (5.3) para la Flexión Pura. Sin embargo la
aparición ahora de las tensiones cortantes: τxy y τxz , que eran cero en la Flexión Pura, va a
producir deformaciones angulares γ, que habrá que añadir a las deformaciones propias de la
Flexión Pura.
Si las tensiones cortantes no se distribuyeran uniformemente en la sección, lo mismo ocurriría
con las deformaciones angulares, lo que significará que en la FLEXIÓN SIMPLE las
secciones planas se alabean, es decir, no permanecerán planas y no se cumplirá por tanto la
Hipótesis de Bernouilli- Navier
Vz
Vy
Mz
My
x
y
z
O G
Fig.5.27
( )
0 . . .
0 . . . . . . .
x y xy z xz
A A A
xz xy y x z xA A A
N dA V dA V dA
T y z dA M z dA M y dA
σ τ τ
τ τ σ σ
= = = =
= = − = =
∫ ∫ ∫
∫ ∫ ∫
)22.5(
Fibras que se acortan
Fibras que se alargan
Fig.5.28

Sección 5.4.1: Flexión simple: tensiones normales
23
Sin embargo se comprueba, que este alabeo de las secciones apenas influye en el valor de las
tensiones normales σx, con lo cual se aplicará para éstas, en el caso de FLEXIÓN SIMPLE,
las mismas ecuaciones obtenidas en la FLEXIÓN PURA, es decir:
Caso Particular 1º:
“Los ejes y,z son los Ejes Principales de inercia de la sección”
“Los ejes y,z son los Ejes Principales de inercia de la sección y además uno de los Momentos
Flectores es cero”
Si My = 0 :
0
0
.
)...()...(
2
=
=
−
−+−
=
z
y
zyyz
zyzzyzyyyz
x
III
zIMIMyIMIM
σ
σ
σ
y
y
z
z
x
I
zM
I
yM ..
+=σ )12.5(
yz
zy
IM
IM
tag
.
.
−=α )13.5(
z
z
x
I
yM .
=σ )14.5( zejeelesneutroejeel
tag º00 =→= αα
)15.5(
(5.7)

24
5.4.2-TENSIONES CORTANTES EN SECCIONES DE GRAN ESPESOR
Para el cálculo de las tensiones cortantes se tendrá en cuenta la forma de la sección de la viga.
Así en este apartado se comenzará con el caso de vigas con secciones de gran espesor:
circulares, rectangulares, etc…..
En este tipo de secciones se hará el cálculo por separado de las tensiones cortantes: τxy y τxz.
Cálculo de la tensión cortante ττττxy:
Tomemos una rebanada dx de una viga de sección de gran espesor sometida a Flexión Simple
(Fig.29.a). En ambos extremos de la misma se sitúan los Momentos Flectores y Fuerzas
Cortantes correspondientes. Se trata de calcular las τxy en los puntos de una línea cualquiera
ab que se encuentran a una distancia y del eje z. Para ello se supondrá que τxy = cte a lo largo
de todos los puntos de la dicha línea.
Seccionando el elemento diferencial por el plano abcd y estableciendo el equilibrio de fuerzas
del trozo inferior resultante, se tendrá:
Vz + dVz
Vy + dVy
Mz + dMz
My + dMy
x
y
z
O G
n>0
My
Mz
Vy
Vz
n<0
τxy
y
a
b c
d
dx
Fig.5.29.a
a
b c
dσx σx +dσx
t(y)
τyx
dA dA
A
Fig.29.b
dx
( )
, ,
y para queexista equilibriodefuerzasen direccion delejex sobresuperficieabcd
0 . . . ( ). yoperando :
z y x z z y y x x
yx
x x x x yx
A A
M M M dM M dM d
F d dA dA t y dx
σ σ σ
τ
σ σ σ τ
→ + + → +
→
= → + = +∑ ∫ ∫

Sección 5.4.2: Tensiones cortantes en secciones de gran espesor
25
y como por lo visto en el tema 1º : τyx = τxy se obtendrá finalmente:
siendo:
Observación: en la sección de n>0 se cumple:
. . ( ). . . ( ) (1)
Calculemos a partir de la expresión de obtenida en (5.7):
x
x yx yxA A
x
x
d
d dA t y dx dA t y
dx
d
dx
σ
σ τ τ
σ
σ
= → =∫ ∫
( ) ( )
2 2
2 2
( . . ). ( . . ). .( . . ) .( . . )
. .
. . . . . . .( . . ) .( . . )
. .
ysustituyendoesta expr
z y y zy y z z zy z y zy y z zy
x
z y zy z y zy
yz
y zy z zy
y y zy z z zyx
z y zy z y zy
M I M I y M I M I z M I y I z M I z I y
I I I I I I
dMdM
I y I z I z I y V I y I z V I z I yd dx dx
dx I I I I I I
σ
σ
− + − − + −
= =
− −
− + − − + −
= =
− −
( ) ( )
2
2
esión en (1):
. . . . . .
. ( ) .
.
. . . . . . . . . .
. ( )
.
y y zy z z zy
yx A
z y zy
y y zy z z zy
A A A A
yx
z y zy
V I y I z V I z I y
t y dA
I I I
V I y dA I z dA V I z dA I y dA
t y
I I I
τ
τ
− + −
=
−
   − + −
   =
−
∫
∫ ∫ ∫ ∫
2
. . ( ) . ( ) . . ( ) . ( )
( ). .
y y z zy y z z y zy z
yx
z y zy
V I Q y I Q y V I Q y I Q y
t y I I I
τ
   − + −   =
 − 
2
. . ( ) . ( ) . . ( ) . ( )
( ). .
xy
z y zy
V I Q y I Q y V I Q y I Q y
t y I I I
τ
   − + −   =
 − 
)23.5(
∫∫ ==
A
y
A
z dAzyQdAyyQ .)(.)(
y
y
z
t(y)
G
a b
Fig.5.30
τxy>0 A
losmomentosestáticosdelárea rayada A
respectodelosejesze yrespectivamente
0 "susentidoesentranteen elárea rayada"
0 "su sentidoessalientedelárea rayada"
xy
xy
τ
τ
> →
< →

26
Cálculo de la tensión cortante ττττxz:
Se trata de calcular ahora las τxz en los puntos de una línea cualquiera ef que se encuentran a
una distancia z del eje y. Para ello se supondrá que τxz = cte a lo largo de todos los puntos de
la dicha línea.
Seccionando el elemento diferencial por el plano efgh y estableciendo el equilibrio de fuerzas
del trozo posterior resultante, se tendrá:
dx
t(z)
dAdAσx σx + dσxτzx
e h
gf
A
Fig.5.31.b
( )
, ,
ypara queexista equilibriodefuerzasendireccion deleje x sobresuperficieefgh
0 . . . ( ). yoperando:
z y x z z y y x x
zx
x x x x zx
A A
M M M dM M dM d
F d dA dA t z dx
σ σ σ
τ
σ σ σ τ
→ + + → +
→
= → + = +∑ ∫ ∫
. . ( ). . . ( )
ysiguiendoun procesosimilaralanterior,seobtendrá:
x
x zx zxA A
d
d dA b z dx dA t z
dx
σ
σ τ τ= → =∫ ∫
2
. . ( ) . ( ) . . ( ) . ( )
( ). .
xz
z y zy
V I Q z I Q z V I Q z I Q z
t z I I I
τ
   − + −   =
 − 
)24.5(
Vz + dVz
Vy + dVy
Mz + dMz
My + dMy
x
y
z
O G
n>0
My
Mz
Vy
Vz
n<0
τxz
z
e
f
h
g
dx Fig.5.31.a

Sección 5.4.2: Tensiones cortantes en secciones de gran espesor
27
siendo:
CASOS PARTICULARES:
“Los ejes y,z son los Ejes Principales de inercia de la sección y además una de las Fuerzas
Cortantes es cero”
-si Vz = 0 →
- si Vy = 0 →
A
z
y
z
G
e
t(z)
f
Fig.5.32
τxz>0 ∫∫ ==
A
y
A
z dAzzQdAyzQ .)(.)(
. ( ) . ( )
( ). ( ).
y z z y
xz
z y
V Q z V Q z
t z I t z I
τ = +
. ( ) . ( )
( ). ( ).
y z z y
xy
z y
V Q y V Q y
t y I t y I
τ = +
. ( )
( ).
y z
xy
z
V Q y
t y I
τ =
. ( )
( ).
y z
xz
z
V Q z
t z I
τ =
. ( )
( ).
z y
xy
y
V Q y
t y I
τ =
. ( )
( ).
z y
xz
y
V Q z
t z I
τ =
(5.25)
(5.26)
(5.27)
0 "su sentidoesentranteen elárea rayada"
0 "su sentidoessalientedelárea rayada"
xz
xz
τ
τ
> →
< →

28
5.4.3-TENSIONES CORTANTES EN SECCIONES ABIERTAS DE PEQUEÑO
ESPESOR
Las barras que se utilizan en las estructuras metálicas suelen tener secciones de pequeño
espesor.
Se consideran incluidas en este grupo todas las secciones en las que se cumpla:
El cálculo de las tensiones cortantes en este tipo de secciones, presenta algunas diferencias
con respecto al de las secciones macizas visto anteriormente.
Cálculo de la tensión cortante ττττxs:
Tomemos una rebanada dx de una viga de sección abierta de pequeño espesor sometida a
Flexión Simple. En ambos extremos de la misma se sitúan los Momentos Flectores y Fuerzas
Cortantes correspondientes. Se trata de calcular las τxs en los puntos de una línea cualquiera
ab, perpendicular a la línea media, que se encuentran a una distancia s de uno de los extremos
abiertos de la sección. Para ello se supondrá que τxs = cte a lo largo de todos los puntos de
dicha línea y sus direcciones son perpendiculares a la misma
h h
b b
tw
tw
tf tf
Fig.5.33
dd
10. 10.w fh t b t≥ ≥
Vy
Vz
My
Mz
y
x
z
G
s
Vy+dVy
Vz+dVz
My+dMy
Mz+dMz
n>0
n<0
dx
a
b cτxs
Fig.5.34.a

Sección 5.4.3: Tensiones cortantes en secciones abiertas de pequeño espesor
29
Seccionando el elemento diferencial por el plano abcd y estableciendo el equilibrio de fuerzas
en dirección del eje x, del trozo inferior resultante, se tendrá:
y siguiendo a partir de ahora un desarrollo similar al realizado en el cálculo de las tensiones
cortantes en secciones de gran espesor, se obtendrá:
siendo:
s
dx
a
b c
d
σx
σx+dσx
τsx
t(s)
dA
Fig.5.34.b
( )0 . . . ( ). yoperando:x x x x sxA A
F d dA dA t s dxσ σ σ τ= → + = +∑ ∫ ∫
. . ( ). . . ( )x
x sx sxA A
d
d dA t s dx dA t s
dx
σ
σ τ τ= → =∫ ∫
2
. . ( ) . ( ) . . ( ) . ( )
( ). .
xs
z y zy
V I Q s I Q s V I Q s I Q s
t s I I I
τ
   − + −   =
 − 
(5.28)
a
b
s
y
zG
A
Fig.5.34.c
τxs>0
∫∫ ==
A
y
A
z dAzsQdAysQ .)(.)(
0 "su sentidoesentranteen elárea rayada"
0 "susentidoessalientedelárea rayada"
xs
xs
τ
τ
> →
< →

30
CASOS PARTICULARES:
En éste caso se deberá cumplir: Izy = 0, con lo cual la ecuación 5.28 será:
“Los ejes y,z son los Ejes Principales de inercia de la sección y además una de las Fuerzas
Cortantes es cero”
-si Vz = 0 →
- si Vy = 0 →
. ( ) . ( )
( ). ( ).
y z z y
xs
z y
V Q s V Q s
t s I t s I
τ = + (5.29)
. ( )
( ).
y z
xs
z
V Q s
t s I
τ =
. ( )
( ).
z y
xs
y
V Q s
t s I
τ =
(5.30)
(5.31)

Sección 5.4.4: Tensiones cortantes en secciones cerradas de pequeño espesor
31
5.4.4-TENSIONES CORTANTES EN SECCIONES CERRADAS DE PEQUEÑO
ESPESOR
Cálculo de la tensión cortante ττττxs:
Tomemos una rebanada dx de una viga de sección cerrada de pequeño espesor sometida a
Flexión Simple. En ambos extremos de la misma se sitúan los Momentos Flectores y Fuerzas
Cortantes correspondientes. Se trata de calcular las τxs en los puntos de una línea cualquiera
ab, perpendicular a la línea media, que se encuentran a una distancia s de una línea aobo,
también perpendicular a la línea media, que se tomará como referencia. Para ello se supondrá
que τxs = cte a lo largo de todos los puntos de la línea ab, de espesor t(s), siendo sus
direcciones perpendiculares a la misma y que igualmente ocurrirá con las tensiones τxso = cte
en los puntos de la línea de referencia aob, de espesor t(so)
Seccionando el elemento diferencial por el plano abcd y por el aobocodo, y estableciendo el
equilibrio de fuerzas en dirección del eje x, del trozo resultante, se tendrá:
y sustituyendo el valor de dA
dx
d
A
x
.∫
σ
obtenido en la sección 5.4.3:
My
Vz
Mz
Vy+dVy
Vz+dVz
My+dMy
Mz+dMz
xG n>0n<0
s τxso
τxs
y
z
a
b
a0
b0
Fig.5.35.a
Vy
dx
a
a0
b
b0
s
dx
σx
σx+dσx
τsx
τsox
t(s)
c
d
co
do
t(so)
dA
Fig.5.35.b
( )0 . . ( ). . . ( ).x x x sox o x sxA A
F d dA t s dx dA t s dxσ σ τ σ τ= → + + = +∑ ∫ ∫
.. . ( ). . ( ).x sox o sxA
d dA t s dx t s dxσ τ τ+ = →∫ )(.)(... sesedA
dx
d
sxosox
A
x
ττ
σ
=+∫

32
Observación: en esta expresión se observa que para poder calcular τsx se deberá antes conocer
τsox. Ésto no ocurría en las secciones abiertas de pequeño espesor, pues en ellas tan sólo era
necesario dar un corte para aislar el elemento diferencial y estudiar sobre él, el equilibrio de
fuerzas, con lo cual se obtenía una ecuación con una sola incógnita: τsx, y se la podía calcular
directamente.
Cálculo de una tensión de referencia: τsox
El cálculo de una tensión de referencia τsox se obtiene a partir de la siguiente propiedad: “la
suma de las deformaciones angulares γxs a lo largo de toda la línea media de una sección
cerrada de pequeño espesor es cero”
y sustituyendo τxs =τsx por su valor obtenido de la ecuación (5.32):
0 0
. 0 ypor la leydeHooke : . 0
s s
xs
xs ds ds
G
τ
γ = → =∫ ∫
2
0 0
. . ( ) . ( ) . . ( ) . ( ). ( )
. . 0
( ). ( ). .( . )
como : cte, ( ) cte y eliminando G :
s s
y y z zy y z z y zy zsox o
y z zy
sox o
V I Q s I Q s V I Q s I Q st s
ds ds
t s G t s G I I I
t s
τ
τ
   − + −   + =
−
= =
∫ ∫
2
0 0
. . ( ) . ( ) . . ( ) . ( )
. ( ). . 0
( ) ( ).( . )
y despejando finalmente :
s s
sox o
y z zy
sox
V I Q s I Q s V I Q s I Q sds
t s ds
t s t s I I I
τ
τ
   − + −   + =
−∫ ∫
0 0 0 0
2
0
0
( ) ( )( ) ( )
. . . . . . . . . .
( ) ( ) ( ) ( )
( ).( . )
( )
s s s s
y yz z
y y zy z z zy
z y zy
sox xsos
Q s Q sQ s Q s
V I ds I ds V I ds I ds
t s t s t s t s
t s I I I
ds
t s
τ τ
   
− + −   
   −
−
= =
∫ ∫ ∫ ∫
∫
(5.33)
2
. . ( ) . ( ) . . ( ) . ( )
. ( ) . ( ) (5.32)
.
sx sox o
z y zy
V I Q s I Q s V I Q s I Q s
t s t s
I I I
τ τ
   − + −   = +
−

Sección 5.4.4: Tensiones cortantes en secciones cerradas de pequeño espesor
33
Una vez obtenida de esta forma τsox, sustituyendo su valor en la ecuación (5.33) se obtendría
el valor de la tensión que se quería calcular: τxs = τsx
CASOS PARTICULARES:
Caso Particular 1º: “Los ejes y,z son los Ejes Principales de inercia de la sección”
Caso Particular 2º: “Los ejes y,z son los Ejes Principales de inercia de la sección y además
una de las Fuerzas Cortantes es cero”
Por ejemplo: caso de Vz = 0
0
2
. . ( ) . ( ) . . ( ) . ( ). ( )
( ) ( ).( . )
y y z zy y z z y zy zxso
xs
z y zy
V I Q s I Q s V I Q s I Q st s
t s t s I I I
τ
τ
   − + −   = +
−
(5.34)
0 0
0 0
0
( )( )
. . . .
( ) ( )
( ). ( ).
( )
s s
yz
y z
z y
xso s
Q sQ s
V ds V ds
t s t s
t s I t s I
ds
t s
τ
+
= −
∫ ∫
∫
(5.37)
0
. ( ) . ( ). ( )
( ) ( ). ( ).
y z z yxso
xs
z y
V Q s V Q st s
t s t s I t s I
τ
τ = + + (5.36)
(5.35)
0
0
0
( )
. .
( )
( ).
( )
s
z
y
z
xso s
Q s
V ds
t s
t s I
ds
t s
τ = −
∫
∫
0
. ( ). ( )
( ) ( ).
y zxso
xs
z
V Q st s
t s t s I
τ
τ = + (5.38)

34
“Si el eje y es de simetría y sólo hay Vy”
En este caso las ecuaciones anteriores se simplifican, pues se demuestra que en los puntos de
corte de la sección con el eje y la tensión cortante es cero.
Así pues tomando dichos puntos como referencia, en ellos será:
con lo cual la tensión cortante en cualquier otros puntos será:
siendo Qz(s) el momento estático del área rayada respecto del eje z
Fórmulas análogas se obtendrían si el eje z fuese de simetría y sólo hubiese Vz
Y finalmente si ambos ejes: y, z, fuesen de simetría y hubiese Vy y Vz, las fórmulas se
obtendrían por el Principio de Superposición de los Efectos, estudiando cada caso por
separado y sumando los valores obtenidos en ambos.
τxso =0
. ( )
( ).
y z
xs
z
V Q s
t s I
τ = (5.40)
Vy
y
z
τxs
τxso = 0
τxso = 0
Fig.5.36
(5.39)

Sección 5.4.5: Centro de fuerzas cortantes
35
5.4.5-CENTRO DE FUERZAS CORTANTES
Sea una viga con sección abierta de pequeño espesor y sea F la Resultante de las fuerzas
exteriores aplicada en el punto G de la sección indicada en la Fig. (5.37). La fuerza cortante
en dicha sección será pues: Vy = F
La distribución de tensiones cortantes τxs en las alas y en el alma de la sección, aplicando la
ecuación (5.30) será la indicada en la Fig. (5.38.a):
La suma de las tensiones cortantes en el alma τxs = τxy dará lugar a una resultante que será Vy,
y las de las alas: τxs = τxz, darán lugar a unas resultantes Vz. (Fig.5.38.b).
Llevando la acción de estas resultantes de las fuerzas interiores: Vy y Vz, al centro de
gravedad G de la sección, darán lugar a una Resultante: Vy (la suma de las Vz será cero, al
ser iguales, de la misma dirección, pero de sentidos contrarios), y un Momento Resultante:
Mx = Vz.h + Vy.c que produce una Torsión en la sección (Fig. 5.38.c)
z
y
G
Vext = F
Vy = Rint = F
x
Fig.5.37
z
y
G
Vy
Vz
Fig.5.38.b.
h
c
Vz
z
y
G
Vy
Mx = Vz.h + Vy.c
Fig.5.38.c
z
y
G
τxs = τxz
τxs = τxz
τxs = τxy
Vy
Fig.5.38.a
⇒

36
Este efecto inesperado de la Torsión que producen las tensiones cortantes y al que tan
sensibles son este tipo de secciones abiertas y de pequeño espesor (tienen muy poca rigidez a
la torsión), se podrá evitar si se aplican las fuerzas exteriores, en lugar de en el centro de
gravedad G de la sección, en un punto C al que llamaremos “Centro de Fuerzas Cortantes”.
Calculemos a continuación la posición del Centro de Cortantes ( C ), para la sección dada.
Para ello se situarán las fuerzas exteriores que actúen sobre la viga, de modo que la Resultante
de las mismas pase por un punto C sobre el eje z y a una distancia d del centro de gravedad G
de la sección. (Fig.5.39.a). Para ver el efecto que dicha Resultante provoca en G, la
trasladamos a dicho punto, dando lugar a una fuerza: F y un momento: F.d. (Fig. 5.39.b)
Pero al estar la Resultante de las fuerzas exteriores F, aplicada ahora en el punto G, (Fig.
5.39.b) , F, esta fuerza sólo, por lo visto anteriormente, provocará unas fuerzas internas que
daban lugar a la fuerza y al momento indicados (Figs.5.40.a y b)
Si situamos el punto C a una distancia d del punto G, tal que se consiga que el momento
torsor exterior: Mx, sea igual y de sentido contrario al provocado por las fuerzas internas: Mx ,
se habrá conseguido anular éstas, es decir se habrá anulado el efecto de la Torsión en la
sección
⇒
con ello queda localizada la posición del punto C (Centro de fuerzas cortantes), para este tipo
de sección
z
y
GC
d
Vext = F
Fig.5.39.a
⇒ z
y
GC
d
Fig.5.39.b
b
Vext = F
Mx = F.d
z
y
G
Vext = F
Vy = Rint = F
x
Fig.5.40.a
z
y
G
Ry
Mx = Vz.h + Vy.c
Fig.5.40.b
⇒
F.d = Vz.h + Vy.c
. .z yV h V c
d
F
+
= (5.41)

Sección 5.4.5: Centro de fuerzas cortantes
37
Observaciones:
Para otros tipos de secciones, los Centros de Cortantes serán:
a) Secciones abiertas de pequeño espesor con dos ejes de simetría
b) Secciones abiertas de pequeño espesor con sólo un eje de simetría
c) Secciones abiertas de pequeño espesor sin ejes de simetría
z
y
C ≡ G
Fig.5.43
z
y
C ≡ G
Fig.5.41
z
y
G
C
Fig.5.42.b
z
y
GC
d
Fig.5.42.a
z
y
C
G
Fig.5.42.c

38
5.5-INTRODUCCIÓN AL DIMENSIONAMIENTO A RESISTENCIA DE VIGAS
METÁLICAS SOLICITADAS A FLEXIÓN ( Normativa DB-SE-A )
5.5.1.-RESISTENCIA DE LAS SECCIONES A FLEXIÓN PURA: MOMENTOS
FLECTORES
1.-Criterio elástico de dimensionamiento:
Según vimos en la sección 3.7: “La resistencia elástica de una sección se obtendrá cuando en
un punto de la misma se alcance la tensión del límite elástico fy.”
Caso de una sección solicitada por un momento flector Mz:
Al momento flector Mz que produce la tensión del límite elástico fyd en los puntos más
alejados de la línea neutra, se le denomina: Mzel,d y representa la resistencia elástica de una
sección a la flexión Mz.. Calculemos su valor:
La distribución de tensiones normales σx para este caso será, (ver fig.5.44):
Así pues para la comprobación a resistencia elástica de una sección trabajando a Flexión Pura:
Mz, se aplicará la fórmula:
Mz
*
(carga mayorada) = Mz.γ :
G x
z
y
n
n
σMAX(COMPRESIÓN) = fyd
σMAX(TRACCIÓN) = fyd
Fig.5.44
Mz = Mzel,d
, , ,
max
.zel d MAX zel d zel d
X yd
zz zel
MAX
M y M M
f
II W
y
σ = = = = →
*
, .z zel d zel ydM M W f≤ =
, .zel d zel ydM W f= (5.42)
, z
z
max
siendo:
:"resistencia elástica de la sección a la flexión M "
:"módulo resistente elástico a la flexión M "
zel d
z
zel
M
I
W
y
=
(5.43)

Sección 5.5: Introducción al dimensionamiento a resistencia de vigas metálicas solicitadas a flexión
39
Mz: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
γ : coeficiente de seguridad para las cargas, (ver tabla 3.2)
Caso de una sección solicitada por un momento flector My:
De forma similar al caso anterior llegaríamos a los siguientes resultados:
La distribución de tensiones normales σx para este caso será ahora (ver fij.5.45):
Así pues para la comprobación a resistencia elástica de una sección trabajando a Flexión Pura:
My, se aplicará la fórmula:
My
*
(carga mayorada) = My.γ
My: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
Observación: Los módulos resistentes elásticos Wzel, Wyel, para el caso de series de perfiles
normalizados se pueden obtener en las tablas correspondientes a los mismos. En caso de
perfiles no normalizados se obtendrán a partir de sus expresiones respectivas..
Caso de los Momentos Flectores: Mz y My actuando simultáneamente:
En este caso la normativa propone la siguiente fórmula de cálculo:
G x
z
y
n
n
My = Myel,d
Fig.5.45
*
, .y yel d yel ydM M W f≤ =
**
, ,
1yz
zel d yel d
MM
M M
+ ≤
, , ,
max
.yel d MAX yel d yel d
X yd
yy yel
MAX
M z M M
f
II W
z
σ = = = = → , .yel d yel ydM W f= (5.44)
, y
y
max
siendo:
:"resistencia elástica de la sección a la flexión M "
:"módulo resistente elástico a la flexión M "
yel d
y
yel
M
I
W
z
=
(5.45)
(5.46)

40
2.-Criterio plástico de dimensionamiento:
Según vimos en la sección 3.7: “La resistencia plástica de una sección se obtendrá cuando en
todos los puntos de la misma se alcance la tensión del límite elástico fy.”
Caso de una sección solicitada por un momento flector Mz:
Al momento flector Mz que produce la tensión del límite elástico fyd en todos puntos de la
sección, se le denomina: Mzpl,d y representa la resistencia plástica de una sección a la flexión
Mz. Calculemos su valor:
Para obtener la resistencia plástica Mzpl,d de la sección se procederá del siguiente modo:
Así pues para la comprobación a resistencia plástica de una sección trabajando a Flexión
Pura: Mz, se aplicará la fórmula:
Mz
*
(carga mayorada) = Mz.γ :
Mz: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
G x
z
y
n
n
σ(COMPRESIÓN) = fyd
σ (TRACCIÓN) = fyd
Mz = Mzpl,d
Fig.5.46
,
/2
0 . . (como = = cte) . .
.2. . .
G zpl d yd yd
A A
yd zpl yd
A
M M dA y f f y dA
f y dA W f
σ σ= → = = = =
= =
∑ ∫ ∫
∫
*
, .z zpl d zpl ydM M W f≤ =
, .zpl d zpl ydM W f= (5.47)
, z
z
/ 2
siendo:
:"resistencia plástica de la sección a la flexión M "
2. . :"módulo resistente plástico a la flexión M "
zpl d
zpl
A
M
W y dA= ∫
(5.48)

41
Caso de una sección solicitada por un momento flector My:
De forma similar al caso anterior llegaríamos a los siguientes resultados:
Para obtener la resistencia plástica Mypl,d de la sección se procederá del siguiente modo:
Así pues para la comprobación a resistencia plástica de una sección trabajando a Flexión
Pura: My, se aplicará la fórmula:
My
*
(carga mayorada) = My.γ :
My: momento flector que solicita a la sección, que se obtiene de los diagramas de esfuerzos
En este caso la normativa propone la siguiente fórmula de cálculo:
G x
z
y
n
n
My = Mypl,d
Fig.5.47
*
, .y ypl d ypl ydM M W f≤ =
**
, ,
1yz
zpl d ypl d
MM
M M
+ ≤
,
/2
0 . . (como = = cte) . .
.2. . .
G ypl d yd yd
A A
yd ypl yd
A
M M dA z f f z dA
f z dA W f
σ σ= → = = = =
= =
∑ ∫ ∫
∫
, .ypl d ypl ydM W f= (5.49)
(5.50)
(5.51)
, y
y
/ 2
siendo:
:"resistencia plástica de la sección a la flexión M "
2. . :"módulo resistente plástico a la flexión M "
ypl d
ypl
A
M
W z dA= ∫

42
Observación: Los módulos resistentes plásticos Wzpl, Wypl, al igual que los elásticos, se
obtendrán: En el caso de series de perfiles normalizados, en las tablas correspondientes a los
mismos y en el caso de perfiles no normalizados, a partir de las expresiones respectivas
obtenidas para los mismos.
Ejemplo 1: Sección rectangular
Ejemplo 2: Sección circular
Ejemplo 3: IPE-300
z
y
b
h G
3 3
2 2
max max
2
( / 2) ( / 2)
/2
2
( / 2) ( /2)/ 2
. .
. .12 12
6 6
2 2
. .
2. . 2. . 2. .
4 2 4
. .
2. . 2. . 2. .
4 2 4
yz
zel yel
zpl G A A
A
ypl G A AA
b h hb
II b h h b
W W
h by z
h b h b h
W y dA y A
b b h h b
W z dA z A
= = = = = =
= = = =
= = = =
∫
∫
3
3
3
3
(tablas) 557,1mm
(tablas) 80,5 mm
(tablas) 628,4 mm
(tablas) 125,2 mm
zel
yel
zpl
ypl
W
W
W
W
= =
= =
= =
= =
z
y
R
4
3
max
2
3
( / 2) ( / 2)
/2
.
.4
4
(porsimetría)
4. . 4
2. . 2. . 2. . .
3. 2 3
(porsimetria)
z
zel
yel zel
zpl G A A
A
ypl zpl
R
I R
W
y R
W W
R R
W y dA y A R
W W
π
π
π
π
= = =
= =
= = = =
= =
∫

43
3.-Criterio de Von Mises de dimensionamiento:
Si aplicásemos el criterio de dimensionamiento de Von-Mises (sección 3.7), llegaríamos al
mismo resultado que con el criterio elástico de dimensionamiento.
En efecto, la fórmula de Von Mises es:
Caso del Momento Flector: Mz:
Caso del Momento Flector: My:
Observación: La Normativa indica las clases de secciones a las que aconseja aplicar el cálculo
elástico o el plástico.
*2 *2
3.co ydfσ σ τ= + ≤
* * *
* *max
max
*
*
.
siendo : 0 ysustituyendo
/
.
z z z
z z zel
z
co yd z zel yd
zel
M y M M
I I y W
M
f M W f
W
σ τ
σ
= = = =
= ≤ → ≤
* * *
max* *
max
*
*
.
siendo : 0 ysustituyendo
/
.
y y y
y y yel
y
co yd y yel yd
yel
M z M M
I I z W
M
f M W f
W
σ τ
σ
= = = =
= ≤ → ≤
* * ** * *
max* *max
max max
* * ** * *
, ,
..
siendo : 0
/ /
ysustituyendo
1 1
. .
y y yz z z
z y z y zel yel
y y yz z z
co yd
zel yel zel yd yel yd zel d yel d
M z M MM y M M
I I I y I z W W
M M MM M M
f
W W W f W f M M
σ τ
σ
= + = + = + =
= + ≤ → + ≤ → + ≤

44
5.5.2.-RESISTENCIA DE LAS SECCIONES A CORTADURA
Para el cálculo debido a las Fuerzas Cortantes, la normativa propone un cálculo plástico de las
mismas suponiendo unas distribuciones de tensiones cortantes uniformes.
1.-Criterio plástico de dimensionamiento:
El estudio se hará indistintamente para las cortaduras: Vy o Vz y la denominaremos en
general: V
A la fuerza cortante V que producen la tensión cortante del límite elástico τyd en todos puntos
de la sección, se le denomina: Vpl,d y representa la resistencia plástica de una sección a la
cortadura V. Calculemos su valor:
Según vimos en la sección 3.7, en el criterio de dimensionamiento de Von Mises, la tensión
cortante en el límite elástico tenía el siguiente valor :
Si suponemos, como dijimos antes, una distribución uniforme de las tensiones cortantes a lo
largo de la sección, tendremos:
Para obtener la resistencia plástica de la sección a esfuerzos cortantes, se procederá del
siguiente modo:
(verecuación 3.27)
3
yd
yd
f
τ =
Vpl,d
τ = τyd = fyd/√3 =
cte
Fig.5.48
, yd0 . (como cte) . (y por la ecuación 3.27)
.
3
v v
pl d ydA A
yd
v
F V dA dA
f
A
τ τ τ τ= → = = = = = = =
=
∑ ∫ ∫

45
Quedará pues:
• Secciones macizas de gran espesor: rectangulares, circulares,…….
Av = A (área de la sección)
• Perfiles abiertos de pequeño espesor: IPE, HEB, UPN,……….
Con cortadura Vy: Av = Área del alma del perfil
Con cortadura Vz: Av = Área de las alas del perfil
• Perfiles cerrados de pequeño espesor circulares:
Av = A.2/π
• Perfiles cerrados de pequeño espesor rectangulares:
Con cortadura Vy: Av = Área de las almas de los perfiles
Con cortadura Vz: Av = Área de las alas de los perfiles
Ejemplo:
, .
3
yd
pl d v
f
V A= (5.52)
,
siendo:
:"resistencia plástica de la sección a la cortadura V"
:"área de la sección a considerar, según el tipo de la misma":
pl d
v
V
A
h
b
tw
tf
d
Vy → Av ≈ h.tw
Vz → Av ≈ A-.d.tw

46
Así pues para comprobar la resistencia plástica de una sección a cortadura:
V*
(carga mayorada) = fuerza cortante que solicita a la sección, que se obtiene de los
diagramas de esfuerzos
2.-Criterio de Von Mises de dimensionamiento:
Si aplicásemos el criterio de dimensionamiento de Von-Mises (sección 3.7), sólo para las
Fuerzas Cortantes, llegaríamos al mismo resultado que con el criterio plástico de
dimensionamiento visto anteriormente.
En efecto, la fórmula de Von Mises es:
*
* *
*
*
: 0 (sup )
: 3. .
3
v
yd
yd v
v
V
siendo oniendodistribuciónuniforme
A
fV
y sustituyendo f V A
A
σ τ= = =
≤ → ≤
5.5.3.-RESISTENCIA DE LAS SECCIONES A FLEXIÓN SIMPLE: MOMENTOS
FLECTORES Y FUERZAS CORTANTES
Se estudiarán los dimensionamientos vistos para los Momentos Flectores y para las Fuerzas
Cortantes separadamente y si se cumple que:
Esto ocurrirá en la mayoría de los casos y en el caso de que no se cumpliese habría que hacer
una nueva comprobación combinando el Momento flector con la Fuerza Cortante (ver
Normativa DB-SE-A)
*
, .
3
yd
pl d v
f
V V A≤ =
*2 *2
3.co ydfσ σ τ= + ≤
(5.53)
*
,
1 1
. . . nohabrá quehacer mascomprobaciones
2 2 3
yd
pl d v
f
V V A≤ = →

47
5.5.4.-RESISTENCIA DE LAS BARRAS METÁLICAS A FLEXIÓN
Al considerar ahora la barra en su conjunto, se tendrán que hacer nuevas comprobaciones:
1.- Comprobación del Pandeo Lateral debido a la flexión: al tener la viga zonas comprimidas,
si éstas no presentan una rigidez suficiente, la viga, si no está suficientemente rigidizada
lateralmente, podrá flexar lateralmente al mismo tiempo que torsionarse. Esto puede ocurrir
en vigas metálicas.
2.-Comprobación de la rigidez del alma de una barra bajo cargas concentradas
3.-Abolladura del alma por cortante
Ëstas comprobaciones son objeto de estudio en otras asignaturas. (Ver la Normativa española
sobre Estructuras de acero en la edificación: DB-SE-A)
Para otros materiales existen las Normativas específicas: caso del Hormigón y madera
⇒
Fig.5.49.a
Fig.5.49.b

48
OBSERVACIONES:
Para efectuar el dimensionamiento completo de una viga que trabaje a Flexión habrá que
realizar, además del dimensionamiento a resistencia que se acaba de ver, la comprobación a
rigidez: limitación de la flecha máxima. (Se verá en el capítulo siguiente)
ymax
Fig.5.50

Flexión: Tensiones máximas

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Destacado

Destacado (20)

Similar a Flexión: Tensiones máximas

Similar a Flexión: Tensiones máximas (20)

Último

Último (20)

Flexión: Tensiones máximas