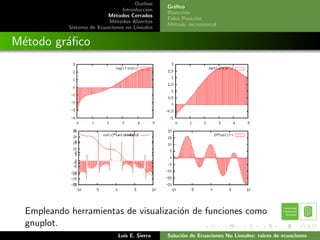
Este documento presenta diferentes métodos para resolver ecuaciones no lineales, incluyendo métodos cerrados como bisección, posición falsa e incremental, y métodos abiertos como iteración de punto fijo, Newton-Raphson y secante. Explica los algoritmos de cada método y provee ejemplos numéricos para ilustrarlos.

1. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
´ ´
Metodos Numericos
´
Solucion de Ecuaciones No Lineales:
raices de ecuaciones
Luis E. Sierra1
Universidad Industrial de Santander
Escuela Ingenier´ de Petr´leos
ıa o
Bucaramanga 16 Nov 2007
1
Ing. Petr´leos LuisE.Sierra@yahoo.co.uk
o
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

2. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
CONTENIDO
1 Introducci´n
o
2 M´todos Cerrados
e
Gr´fico
a
Bisecci´n
o
Falsa Posici´n
o
M´todo incremental
e
3 M´todos Abiertos
e
Iteraci´n de Punto Fijo
o
Newton-Raphson
Secante
Ra´ M´ltiples
ıces u
4 Sistema de Ecuaciones no Lineales
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

3. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Introducci´n
o
Determine la raiz de
f (x) = log (x) − sen(x)
f (x) = sen(x)tan(x) − |x|
√
f (x) = x − cos(x)
f (x) = 10 ∗ cos(x) − x
Lo puede hacer de forma expl´cita ?
ı
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

4. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
M´todos Cerrados
e
Aprovecha el cambio de signo de la funci´n en la vecindad de la
o
ra´
ız.
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

5. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
M´todo gr´fico
e a
Empleando herramientas de visualizaci´n de funciones como
o
gnuplot.
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

6. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
M´todo de bisecci´n
e o
Es un m´todo que se basa en el teorema del valor intermedio
e
Suponga que f (x) es una funci´n continua en [a, b] con f (a) y
o
f (b) de signos diferentes. Entonces existe un n´mero p en (a, b)
u
t.q. f (p) = 0
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

7. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
De forma iterativa lo que se hace es:
Calcular un valor medio en el intervalo [ai , bi ] designado por
ai + bi
pi = (1)
2
Si f (pi ) = 0 entonces p = pi , listo
De lo contrario evaluar los signos de f (pi ) y f (bi ) si son
opuestos entonces p ∈ [pi , bi ] y se hace ai+1 = pi y bi+1 = bi
y se calcula Pi+1
De no cumplirse el literal anterior entonces ai+1 = ai y
bi+1 = pi y calcular pi+1
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

8. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
Ejercicio
√
Determinar la raiz para f (x) = x − cos(x) en el intervalo [0, 1.5]
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

9. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
Ejercicio
√
Determinar la raiz para f (x) = x − cos(x) en el intervalo [0, 1.5]
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

10. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
Algoritmo
Entrada a, b, TOL, Numero iteraciones No
Paso 1: tome i=1, FA=f(a)
Paso 2: Mientras i<=No haga paso 3-6
Paso 3: Tome p=(a+b)/2; calcular p
FP=f(p)
Paso 4: Si FP=0 o (b-a)/2<TOL entonces
salida p Parar
Paso 5: Si FA*FP>0 entonces tome a=p;
(Calcular ai,bi)
FA=FP
Paso 6: Si no tomar b=p
Paso 7: Salida
Implementar en c++ empleando el editor gvim y el
compilador g++
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

11. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
M´todo de la Falsa Posici´n o Interpolaci´n lineal
e o o
Es un m´todo que a diferencia del m´todo de bisecci´n considera
e e o
las magnitudes de las funciones f (ai y f (bi ). para ubicar una falsa
posici´n de la raiz por medio de una l´
o ınea recta. De aqu´ su
ı
nombre.
f (b) f (a)
tan(θ) = b−p = − p−a
af (b)−bf (a)
p= f (b)−f (a)
f (b)(b − a)
p=b− (2)
f (b) − f (a)
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

12. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
Algoritmo
Entrada a, b, TOL, No
Paso 1: Tome i=2;
qa=f(a); qb=f(b);
PAso 2: Mientras i<=No haga paso 3-7
Paso 3: Tome p=b-qb(b-a)/(qb-qa). (Calcula pi)
Paso 4: Si |p-pi|<TOL entonces
Salida (p)(procedimiento termindo
exitosamente). Parar
Paso 5: Tome i=1+1
pi=p; qi=f(pi)
Paso 6: Si qi*qb<0 entonces tome a=p;
qa=qb;
Paso 7 Tome b=p;
qa=qi
Paso 8: SALIDA (El metodo supero las No iteraciones.
Termino sin exito) Ecuaciones No Lineales: raices de ecuaciones
Luis E. Sierra Soluci´n de
o

13. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
Falsa posici´n modificado
o
Determinar la raiz de f (x) = x 10 − 1 en el intervalo [0, 1.3]
empleando bisecci´n y falsa posici´n. Observar que ocurre.
o o
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

14. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
Falsa posici´n modificado
o
Determinar la raiz de f (x) = x 10 − 1 en el intervalo [0, 1.3]
empleando bisecci´n y falsa posici´n. Observar que ocurre.
o o
modidicaci´n
o
En este m´todo se divide a la mitad el valor de la funci´n en el
e o
punto del intervalo que se esta presentando estancamiento
Implementar esta condici´n en el c´digo de falsa
o o
posici´n y evaluar el ejercicio. Qu´ observa?
o e
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

15. Outline
Gr´fico
a
Introducci´n
o
Bisecci´n
o
M´todos Cerrados
e
Falsa Posici´n
o
M´todos Abiertos
e
M´todo incremental
e
Sistema de Ecuaciones no Lineales
M´todo de busqueda incremental
e
Realizar busquedas incrementales evaluando el signo de la funci´n
o
Si existen multiple raices, dependiendo de la longitud del
incremento las puede pasar por alto
La soluci´n parcial es evaluar f (a) y
o
f (b) para identificar la presencia de
m´ximos o m´
a ınimos en el intervalo.
Es necesario complementar con gr´ficas
a
y comprensi´n del problema f´
o ısico.
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

16. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
M´todos Abiertos
e
Son m´todos que parten de un valor o intervalo que no
e
necesariamente contiene la raiz.
Estos m´todos pueden converger o diverger.
e
Si el m´todo converge por lo general lo hace m´s r´pido que los
e a a
m´todos cerrados.
e
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

17. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
Iteraci´n de Punto Fijo
o
Punto fijo
Un punto fijo de una funci´n g es un n´mero k para el cual
o u
g(k)=k. Ej. g (x) = x 2 − 2; g(-1)=-1 y g(2)=2
Emcontrar ra´ y puntos fijos son equivalentes en el sentido que:
ıces
Para encontrar una ra´ f(p)=0, podemos definir una funci´n g
ız o
con punto fijo en p de diversas formas donde solo algunas
convergen. Si la funci´n g tiene punto fijo en p entonces la funci´n
o o
definida por f(x)=x-g(x) tiene cero en p.
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

18. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
se garantiza existencia y unicidad del punto fijo con el siguiente
teorema
Teorema de punto fijo
Sea g ∈ C [a, b] t.q g (x) ∈ [a, b] para toda x en [a,b]. Adem´s
a
suponer que existe g en (a,b) y una constante 0 < k < 1 t.q
g (x) ≤ k para toda x ∈ (a, b)
Entonces la sucesi´n definida por pn = g (pn−1 ) con n ≥ 1
o
converge al unico valor fijo p en [a,b]
´
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

19. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
Algoritmo
Entrada f(x),po, No
Paso 1 Tome i=1
Paso 2 Mientras i<=No haga paso 3-6
Paso 3 Definimos la funci’on g(x) (Despejando f(x)
convenientemente para que x=g(x) y g’(x)<1)
p=g(po)
Paso 4 Si |p-po| < TOL
Salida (p) Termina exitosamente
Paso 5 Tome i=1+1
Paso 6 po=p
Paso 7 Salida Supero las iteraciones No
Terminado sin exito
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

20. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
M´todo de Newton-Raphson
e
Si aproximamos la funci´n f(x) por la serie de Taylor
o
2
f (x) = f (˜) + f (˜)(x − x ) + f (ε)(˜) (x−˜)
x x ˜ x 2
x
2
f (p) = 0 = f (˜) + f (˜)(p − x ) + f (ε)(˜) (p−˜)
x x ˜ x 2
x
f (˜)
x
El termino (p − x )2 es bastante peque˜o entonces: p ≈ x −
˜ n ˜ f (˜)
x
f (pn−1 )
pn = pn−1 − (3)
f (pn−1 )
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

21. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
convergencia
El siguiente teorema de convergencia para el m´todo de Newton
e
muestra la importancia de la elecci´n de po
o
Teorema
Sea f ∈ C [a, b]. Si p ∈ [a, b] t.q. f(p)=0 y f (p) = 0 entonces
existe δ > 0 t.q. el m´todo de Newton genera una sucesi´n [pn ]∞
e o n=1
converge a p para cualquier aproximaci´n inicial p0 ∈ [p − δ, p + δ]
o
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

22. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
M´todo de la secante
e
Es una modificaci´n al m´todo de Newton para superar la
o e
condici´n que f (x) = 0. Para esto:
o
f (pn−1 ) − f (pn−2 )
f (pn−1 ) ≈
pn−1 − pn−2
Remplazando en el m´todo de Newton-Raphson obtenemos
e
f (pn−1 )(pn−1 − pn−2 )
pn = pn−1 − (4)
f (pn−1 ) − f (pn−2 )
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

23. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
Secante modificado
f (pn−1 + δpn−1 ) − f (pn−1 )
f (pn−1 ) ≈
δpn−1
Remplazando en la en el m´todo de Newton-Raphson obtenemos
e
δpn−1 f (pn−1 )
pn = pn−1 − (5)
f (pn−1 + δpn−1 ) − f (pn−1 )
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

24. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
Ra´ m´ltiples
ıces u
Teorema
La funci´n f ∈ C m [a, b] tiene un cero de multiplicidad m en p y
o
(a,b) si y s´lo si f (p) = f (p) = ... = f m−1 (p) = 0 pero fm (p) = 0
o
La funci´n tiene ra´ sencilla en p si f(p)=0 pero f (p) = 0
o ız
.
Si tiene multiples ra´ f(x) se puede escribir como
ıces
f (x) = (x − p)m q(x), donde el limx→p q(x) = 0
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

25. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
Ra´ m´ltiples pares no presentan cambio de signo
ıces u
Figure: exp(x)(x − 1)2
Figure: exp(x)(x − 1)3
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

26. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
El m´todo de Newton-Raphson en los puntos de raices multiples
e
disminuye su velocidad de converegencia de un orden cuadr´tico a
a
uno lineal Para mantener un orden cuadr´ico es necesario que:
a
f (pi−1 )
pi = pi−1 − m
f (pi−1 )
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

27. Outline
Iteraci´n de Punto Fijo
o
Introducci´n
o
Newton-Raphson
M´todos Cerrados
e
Secante
M´todos Abiertos
e
Ra´ıces M´ltiples
u
Sistema de Ecuaciones no Lineales
El m´todo de Newton-Raphson en los puntos de raices multiples
e
disminuye su velocidad de converegencia de un orden cuadr´tico a
a
uno lineal Para mantener un orden cuadr´ico es necesario que:
a
f (pi−1 )
pi = pi−1 − m
f (pi−1 )
.
otra opci´n es tomar u(x) = ff (x) entonces
o (x)
pi = pi−1 − u(pp−1 )/u (p − 1), donde las ra´ de u(x) son las
ıces
ra´ de f(x), remplanzando se obtiene:
ıces
f (pi−1 )f (pi−1 )
pi = pi−1 − (6)
[f (pi−1 )]2 − f (pi−1 )f (pi−1 )
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

28. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Sistema de Ecuaciones No Lineales
Un sistema de ecuaci´nes es no lineal si no se puede expresar cada
o
una de sus ecuaciones como
f (x) = a1 x1 + a2 x2 + a3 x3 + ... + an xn
f1 (x1 , x2 , x3 , ..., xn = 0
f2 (x1 , x2 , x3 , ..., xn = 0
.
fn (x1 , x2 , x3 , ..., xn = 0
.
Haciendo la expanci´n por series de Taylor:
o
n
∂fi
fi (x + ∆x) = fi (x) + ∆xj + O(∆x 2 )
∂xj
j=1
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

29. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Truncando la serie y colocando de forma matricial
f(x + ∆x) = f(x) + J(x)∆x = 0
∂fi
donde J(x) es la matriz jacobiana Jij = ∂xj
∂fi fi (x + ej h) − fi (x)
≈
∂xj h
∆x = ej h
h es un peque˜o incremento
n
ej vector unitario en la direcci´n xj
o
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

30. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Pasos para el m´todo de Newton
e
1 Estimat un vector soluci´n x
o
2 Evaluar f(x)
3 Computar la matriz jacobiana J(x)
4 Plantear el sistema de ecuaciones y solucionar para ∆X
5 Calcular el nuevo vector x y repetir el paso 2-5 hasta alcanzar
el criterio de parada
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

31. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Ejemplo
Determine el punto de intersecci´n entre el circulo x 2 + y 2 = 3 y la
o
hip´rbola xy=1
e
f1 (x, y ) = x 2 + y 2 − 3 = 0
f2 (x, y ) = xy − 1 = 0
∂f1 /∂x ∂f2 /∂y 2x 2y
J(x, y ) = =
∂f2 /∂x ∂f2 /∂y y x
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

32. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
El sistema de ecuaciones lineales J(x)∆x = −f(x) relacionadas con
el m´todo de Newton-Raphson es:.
e
2x 2y ∆x −x 2 − y 2 + 3
=
y x ∆y −xy + 1
Tomando el vector de valores iniciales
estimado de x = [x0 y0 ] = [0.5 1.5]
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

33. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
1ra itiraci´n: Sustituimos x0 = 0.5, y0 = 1.5 en la ecuaci´n
o o
anterior
1.0 3.0 ∆x 0.50
=
1.5 0.5 ∆y 0.25
Solucionamos el sistema para obtener ∆x1 = ∆y1 = 0.125
Entonces
x1 = 0.5 + 0.125 = y y1 = 1.5 + 0.125 = 1.625
2da iteraci´n: Los valores de x1 y y1 son sustituidos en el sistema
o
1.250 3.250 ∆x −0.031250
=
1.625 0.625 ∆y −0.015625
Entonces ∆x2 = ∆y2 = −0.00694 y
x2 = x1 + ∆x2 = 0.625 − 0.00694 = 0.61806
y2 = y1 + ∆y2 = 1.625 − 0.00694 = 1.61806
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

34. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Bibliograf´
ıa
BURDEN Richard L. & FAIRES Douglas J.
An´lisis Num´rico. 7ed Thomson Learning M´xico 2002
a e e
CHAPRA Steven C. & CANALE Raymound P.
M´todos Numericos para ingenieros. 4ed. McGrawHill M´xico 2002
e e
.
Beamer LaTeX
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o

35. Outline
Introducci´n
o
M´todos Cerrados
e
M´todos Abiertos
e
Sistema de Ecuaciones no Lineales
Nunca consideres el estudio como una obligaci´n, sino como
o
una oportunidad para penetrar en el bello y maravilloso
mundo del saber
Albert Einstein
Luis E. Sierra Soluci´n de Ecuaciones No Lineales: raices de ecuaciones
o