Capiii

Simulación Numérica de
Yacimientos
CAPÍTULO III: Técnicas Numéricas

Elkin Rodolfo Santafé Rangel
Ingeniero de Petróleos

Bucaramanga – Colombia © 2008

La aproximación por diferencias finitas

• Es ampliamente usada.
• Busca aproximar el concepto de derivada.
• Es una aproximación discreta.
• Para ser aplicada requiere generalmente de
un sistema de enmallado ortogonal.
• Aproxima la solución sobre un dominio físico
del tamaño de la celda que contiene al nodo
de interés.

© Elkin Santafé ● 2008 ● Simulación Numérica de Yacimientos
Santafé Simulació Numé CAP. III: Técnicas Numéricas
Numé

Serie de Taylor
f '' ( xi ) 2 f ''' ( xi ) 3 f n ( xi ) n
f ( xi +1 ) = f ( xi ) + f ' ( xi )h + h + h + ... + h + Rn
2! 3! n!

f (n +1) (ξ ) n +1
Rn = h
(n + 1)!

Numé

Tipos de Diferencia Finita
SERIE DE TAYLOR HACIA ADELANTE

f '' ( xi ) 2 f ''' ( xi ) 3 f n ( xi ) n
f ( xi +1 ) = f ( xi ) + f ' ( xi )h + h + h + ... + h + Rn
2! 3! n!
SERIE DE TAYLOR HACIA ATRÁS

f '' ( xi ) 2 f ''' ( xi ) 3 f n ( xi ) n
f ( xi −1 ) = f ( xi ) − f ' ( xi )h + h − h + ... + h + Rn
2! 3! n!

f ( xi +1 ) − f ( xi ) f ( xi ) − f ( xi −1 )
≈ f ' ( xi ) ≈ f ' ( xi )
h h
D.F. Progresiva D.F. Regresiva

Numé


SERIE DE TAYLOR HACIA ADELANTE

+
SERIE DE TAYLOR HACIA ATRÁS

2 f ''' ( xi ) 3
f ( xi +1 ) = f ( xi −1 ) + 2 f ' ( xi )h + h + ...
3!

f ( xi +1 ) − f ( xi −1 ) f ''' ( xi ) 2
f ' ( xi ) = − h − ...
2h 3!
D.F. Central

Numé


DEFINICIÓN GEOMÉTRICA

Numé

Orden de Truncamiento

f ( xi +1 ) − f ( xi ) f ( xi +1 ) − f ( xi )
≈ f ' ( xi ) + O(h ) = f ' ( xi )
h h

f ( xi ) − f ( xi −1 ) f ( xi ) − f ( xi −1 )
≈ f ' ( xi ) + O(h ) = f ' ( xi )
h h

f ( xi +1 ) − f ( xi −1 ) f ( xi +1 ) − f ( xi −1 )
f ( xi ) ≈
'

2h
f ( xi ) =
'

2h
+ O h2 ( )

Numé

EDP´s

∇ U =0 2
ELÍPTICA
• Laplace

∇ U = f (x)
2 • Poisson

∂U
∇U= 2
PARABÓLICA
∂t
1∂U 2
∇U= 2
HIPERBÓLICA (Onda)
C ∂t 2

Numé

Esquemas de aproximación en 1D

EXPLÍCITA – Molécula Computacional 1D

ti +1
dimensión temporal

Δt

ti
xi −1 Δx xi xi +1

dimensión espacial

Numé


IMPLÍCITA – Molécula Computacional 1D
xi −1 xi xi +1
dimensión temporal

ti +1
Δx

Δt

ti

dimensión espacial

Numé


CASO TIPO: Modelo difusivo en 1D

Aproximando numéricamente:

∂ 2 P Pi +1 − 2 Pi + Pi −1 Varían los índices asociados
≈
∂x 2
Δx 2 al espacio.

∂P P n +1 − P n Varían los índices asociados
≈ al tiempo.
∂t Δt
Índice de tiempo
Esto genera una doble notación:
P Índice de espacio

Numé


CASO TIPO: Modelo difusivo en 1D

Los índices dependerán del esquema:

⎛ Pi +1 − 2 Pi n + Pi −1 ⎞ Pi n +1 − Pi n
n n
⎛ Pi +1 1 − 2 Pi n +1 + Pi −1 1 ⎞ Pi n +1 − Pi n
n+ n+

⎜ ⎟= ⎜ ⎟=
⎝ Δx 2
⎠ Δt ⎝ Δx 2
⎠ Δt
Explícito Implícito simple

Δt Δt
Δx 2
( Pi+1 − 2Pi + Pi−1 ) = Pi − Pi Δx 2 ( Pi+n1+1 − 2Pi n+1 + Pi−n1+1 ) = Pi n+1 − Pi n
n n n n +1 n

λ ( Pi +1 − 2 Pi n + Pi −1 ) = Pi n +1 − Pi n
n n
λ ( Pi +1 1 − 2 Pi n +1 + Pi −1 1 ) = Pi n +1 − Pi n
n+ n+

Numé


CASO TIPO: Ecuación de conducción de calor en 1D

Los índices dependerán del esquema:

Explícito Implícito simple

λ ( Pi +1 − 2 Pi n + Pi −1 ) = Pi n +1 − Pi n
n n
λ ( Pi +1 1 − 2 Pi n +1 + Pi −1 1 ) = Pi n +1 − Pi n
n+ n+

? Pi n +1 1 incógnita
1 ecuación ? Pi +1 1 , Pi n +1 , Pi −1 1
n+ n+ 3 incógnitas
1 ecuación

Pi n +1
= Pi + λ ( P − 2 Pi + P
n n
i +1
n n
i −1 ) −λ Pi +1 1 + (1 + 2λ ) Pi n +1 − λ Pi −1 1 = Pi n
n+ n+

Solución directa ! Sistema de ecuaciones !

Numé

CASO TIPO: Modelo Difusivo en 1D

Aproximación de CRANK - NICHOLSON: esquema implícito alternativo, con
exactitud de segundo orden para el espacio y el tiempo.

Implícito simple Crank - Nicholson

xi −1 xi xi +1 xi −1 xi xi +1
ti +1

ti + 1 2
Punto intermedio
ti
Comparación entre las moléculas computacionales asociadas a cada esquema
Numé

CASO TIPO: Ecuación de conducción de calor en 1D

Implícito simple Crank - Nicholson

⎛ Pi +1 − 2 Pi n + Pi −1
n n
⎞
∂ 2 P Pi +1 1 − 2 Pi n +1 + Pi −1 1
n+ n+
⎜ + ⎟
≈ ∂ P 1
2
Δx 2

∂x 2
Δx 2 ≈ ⎜ n +1 ⎟
∂x 2
2 ⎜ Pi +1 − 2 Pi + Pi −1 ⎟
n +1 n +1

► Toda la aproximación espacial se ⎜ ⎟
hace en n+1 ⎝ Δx 2 ⎠
► Se toma por referencia el punto
intermedio y se promedia la variación
∂P P n +1 − P n espacial en n+1 y en n.
≈
∂t Δt n +1 ► Se construye con
∂P P − P n
una D.F. Central
► Diferencia finita progresiva con ≈ alrededor del punto
aproximación de primer orden. ∂t Δt intermedio.

Numé

Sistemas de ordenamiento en 1D
1 2 3 4 5 6 7 8

► Forma general de la matriz.
Esta refleja las relaciones existentes
entre las celdas que componen la
malla.
La matriz resultante para este caso
es una tridiagonal.

Numé

Métodos de Solución

Método de Thomas

Método de Ciclo reducción

Numé

Problema de Frontera

Punto
Centrado

Punto
Distribuido

Numé


Condiciones de primera clase
Se conoce también con el nombre de condiciones tipo
Dirichlet.

U ( izq, t ) = f1 ( t )
U ( der , t ) = f 2 ( t )

u n
izq = f1 ( t n
) n = 0,1,...

Numé


Condiciones de primera clase

uizq = f1 X
u1 + u0
f1 =
Tiene implicaciones a 2
nivel de la forma como
se expresa la condición
de frontera. 0 1

uizq = f1

Numé


Condiciones de segunda clase
Se conoce también con el nombre de condiciones tipo
Neumann.

∂U
= f1 ( t )
∂x
1 2

X 1 2

∂u ∂u
= f1 = f1
∂x ∂x
Numé


Condiciones de segunda clase

f1 ( t
(u n
−u n
)
n
) ≈
2

Δx
1

u − u0 n n
u − u0 n n
f = n 1
f = n 1

Δx Δx
1 1

0

-1 0 1

Numé


Condiciones de tercera clase
Se obtiene por una combinación de las dos condiciones
anteriores.

∂U
a + bU = f1 ( t )
∂x
II
I

U II u1 u2
0
Numé


Considere que el reservorio I se encuentra conectado en
X=0 con otro yacimiento de presión promedio conocida. Se
requiere incluir la influencia del segundo yacimiento a
través de la condición límite en X=0. El flujo desde el
yacimiento II al I viene dado por:

qII → I ( t ) = b ⎡U II ( t ) − u1 ⎤
⎣ ⎦
donde b es una constante de proporcionalidad similar al
índice de productividad.

Numé


De otro dentro del yacimiento I, la tasa de flujo debe
satisfacer la Ley Darcy:

∂U
qII → I ( t ) = a
∂x
Estas dos ecuaciones combinadas da la ecuación de
condición límite combinada dada a continuación:

∂U
a + bU = bU II ( t )
∂x
Numé


Para una malla de punto distribuido se tendrá la siguiente
aproximación:

a ⎡u − U ⎤
⎣
n
⎦ + bu n = bU n
2
n
II

2Δx
1 II

Numé

Esquemas de Aproximación en 2D

Ecuaciones Elípticas

∂2P ∂2 P
+ 2 =0 Ecuación de Laplace
∂x 2
∂y

∂ P ∂ P
2 2
+ 2 = f ( x, y ) Ecuación de Poisson
∂x 2
∂y

Fuentes o pérdidas
de calor.

Numé

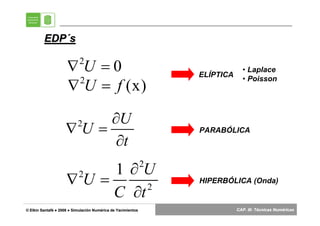
CASO TIPO: Ecuación de Laplace

∂ 2 P Pi +1 − 2 Pi + Pi −1 ∂ 2 P Pj +1 − 2 Pj + Pj −1
≈ ≈
∂x 2
Δx 2 ∂y 2
Δy 2

Pi +1, j − 2 Pi , j + Pi −1, j Pi , j +1 − 2 Pi , j + Pi , j −1
+ =0
Δx 2
Δy 2

[
O Δ(x )
2
] [
O Δ( y )
2
]
Numé


Ecuaciones Parabólicas

∂ 2 P ∂ 2 P ∂P
+ 2 =
∂x 2
∂y ∂t

Esquema Explícito
1
8
(
Δt ≤ ( Δx ) + ( Δy )
2 2
)
Dejan de ser tridiagonales y
Esquema Implícito se pueden convertir en
matrices dispersas.

Numé

Sistemas de ordenamiento

► En 2D, la forma de la geometría
se determina con el sentido del
ordenamiento. Si se escoge un
ordenamiento normal, el resultado
será una matriz con 5 diagonales y
un somero grado de dispersión.

Numé

Numé

Métodos de solución

Método de Jacobi
Método de Gauss - Seidel
Método SOR
Método PSOR
Método LSOR
Método LSORC
Esquema IDA

Numé

Concepto de Stencil
i
El concepto de Stencil permite
expresar los modelos de forma
generalizada.
Wi Ci Ei
TCi , j ,k
Ni , j Ei , j Ni , j ,k
Wi , j ,k Ei , j ,k
i, j
Si , j , k
Wi , j Si , j
BCi , j ,k
Numé

Concepto de Stencil

i-1 i i+1

► Modelo de Stencil para
Wi Ci Ei un sistema unidimensional.

−λ Pi −1 1 + (1 + 2λ ) Pi n +1 − λ Pi +1 1 = Pi n
n+ n+

n +1 n +1 n +1
WP i i −1 + Ci Pi +EP
i i +1 = Fi

Numé

Concepto de Stencil

► Distribución de Stencils para un sistema unidimensional.

Numé

Concepto de Stencil

Ni , j
Pi +1, j + Pi −1, j − 4 Pi , j + Pi , j +1 + Pi , j −1 = 0
Ei , j
Ei , j Pi +1, j + Wi , j Pi −1, j + Ci , j Pi , j +
i, j
Wi , j N i , j Pi , j +1 + Si , j Pi , j −1 = Fi , j

► Modelo de Stencil para
Si , j un sistema bidimensional.

Numé

Concepto de Stencil

• En la frontera se debe ajustar de acuerdo a la ecuación
que rija el fenómeno allí.

• Algunos stencils pueden anularse y otros tomar valores
que carecen de sentido físico.

• Dependiendo de las características del sistema se pueden
dar condiciones de simetría.

Numé

Condición del Sistema
Error de Truncamiento

► Definición para un
esquema explícito

Numé

Error de Truncamiento

Hacen que el error tienda a cero
cuando ellos tienden a cero.
Se puede afirmar que el esquema
es consistente.

Numé

Estabilidad

Numé

Estabilidad

Existen dos criterios muy utilizados para desarrollar el
análisis de estabilidad de un sistema:

• Criterio de Karplus: no tiene en cuenta el efecto de las
condiciones de borde en el límite.

• Análisis Armónico: se basa en series de Fourier.

Numé

Estabilidad

Criterio de Karplus:
La ecuación en diferencias finitas es reordenada de tal
manera que adquiera la siguiente forma:

Cambio en Cambio en Término de
subíndices superíndices referencia

Numé

Estabilidad

• Si todos los coeficientes son negativos el esquema es
estable.

• Si solo algunos de los coeficientes son negativos,
entonces la suma de os mismos debe ser menor o igual
que 0.

Numé

Estabilidad


Corroborar para un esquema implícito

Numé

Estabilidad

Análisis Armónico:
Se debe aplicar la definición general al esquema numérico:

La ecuación toma una forma dependiendo del esquema.

Numé

Estabilidad


► Formulación para un esquema
implícito

Numé

Estabilidad


► Formulación para un esquema
explícito.

Numé

Estabilidad


Numé

Estabilidad


Se toma el n-ésimo
término.

Se debe analizar el
cambio del error en el
tiempo.

Numé

Estabilidad


Factor de Condición de
amplificación. estabilidad.

Numé

P-SOR

P ( k +1)
i, j = (1 − w ) P + wP
k
i, j
*( k +1)
i, j

1
P *( k +1)
= ⎡ Fi , j − Wi. j Pi −1,1j − Si. j Pi ,kj+−11 − N i , j Pi ,kj +1 − Ei , j Pi +1, j ⎤
k+ k

Ci , j ⎣ ⎦
i, j

Numé

L-SOR

Estos valores se
determinan
simultáneamente

Numé

L-SOR
⎛ ⎡ Fi , j − Wi. j Pi −1,1j
k+
⎤⎞
⎜ 1 ⎢ ⎥⎟
P ( k +1)
i, j = (1 − w ) Pi , j + w ⎜
k k +1
⎢ − Si. j Pi , j −1 − N i , j Pi , j +1 ⎥ ⎟
k

⎜ Ci , j ⎢ ⎥⎟
⎜ ⎢ − Ei , j Pi +1, j
k
⎥⎟
⎝ ⎣ ⎦⎠

Fi , j Wi , j Si , j
P ( k +1)
i, j = (1 − w ) P + w k
i, j −w P k +1
i −1, j −w P k +1
i , j −1
Ci , j Ci , j Ci , j
Ni, j Ei , j
−w P k
i , j +1 −w P k
i +1, j
Ci , j Ci , j
Numé

L-SOR
Se hace necesario ajustar este superíndice
a la iteración correspondiente

Wi , j Ei , j Fi , j
w P k +1
i −1, j +P ( k +1)
i, j +w P k
i +1, j = (1 − w ) P + w
k
i, j
Si , j k +1
Ni, j
−w P i , j −1 −w P k
i , j +1
Ci , j Ci , j

Numé

L-SOR

Wi , j Ei , j Fi , j
w P k +1
i −1, j +P ( k +1)
i, j +w P k +1
i +1, j = (1 − w ) P + w
k
i, j
Si , j k +1
Ni, j Esto genera como resultado un
−w P i , j −1 −w P k
i , j +1 sistema tridiagonal por fila
Ci , j Ci , j recorrida…

Se aplica el siguiente criterio
de convergencia:

Numé

L-SORC o WATTS SOR

Lo que se busca con este método es repartir el error residual
producto de la aproximación

Numé

L-SORC o WATTS SOR

Wi. j Pi −1, j + Si. j Pi ,kj −1 + Ci , j Pi ,kj + N i , j Pi ,kj +1 + Ei , j Pi +1, j − Fi , j = ri kj
k k
,

Numé

L-SORC o WATTS SOR

Wi. j ( Pi −1, j − Pi *1 ) + Si. j ( Pi ,kj −1 − Pi * ) + Ci , j ( Pi ,kj − Pi * )
k
−

+ N i , j ( Pi ,kj +1 − Pi * ) + Ei , j ( Pi +1, j − Pi*1 ) − Fi , j = 0
k
+

Si se escribe la ecuación inicial para cada uno de los bloques de la
columna i y luego se suman todas las ecuaciones se obtiene:

J J J J

∑Wj =1
P k
i . j i −1, j +∑S P
j =1
k
i . j i , j −1 + ∑C P + ∑ N P
j =1
k
i, j i, j
j =1
k
i , j i , j +1

J J J
+ ∑ Ei , j Pi +1, j − ∑ Fi , j = ∑ ri kj
k
,
j =1 j =1 j =1

Numé

L-SORC o WATTS SOR

J J J J

∑ Wi. j Pi −1, j + ∑ Wi. j Pi *1 + ∑ Si. j Pi ,kj −1 + ∑ Si. j Pi *
j =1
k
−
j =1 j =1 j =1
J J J J
+ ∑ Ci , j Pi ,kj + ∑ Ci , j Pi * + ∑ N i , j Pi ,kj +1 + ∑ N i , j Pi *
j =1 j =1 j =1 j =1
J J J
+∑ E P k
i , j i +1, j + ∑ E P − ∑ Fi , j = 0 *
i , j i +1
j =1 j =1 j =1

Numé

L-SORC o WATTS SOR

J J J J

∑ −
Wi. j Pi *1 + ∑ Si. j Pi * + ∑ Ci , j Pi * + ∑ N i , j Pi *
j =1 j =1 j =1 j =1
J J
+ ∑ Ei , j Pi *1 = −∑ ri kj
+ ,
j =1 j =1

Numé

L-SORC o WATTS SOR

⎛ J ⎞ * ⎛ J J J ⎞ *
⎜ ∑ Wi. j ⎟ Pi −1 + ⎜ ∑ Si. j + ∑ Ci , j + ∑ N i , j ⎟ Pi
⎝ j =1 ⎠ ⎝ j =1 j =1 j =1 ⎠
⎛ J ⎞ * J
+ ⎜ ∑ Ei , j ⎟ Pi +1 = −∑ ri , j
k

⎝ j =1 ⎠ j =1

Numé

L-SORC o WATTS SOR

• Se aplica el método LSOR.
• Se calcula Pi * resolviendo el sistema tridiagonal.
• Se obtienen los valores corregidos.
• Se evalúa el criterio de convergencia.

Numé

Bibliografía

[1] SIERRA, Luis E. y SANTAFE, Elkin R. Simulación Numérica de Yacimientos.
Curso Pregrado II Semestre 2006. Universidad Industrial de Santander.
Bucaramanga-Colombia.

[2] SEPÚLVEDA, Jairo A. Simulación Numérica de Yacimientos. Apuntes de
Curso Pregrado. Universidad Surcolombiana. Marzo de 2002. Colombia.

[3] OSORIO, Gildardo. Notas de simulación numérica de yacimientos. Universidad
Nacional (Sede Medellín).

[4] AZIZ, Khalid y SETTARI, Antonín. Petroleum reservoir simulation. Elsevier
Appliedd Science Publishers. Londres y New York, 1979.

[5] H.B. Crichlow. Modern reservoir engineering – a simulation APPROACH.
Prentice Hall, 1977.

Numé

Atribución No Comercial 2.5 Colombia

Usted es libre de:

• Copiar, distribuir, exhibir y ejecutar la obra.
• Hacer obras derivadas.

Bajo las siguientes condiciones:

Atribución. Usted debe atribuir la obra en la
forma especificada por el autor o licenciante.

No comercial. Usted no puede usar esta obra
con fines comerciales.

Sus usos legítimos u otros derechos no son afectados de ninguna
manera por lo dispuesto precedentemente.

Este es un resumen legible-por-humanos del Código Legal (Licencia Completa).

http://creativecommons.org/licenses/by-nc/2.5/co/legalcode

Capiii

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Capiii

Más de fabianchopinto

Capiii