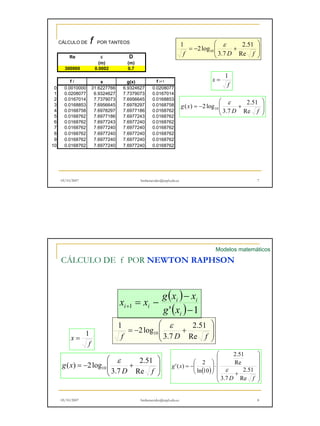
Este documento presenta métodos numéricos para calcular el coeficiente de fricción en redes de tuberías, incluyendo el método de punto fijo y el método de Newton-Raphson. Explica la ecuación de Colebrook-White para calcular f de forma implícita y provee ejemplos numéricos para ambos métodos. Finalmente, pide practicar cálculos manuales y computarizados de f usando estos métodos.

1. utpl ucg centro de investigaciones en ingeniería hidráulica & saneamiento
www.utpl.edu.ec
Hidráulica de tuberías
Redes ramificadas
Métodos numéricos
aplicados al cálculo del
coeficiente de fricción
Holger Benavides Muñoz
1. Diseño de redes ramificadas o
abiertas
1.2 Modelos matemáticos para redes
ramificadas.
‰ Conferencia 03:
“Métodos numéricos aplicados al cálculo del
coeficiente de fricción”
‰ Contenidos:
„ Punto fijo.
„ Newton - Raphson
Raphson.
„ Ejercicios de aplicación.
„ Apoyo ofimático al cálculo (Excel – solver).
05/10/2007 hmbenavides@utpl.edu.ec 2

2. Bibliografía
„ SALDARRIAGA, J. 2000. Hidráulica de tuberías.
Bogotá, Col., McGraw – Hill. 592 p.
„ SOTELO, G. 1987. Hidráulica General, vol. I,
fundamentos. México, Limusa. 561 p.
„ MATAIX, C. 1982. Mecánica de fluidos y máquinas
hidráulicas. 2ª de. México, HARLA.660 P.
„ PEREZ, R. 1993. Dimensionado óptimo de redes de
distribución de agua ramificadas. Universidad
Politécnica de Valencia. Tesis doctoral.
‰ Reconocimiento y agradecimiento: Dr. Ing. Rafael Pérez García. GMMF.
05/10/2007 hmbenavides@utpl.edu.ec 3
Modelos matemáticos
Darcy - Weisbach
„ La expresión para el cálculo de pérdidas en
sistemas de tuberías a presión es:

=  
2 8
2
h f L f  
f = factor de fricción
2
f L
2 5
Q
g D
g
V
D

 

  
=
π
L = longitud de tubería
D = diámetro interno
Q = caudal
05/10/2007 hmbenavides@utpl.edu.ec 4

3. Modelos matemáticos
Cálculo del factor de fricción.
„ Para tubos lisos o rugosos en la zona de transición
o turbulenta (para Re > 4000), se utiliza la ecuación
de Colebrook Colebrook-White para determinar el factor de
fricción f de forma implícita de la ecuación de
Darcy-Weisbach.
„ Mediante un sencillo cálculo iterativo de punto fijo o
por el método de Newton - Raphson, cuya
convergencia está asegurada para los valores de
Re y habitualmente empleados p
en redes de
distribución.

 

 
2.51
1 2log
ε
= − +
f 10
3.7
D Re f
05/10/2007 hmbenavides@utpl.edu.ec 5
Velocidad en función de pérdidas

 


 

v L
⋅ ⋅
2.51
⋅ ⋅ ⋅
⋅ +

 

 − ⋅ ⋅ ⋅
=
 

f
f
D g D h
g D h
L D
V
2
3.7
log
2 2
10
ε
05/10/2007 hmbenavides@utpl.edu.ec 6

4. CÁLCULO DE f POR TANTEOS ε
1

 

 
2.51
= − +
f 3.7
D Re f
1 2log
10
Re ε D
(m) (m)
300000 0.0002 0.7
f
x = 
 

 
= − +
2.51
D f
g x
Re
3.7
( ) 2 log10
ε
f i x g(x) f i+1
0 0.0010000 31.6227766 6.9324627 0.0208077
1 0.0208077 6.9324627 7.7379073 0.0167014
2 0.0167014 7.7379073 7.6956645 0.0168853
3 0.0168853 7.6956645 7.6978297 0.0168758
4 0.0168758 7.6978297 7.6977186 0.0168762
5 0.0168762 7.6977186 7.6977243 0.0168762
6 0.0168762 7.6977243 7.6977240 0.0168762
7 0.0168762 7.6977240 7.6977240 0.0168762
8 0.0168762 7.6977240 7.6977240 0.0168762
9 0.0168762 7.6977240 7.6977240 0.0168762
10 0.0168762 7.6977240 7.6977240 0.0168762
05/10/2007 hmbenavides@utpl.edu.ec 7
Modelos matemáticos
CÁLCULO DE f POR NEWTON RAPHSON
( )


x x g x x
i i
1 '( )−1
i i g x

2.51
x 1 =  
f

 
= − +
f 3.7
D Re f
1 2log
10
ε
−
= − +
i


'( )  2 ( )
ε    

   

2.51
Re
+

⋅  

= −
 
2.51
D f
g x
Re
3.7
ln 10

 
( ) 2log10
ε
= − +
2.51
D f
g x
Re
3.7
05/10/2007 hmbenavides@utpl.edu.ec 8

5. CÁLCULO DE f POR NEWTON RAPHSON
Re ε D
(m) (m)
308405 0.000001522 0.1522
Modelos matemáticos
f i x g(x) g'(x) Xi+1 f i+1
0 0.00100000 31.62277660 7.16982156 -0.02718175 7.81690675 0.01636553
1 0.01636553 7.81690675 8.35668789 -0.10658855 8.30469522 0.01449949
2 0.01449949 8.30469522 8.30619189 -0.10056864 8.30605513 0.01449474
3 0.01449474 8.30605513 8.30605514 -0.10055280 8.30605514 0.01449474
4 0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
5 0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
6 0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
7 0 01449474 8 30605514 8 30605514 0 10055280 8 30605514 0 01449474
0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
8 0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
9 0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
10 0.01449474 8.30605514 8.30605514 -0.10055280 8.30605514 0.01449474
05/10/2007 hmbenavides@utpl.edu.ec 9
Ejemplo de cálculo
Modelos matemáticos
„ Calcular el Q de agua que puede ser movido a través de
una tubería de PVC de 293 mm de diámetro. Longitud: 730
m, y con una carga gravitacional de: 43.5 m. Se asume
, g g
que la rugosidad absoluta (ε) en m es: 0.0000015. Por
coefc. global de pérdidas menores se espera un Kfm: 11.8.
La densidad del agua: 998.2 kg/m³. Viscosidad dinámica
(μ): 0.001005 Kg/(m.s).
„ Viscosidad cinemática ( ν): ) 0 0.001005 001005 / 998 998.2 2
=
Viscocidad cinemática: 1.00681E-06 m2/s
05/10/2007 hmbenavides@utpl.edu.ec 10

6. Modelos matemáticos

 


 

v L
⋅ ⋅
2.51
⋅ ⋅ ⋅
⋅ +

 

 − ⋅ ⋅ ⋅
=
 

f
f
D g D h
g D h
L D
V
2
3.7
log
2 2
10
ε

V 2

 
 
h H K f i fm 2
= − + 1
g
Q = 0.31250 m3/s
05/10/2007 hmbenavides@utpl.edu.ec 11
Deber
„ Practicar cálculos (a mano y en
computadora) para el cálculo de f
(Colebrook – White)
‰ Al menos 2 ejc. por los métodos de punto fijo
‰ Al menos 2 ejc. por el método de N-R.
05/10/2007 hmbenavides@utpl.edu.ec 12