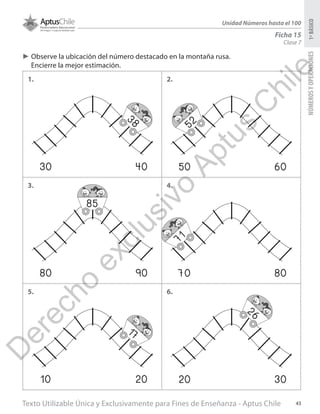
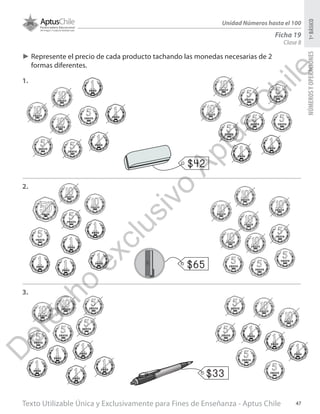
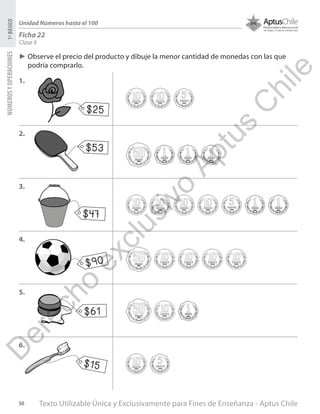
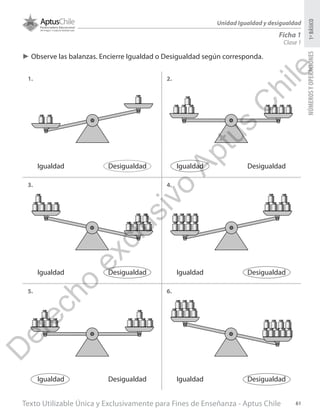
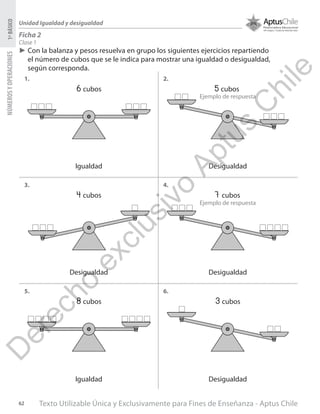
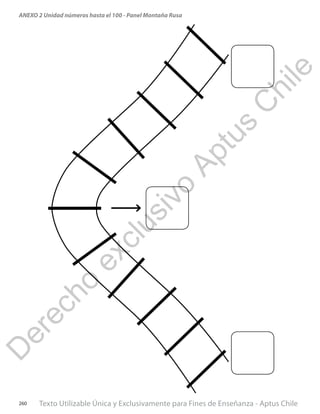
Este documento presenta una planificación para una unidad sobre números hasta 100 en matemáticas para primero básico. Incluye tres clases con objetivos de aprendizaje, materiales, actividades y ejercicios. La primera clase enseña a formar números con decenas y unidades hasta 99 usando bloques. La segunda clase cubre componer y descomponer números hasta 99. La tercera clase trata de representar números en forma estándar, desarrollada y con palabras. El documento provee información detallada para que el profesor enseñe estos concept