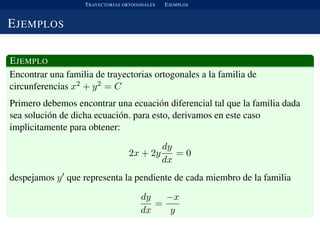
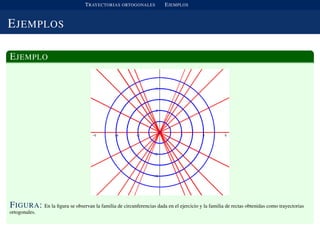
Este documento define trayectorias ortogonales como curvas que son perpendiculares a cada miembro de una familia de curvas. Explica que si una familia de trayectorias satisface una ecuación diferencial, entonces la familia ortogonal debe satisfacer la ecuación diferencial inversa. Proporciona como ejemplo que las elipses son ortogonales a las parábolas y que las rectas son ortogonales a las circunferencias.

2. TRAYECTORIAS ORTOGONALES
Diego Sandoval
Departamento de Matem´aticas, f´ısica y Estad´ıstica
Universidad de La Sabana

3. TRAYECTORIAS ORTOGONALES DEFINICI ´ON
TRAYECTORIAS ORTOGONALES
DEFINICI ´ON
Una curva que es ortogonal a cada miembro de una familia de curvas es
llamada una trayectoria ortogonal a la familia.
EJEMPLO
La familia de parabolas y = C1x2 es ortogonal a la familia de elipses
x2 + 2y2 = C2.
FIGURA: En la figura de la izquierda se observan la familia de parabolas y = C1x2
(familia1) y la familia de elipses
x2
+ 2y2
= C2 (familia 2). A la derecha se detalla un punto de cruce entre dos elementos de cada familia.

4. TRAYECTORIAS ORTOGONALES DEFINICI ´ON
TRAYECTORIAS ORTOGONALES
Si la familia de trayectorias dada, satisface la ecuaci´on diferencial
dy
dx
= f(x, y)
entonces, la familia de trayectorias ortogonales a esta debe satisfacer la
ecuaci´on diferencial
dy
dx
= −
1
f(x, y)
ya que cada una de estas ecuaciones describe la pendiente de cada elemento
de la familia en alg´un punto. y las curvas ser´an ortogonales ya que el producto
de las pendientes es −1.

5. TRAYECTORIAS ORTOGONALES EJEMPLOS
EJEMPLOS
EJEMPLO
Encontrar una familia de trayectorias ortogonales a la familia de
circunferencias x2 + y2 = C
Primero debemos encontrar una ecuaci´on diferencial tal que la familia dada
sea soluci´on de dicha ecuaci´on. para esto, derivamos en este caso
implicitamente para obtener:
2x + 2y
dy
dx
= 0
despejamos y que representa la pendiente de cada miembro de la familia
dy
dx
=
−x
y

6. TRAYECTORIAS ORTOGONALES EJEMPLOS
EJEMPLOS
EJEMPLO
Entonces, las trayectorias ortogonales deben satisfacer dy/dx = −1/f(x, y),
en este caso la ecuaci´on diferencial que cumple la condici´on es:
dy
dx
=
y
x
que es una ecuaci´on de variable separable, solucionandola obtenemos la
familia de trayectorias ortogonales:
y = Cx

7. TRAYECTORIAS ORTOGONALES EJEMPLOS
EJEMPLOS
EJEMPLO
FIGURA: En la figura se observan la familia de circunferencias dada en el ejercicio y la familia de rectas obtenidas como trayectorias
ortogonales.

8. BIBLIOGRAF´IA
ZILL, D., CULLEN, M., Ecuaciones diferenciales con problemas con valores
en la frontera, octava edici´on, Cengage Learning, Mexico, DF, 2014.
BOYCE, W., DIPRIMA, R., Elementary Differential Equation and Boundary
Value problems, Novena edici´on, JohnWiley and Sons, Inc. USA, 2009.
NAGLE, R.K., SAFF, E.B., Fundamentos de Ecuaciones Diferenciales, Addison-
Wesley, Iberoamericana, 1992.
POLKING, J., BOGGESS, A., ARNOLD, D., Differential equations with boun-
dary value problems, Segunda edici´on, Pearson Prentice Hall, 2005.