1. Un vector de posición localiza un punto en el espacio con respecto a otro punto.
2. La manera más fácil de formular las componentes de un vector de posición consiste en determinar la distancia y la dirección que debe recorrerse a lo largo de las direcciones x, y, z desde la cola hasta la cabeza del vector.
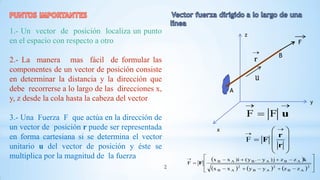
3. Una fuerza F que actúa en la dirección de un vector de posición r puede ser representada en forma cartesiana si se determina el vector unitario u del vector de posición y éste se multiplica por la magnitud de