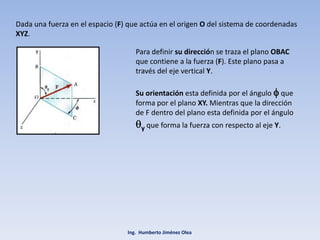
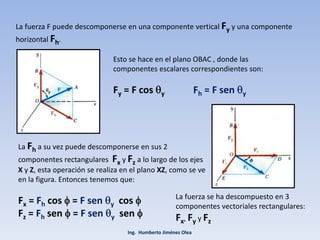
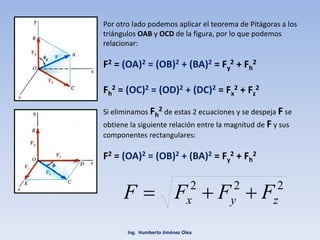
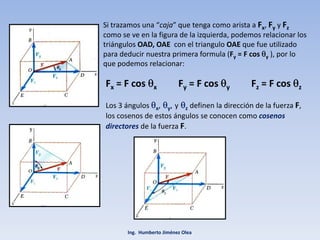
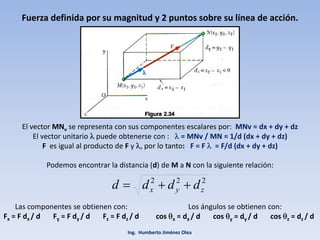
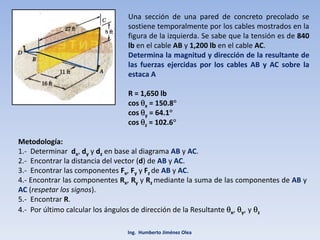
El documento describe los métodos para descomponer una fuerza en el espacio en componentes rectangulares y determinar su dirección. Se explica cómo descomponer una fuerza en tres componentes ortogonales Fx, Fy y Fz usando ángulos. También se presentan fórmulas para calcular la magnitud de una fuerza a partir de sus componentes y para sumar fuerzas en el espacio.

1. Ing. Humberto Jiménez Olea

2. Dada una fuerza en el espacio (F) que actúa en el origen O del sistema de coordenadas
XYZXYZ.
Para definir su dirección se traza el plano OBAC
que contiene a la fuerza (F). Este plano pasa a
é d l j i l Ytravés del eje vertical Y.
Su orientación esta definida por el ángulo φ que
forma por el plano XY Mientras que la direcciónforma por el plano XY. Mientras que la dirección
de F dentro del plano esta definida por el ángulo
θy que forma la fuerza con respecto al eje Y.
Ing. Humberto Jiménez Olea

3. La fuerza F puede descomponerse en una componente vertical Fy y una componente
horizontal Fh.
Esto se hace en el plano OBAC , donde las
componentes escalares correspondientes son:componentes escalares correspondientes son:
Fy = F cos θy Fh = F sen θy
La Fh a su vez puede descomponerse en sus 2
componentes rectangulares Fx y Fz a lo largo de los ejes
X y Z esta operación se realiza en el plano XZ como se veX y Z, esta operación se realiza en el plano XZ, como se ve
en la figura. Entonces tenemos que:
Fx = Fh cos φ = F sen θy cos φ La fuerza se ha descompuesto en 3
componentes vectoriales rectangulares:x h φ y φ
Fz = Fh sen φ = F sen θy sen φ
componentes vectoriales rectangulares:
Fx, Fy y Fz
Ing. Humberto Jiménez Olea

4. Por otro lado podemos aplicar el teorema de Pitágoras a los
triángulos OAB y OCD de la figura por lo que podemostriángulos OAB y OCD de la figura, por lo que podemos
relacionar:
F2 = (OA)2 = (OB)2 + (BA)2 = Fy
2 + Fh
2( ) ( ) ( ) y h
Fh
2 = (OC)2 = (OD)2 + (DC)2 = Fx
2 + Fz
2
Si eliminamos Fh
2 de estas 2 ecuaciones y se despeja F se
obtiene la siguiente relación entre la magnitud de F y sus
componentes rectangulares:componentes rectangulares:
F2 = (OA)2 = (OB)2 + (BA)2 = Fy
2 + Fh
2
222
zyx FFFF ++= y
Ing. Humberto Jiménez Olea

5. Si trazamos una “caja” que tenga como arista a Fx, Fy y Fz
como se ve en la figura de la izquierda podemos relacionar loscomo se ve en la figura de la izquierda, podemos relacionar los
triángulos OAD, OAE con el triangulo OAE que fue utilizado
para deducir nuestra primera formula (Fy = F cos θy ), por lo
que podemos relacionar:
Fx = F cos θx Fy = F cos θy Fz = F cos θz
3 á l θ θ θ d fi l di ió d l f FLos 3 ángulos θx, θy, y θz definen la dirección de la fuerza F,
los cosenos de estos ángulos se conocen como cosenos
directores de la fuerza F.
Ing. Humberto Jiménez Olea

6. Ejercicio 1:
Una fuerza de 500N forma ángulos de 60°, 45° y 120° con los ejes X, Y y Z respectivamente.
E l F F F d l fEncuentra las componentes Fx, Fy y Fz de la fuerza.
Resultado: Fx = 250N, Fy = 354 N, Fz = ‐250 N
Relaciones de los Cosenos DirectoresRelaciones de los Cosenos Directores
(cos θx)2 + (cos θy)2 + (cos θz)2 = 1
cos θx = Fx / F cos θy = Fy / F cos θz = Fz / F
Ejercicio 2:
Una fuerza de F tiene las componentes Fx = 20 lb, Fy ‐30 lb y Fz = 60 lb. Determina la p x , y y z
magnitud de F y los angulos θx, θy, y θz que forman con los ejes de coordenadas.
Respuestas: F = 70 lb, θx = 73.4°, θy = 115.4°, y θz = 31°

7. Fuerza definida por su magnitud y 2 puntos sobre su línea de acción.
El vector MNv se representa con sus componentes escalares por: MNv = dx + dy + dz
El vector unitario λ puede obtenerse con : λ = MNv / MN = 1/d (dx + dy + dz)El vector unitario λ puede obtenerse con : λ = MNv / MN = 1/d (dx + dy + dz)
F es igual al producto de F y λ, por lo tanto: F = F λ = F/d (dx + dy + dz)
Podemos encontrar la distancia (d) de M a N con la siguiente relación:
222
zyx dddd ++=
Los ángulos se obtienen con:Las componentes se obtienen con: Los ángulos se obtienen con:
cos θx = dx / d cos θy = dy / d cos θz = dz / d
Las componentes se obtienen con:
Fx = F dx / d Fy = F dy / d Fz = F dz / d
Ing. Humberto Jiménez Olea

8. El alambre de una torre esta anclado en A por
medio de un perno, la tensión en el alambre es
d 2 500 Nde 2,500 N.
Determine las componentes Fx, Fy y Fz de la
fuerza que actúa sobre el perno. Los ángulos θx,
θy, y θz que definen la dirección de la fuerza.θy, y θz que definen la dirección de la fuerza.
Resultado:
Fx = –1 060 N
F 2 120 N
cos θx = 115.1°
θ 32°Fy = 2,120 N
Fz = 795 N
cos θy = 32°
cos θz = 71.5°
Metodología:
1.‐ Determinar dx, dy y dz en base al diagrama.y
2.‐ Encontrar la distancia del vector (d).
3.‐ Encontrar las componentes Fx, Fy y Fz.
4.‐ Por último calcular los ángulos de dirección de la fuerza θx, θy, y θz
Ing. Humberto Jiménez Olea

9. Adicción de fuerzas en el espacio.
La resultante es la suma de 2 o más fuerza en el espacioLa resultante es la suma de 2 o más fuerza en el espacio.
R = ΣF
La resultante R de 2 o más fuerzas en el espacio se calcula sumando sus componentes
rectangulares.rectangulares.
R = Rx + Ry + Rz
Para determinar las componentes de la fuerza resultante tenemos que:
Rx = ΣFx Ry = ΣFy Rz = ΣFzRx ΣFx Ry ΣFy Rz ΣFz
La magnitud de la resultante y los ángulos de dirección en el espacio con respecto a los ejes
de coordenadas con las siguientes relaciones:
222
zyx RRRR ++=
cos θx = Rx / R cos θy = Ry / R cos θz = Rz / R
Ing. Humberto Jiménez Olea

10. Una sección de una pared de concreto precolado se
sostiene temporalmente por los cables mostrados en la
fi d l i i d S b l t ió d 840figura de la izquierda. Se sabe que la tensión es de 840
lb en el cable AB y 1,200 lb en el cable AC.
Determina la magnitud y dirección de la resultante de
las fuerzas ejercidas por los cables AB y AC sobre la
estaca A
R = 1,650 lb
cos θ = 150 8°cos θx = 150.8
cos θy = 64.1°
cos θz = 102.6°
Metodología:
1.‐ Determinar dx, dy y dz en base al diagrama AB y AC.
2.‐ Encontrar la distancia del vector (d) de AB y AC.
3 ‐ Encontrar las componentes F F y F de AB y AC3. Encontrar las componentes Fx, Fy y Fz de AB y AC.
4.‐ Encontrar las componentes Rx, Ry y Rz mediante la suma de las componentes de AB y
AC (respetar los signos).
5.‐ Encontrar R.
4.‐ Por último calcular los ángulos de dirección de la Resultante θx, θy, y θz
Ing. Humberto Jiménez Olea