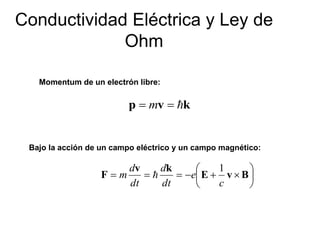
Este documento trata sobre la conductividad eléctrica y la ley de Ohm. Explica que bajo la acción de un campo eléctrico y magnético, la variación del momento de un electrón libre es proporcional al campo eléctrico. También introduce la ley de Ohm, que establece que la densidad de corriente es directamente proporcional al campo eléctrico aplicado, y define la conductividad eléctrica. Además, discute conceptos como la resistividad eléctrica, el tiempo libre medio y

1. Conductividad Eléctrica y Ley de
Ohm
Momentum de un electrón libre:
p  mv  k
Bajo la acción de un campo eléctrico y un campo magnético:



d
d
    E  v B

v k
F
c
e
dt
dt
m
1


2. B = 0
k(t)  k(0)  eEt / 
k  eEt / 

7. B = 0
k(t)  k(0)  eEt / 
k  eEt / 

8. v  eE /m
nq ne /m 2 j  v  E
Ley de Ohm
Conductividad eléctrica
j E
Ejemplo de ecuación
material
ne 
m

2


9. Resistividad eléctrica:
m
 2 ne



11. El parámetro  el tiempo libre promedio durante el cual el campo
eléctrico actúa sobre el portador.
La trayectoria libre media:  F v l 
A bajas temperaturas, las colisiones son con impurezas y otras
imperfecciones.
A temperatura ambiente con fonones.

12. Resistividad Eléctrica Experimental
de los Metales





m
   


m
m
     

L i ne
ne
L i L i
ne
  
1 1
2 2 2
Resistividad residual

13. Regla de Matthiessen
• La resistividad en presencia de varios
mecanismos de dispersión distintos es
simplemente la suma de las resistividades que
se tendrían si estuviera presente cada una por
separado.
---Ejemplo. La dispersión por impurezas puede ser
independiente de la temperatura.
---La interacción electrón electrón si depende de la
temperatura.

14. • El cociente de resistividad se define como
el cociente entre de la resistividad a
temperatura ambiente y la resistividad
residual.
• Es una estimación aproximada de la
pureza de la muestra.