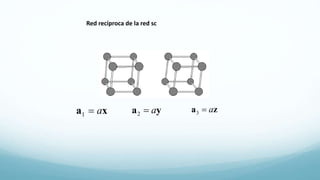
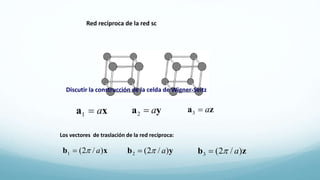
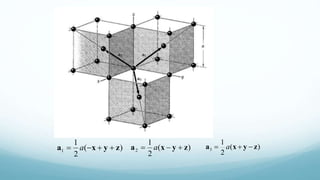
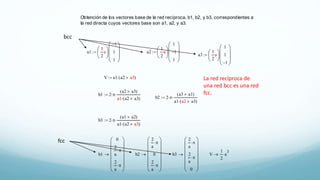
Este documento presenta el temario de un curso sobre estado sólido II. Los temas incluyen la red recíproca y determinación de estructuras por difracción de rayos X, enlace cristalino, gas de Fermi de electrones libres y niveles electrónicos en un potencial periódico. El profesor expondrá los temas y los estudiantes resolverán problemas representativos. Las evaluaciones incluyen exámenes parciales, tareas y exposiciones.

1. ESTADO SÓLIDO II.
V.2015.012H
Prof. Rodolfo Bernal

2. TEMARIO:
La Red Recíproca y Determinación de Estructuras por Difracción de
Rayos X.
Enlace Cristalino.
Gas de Fermi de Electrones Libres.
Niveles Electrónicos en un Potencial Periódico. Propiedades Generales.

3. ESTADO SÓLIDO II
Modalidades de los Procesos de Enseñanza y Aprendizaje.
Exposición de los temas por parte del profesor.
Resolución y discusión en clase de algunos problemas representativos.
El estudiante deberá complementar su dominio del material de cada tema
resolviendo una serie de problemas modelo que serán cuidadosamente
seleccionados por el profesor.

4. BIBLIOGRAFÍA MÍNIMA:
Charles Kittel. Introduction to Solid State Physics. Eighth Edition. John
Wiley & Sons, New York. 2005.
Neil W. Ashcroft, N. David Mermin. Solid State Physics. Saunders College
Publishing (1976).

5. EVALUACIÓN Y ACREDITACIÓN:
Exámenes parciales: 60 %.
Tareas: 30 %.
Exposiciones: 10 %.

9. E 1 100
Para los fotones: Para neutrones: Para electrones:
 E( )
12.4
E

n E( )
2.86
E
 e E( )
1.2226
E

1 10 100
0.1
1
10
100
12.4
0.122
 E( )
n E( )
e E( )
1001 E
rayos X
neutrones
electrones

10. Difracción de ondas por cristales
 Cuando la longitud de onda de la radiación incidente es del orden o
menor que la constante de red se puede observar la difracción. Por
eso no es de esperarse la difracción de cristales usando luz visible.
 El haz difractado se observa cuando las reflexiones de planos
paralelos de átomos interfieren constructivamente. Cada plano
contribuye con una fracción muy pequeña.

11. La red recíproca

12. Difracción de rayos X

14. Difracción de ondas por cristales
 Cada plano refleja 10-3 a 10-5 de la radiación incidente, de manera que de
103 a 105 planos paralelos pueden contribuir al haz reflejado en un cristal
perfecto.
 La ley de Bragg es una consecuencia de la periodicidad de la red.
 La composición de la base asociada a cada punto de red determina la
intensidad de la difracción.

15. Amplitud dispersada
 La ley de Bragg establece la condición para que ocurra la interferencia
constructiva de ondas dispersadas por los puntos de red.
 Es necesario un análisis más a fondo para determinar la intensidad
dispersada en función de la base asociada a los puntos de red, es decir, a
partir de la distribución espacial de los electrones en una celda.

16. Una estructura cristalina tiene la propiedad de invarianza
Traslacional, bajo traslaciones de la forma:
332211 aaaT uuu 
Cualquier propiedad física local es entonces invariante
traslacionalmente.

17. Análisis de Fourier
FC f N L( ) R
0 
1
2 L L
L
xf x( )



d
0











R n 
1
L
L
L
xf x( ) cos
n  x
L











d
1
L
L
L
xf x( ) sin
n  x
L











d



















n 1 Nfor
R
T

Ao no
Bn Sp
An Cp

18. Análisis de Fourier
p x( ) A0
1
N
n
An cos
n  x
L






 Bn sin
n  x
L















1 0 1
1
0
1
2
Periodic function
Nth Fourier polynomial
2
1
f x( )
p x( )
LL x
1 0 1
1
0
1
2
Periodic function
Nth Fourier polynomial
2
1
f x( )
p x( )
LL x
N=1
N=5
1 0 1
1
0
1
2
Periodic function
Nth Fourier polynomial
2
1
f x( )
p x( )
LL x
N=30
L x L :
f x( ) 1 0 x 1if
x 1 x 0if
f x 2( ) x 1if


19. Análisis de Fourier
 En particular, la densidad electrónica n (r ) es una
función periódica de r, con periodicidades a lo largo de
los ejes cristalinos a1, a2 y a3.
)()( rTr nn 
• Las propiedades más interesantes de los
cristales están directamente relacionadas con las
componentes de Fourier de la densidad
electrónica.

20. Análisis de Fourier
Enter a function that is periodic on interval:
n(x) = no + Cp cos(2p px / a)+Spsen(2πpx / a)éë ùû
p>0
å
p x( ) A0
1
N
n
An cos
n  x
L






 Bn sin
n  x
L















  )()2sen()2/2cos()(
0
xnppx/a2SpapxCnaxn
p
ppo  


21. Análisis de Fourier
ap/2Se dice que el punto
es un punto en la red recíproca o el espacio de
Fourier del cristal.
Los puntos de la red recíproca son los términos permitidos en la serie de
Fourier, que son consistentes con la periodicidad del cristal.

22. Red recíproca en 1D

23. 
p
apxi
penxn /2
)( 
pnn p

*
P enteros negativos, enteros negativos y 0.
Para garantizar que n sea real.



a
apxi
p exdxn
a
n
0
/2
)(
1 

24. En tres dimensiones:
El conjunto de vectores G debe de ser tal que n es invariante bajo
Cualquier traslación cristalina T que deja al cristal invariante.
El conjunto de coeficientes de Fourier nG determina la amplitud
de la dispersión de rayos X.
 

G
rG
Gr i
enn )(

25. f N L( ) R
0 
1
2 L L
L
xf x( )



d
0











R n 
1
L
L
L
xf x( ) cos
n  x
L











d
1
L
L
L
xf x( ) sin
n  x
L











d



















n 1 Nfor
R
T




a
apxi
p exdxn
a
n
0
/2
)(
1 

26. 


a
apxi
p exdxn
a
n
0
/2
)(
1 
Vcell es el volumen de una celda del cristal.



cell
)(
1
dVen
V
n i
c
rG
G r

27. 
p
apxi
penxn /2
)( 



a
apxi
p exdxn
a
n
0
/2
)(
1 
Coeficientes de Fourier

28. Vectores de la red recíproca
321
32
1 2
aaa
aa
b


 
321
13
2 2
aaa
aa
b


 
321
21
3 2
aaa
aa
b


 
Si los vectores a son vectores
Primitivos de la red cristalina,
Los vectores b son vectores
Primitivos de la red recíproca.

29. ijji 2ab
332211 bbbG vvv 
Los puntos en la red recíproca:
Un vector G es un vector de la red recíproca.

30.   
G
rG
G
G
TGrG
GTr )()( rneneenn iii
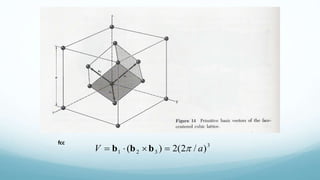
332211 bbbG vvv 
1)(2
)]()([
332211
332211332211




vuvuvui
uuuvvvii
e
ee

aaabbbTG

31. Red Recíproca
 Cada estructura cristalina tiene dos redes asociadas: la red cristalina y la
red recíproca.
 El patrón de difracción de un cristal es un mapa de la red recíproca del
cristal.
 Una imagen de microscopia electrónica, en caso de poder resolverse, es
un mapa de la estructura cristalina en el espacio real.

32. Red Recíproca
 Ambas redes están relacionadas, de manera que si rotamos un cristal,
rotamos tanto la red real como la red recíproca.

33. Análisis dimensional
 Los vectores en la red directa tienen unidad de [L].
 Los vectores en la red recíproca tienen unidades de [1/L].
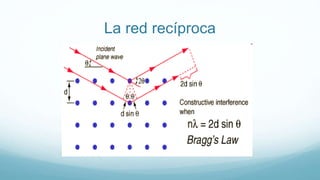
 La red recíproca es una red en el espacio de Fourier asociado con el
cristal.

34. Condiciones de difracción
 Teorema: El conjunto de vectores G de la red recíproca determina las
reflexiones de rayos X.

35. Red recíproca de la red sc
xa a1
ya a2
za a3

36. 321
32
1 2
aaa
aa
b


 
321
13
2 2
aaa
aa
b


 
321
21
3 2
aaa
aa
b


 

37. Red recíproca de la red sc
xa a1
ya a2
za a3
Los vectores de traslación de la red recíproca:
xb )/2(1 a yb )/2(2 a zb )/2(3 a
Discutir la construcción de la celda de Wigner-Seitz

39. Obtención de los vectores base de la red recíproca, b1, b2, y b3, correspondientes a
la red directa cuyos vectores base son a1, a2, y a3.
a1
a
0
0









a
a2
0
a
0








 a a3
0
0
a









a
b1 2 
a2 a3( )
a1 a2 a3( )

a1 b2 2 
a3 a1( )
a1 a2 a3( )

a2
b3 2 
a1 a2( )
a1 a2 a3( )

a3
b1
2
a

0
0








 b2
0
2
a

0








 b3
0
0
2
a











40. Red recíproca de la red bcc

42. )(
2
1
1 zyxa  a )(
2
1
2 zyxa  a )(
2
1
3 zyxa  a

43. 321
32
1 2
aaa
aa
b


 
321
13
2 2
aaa
aa
b


 
321
21
3 2
aaa
aa
b


 

44. Obtención de los vectores base de la red recíproca, b1, b2, y b3, correspondientes a
la red directa cuyos vectores base son a1, a2, y a3.
a1
1
2
a





1
1
1








 a a2
1
2
a





1
1
1








 a
a3
1
2
a





1
1
1








 a
V a1 a2 a3( ) a3
b1 2 
a2 a3( )
a1 a2 a3( )

a1 b2 2 
a3 a1( )
a1 a2 a3( )

a2
b3 2 
a1 a2( )
a1 a2 a3( )

a3
b1
0
2
a

2
a















 b2
2
a

0
2
a















 b3
2
a

2
a

0














 V
1
2
a
3

bcc
fcc
La red recíproca de
una red bcc es una red
fcc.

45. fcc 3
321 )/2(2)( aV  bbb

46.  zyxbbbG )()()()
2
( 213132332211 vvvvvv
a
vvv 

La forma general de un vector de la red recíproca:
Los G’s más cortos posibles:
)(
2
)(
2
)(
2
yxzxzy 

















aaa


47. Primera zona de Brillouin de la red bcc. Se contruye la celda
de Wigner-Seitz de una fcc. La figura es un dodecaedro
(poliedro de doce caras planas) rómbico regular.
Los vectores desde el origen al centro de cada cara son:
)()()( yxzxzy 

















aaa


48. Red recíproca de una red fcc
)(
2
1
1 zya  a
)(
2
1
2 zxa  a
)(
2
1
3 yxa  a

49. 321
32
1 2
aaa
aa
b


 
321
13
2 2
aaa
aa
b


 
321
21
3 2
aaa
aa
b


 

50. Obtención de los vectores base de la red recíproca, b1, b2, y b3, correspondientes a
la red directa cuyos vectores base son a1, a2, y a3.
a1
a
2
1





0
1
1









a
a2
a
2
1





1
0
1









a
a3
a
2
1





1
1
0









a
V a1 a2 a3( ) a3
b1 2 
a2 a3( )
a1 a2 a3( )

a1 b2 2 
a3 a1( )
a1 a2 a3( )

a2
b3 2 
a1 a2( )
a1 a2 a3( )

a3
b1
2
a

2
a

2
a

















 b2
2
a

2
a

2
a

















 b3
2
a

2
a

2
a

















 V
1
4
a
3

)(
2
)(
2
)(
2
321 zyxbzyxbzyxb 


















aaa

)(
2
1
1 zya  a )(
2
1
2 zxa  a )(
2
1
3 yxa  a
fcc
bcc !!
3
321 )/2(4)( aV  bbb

51. Los vectores G más cortos:
 zyxbbbG  )
2
(332211
a
vvv

Las fronteras de la celda central

52. )(
2
1
1 zyxa  a )(
2
1
2 zyxa  a )(
2
1
2 zyxa  a
bcc
Las fronteras de la celda central
están determinadas por 8 planos
normales a estos vectores en
sus puntos medios.
También hay cortes de los
planos que son bisectores
perpendiculares de otros 6
vectores de la red recíproca.
)2(
2
)2(
2
)2(
2
3 zbyx 

















aaa


53. bcc
Zona de Brillouin de una red fcc. Las celdas están en el espacio
Recíproco, y la red recíproca es bcc.