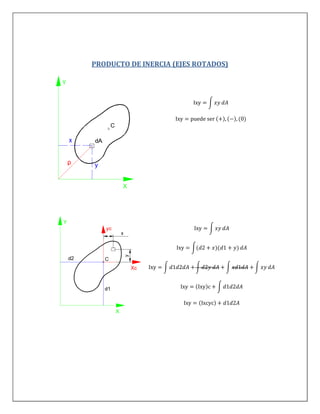
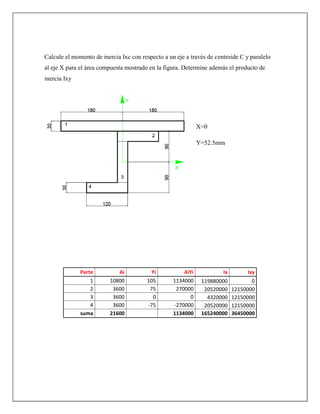
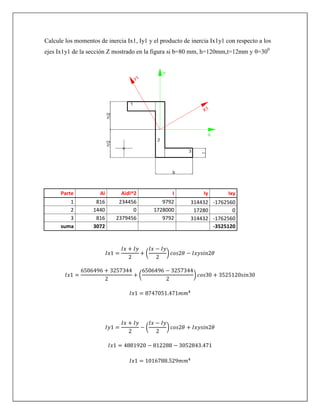
Este documento trata sobre los productos de inercia y los ejes rotados. Explica cómo calcular los productos de inercia Ixcyc con respecto a los ejes centroidales y cómo rotar los ejes para determinar los nuevos momentos de inercia. También cubre los conceptos de ejes y puntos principales, y cómo calcular los momentos de inercia principales I1 e I2. Finalmente, incluye ejercicios de aplicación para practicar estos cálculos.

1. UNIVERSIDAD TÉCNICA DE AMBATO
FACULTAD DE INGENIERÍA CIVIL Y MECÁNICA
CARRERA DE INGENIERÍA MECÁNICA
SISTEMAS MECÁNICOS II
TEMA:
PRODUCTOS DE INERCIA
EJES ROTADOS
DOCENTE:
Ing. Mg. Segundo Espín
Septiembre 2013

2. PRODUCTO DE INERCIA (EJES ROTADOS)
∫
( ) ( ) ( )
∫
∫( )( )
∫ ∫ ∫ ∫
( ) ∫
( )

3. ROTACIÓN DE EJES
∫
∫( )
( )
( )
( )
( ) ( )
( )
( )

4. PRODUCTOS DE INERCIA (EJES ROTADOS)
∫
( )( )
( )
( )
( )

5. Ejercicios De Aplicación
Determine el producto de inercia Ixcyc con respecto a los ejes centroidales xc, yc, paralelos
a los ejes xy respectivamente para el aria en forma
de L mostrada en la figura
AT=A1+A2
AT=3+1.75
AT=4.75in2
( ) ( )
( )
( )
( ) ( )
( )
( )
( ) ( ) ( )
( )
( )
( ) ( )
( ) ( )
( )
( )

6. Calcule el momento de inercia Ixc con respecto a un eje a través de centroide C y paralelo
al eje X para el área compuesta mostrado en la figura. Determine además el producto de
inercia Ixy
X=0
Y=52.5mm
Parte Ai Yi AiYi Ix Ixy
1 10800 105 1134000 119880000 0
2 3600 75 270000 20520000 12150000
3 3600 0 0 4320000 12150000
4 3600 -75 -270000 20520000 12150000
suma 21600 1134000 165240000 36450000

7. Calcule los momentos de inercia Ix1, Iy1 y el producto de inercia Ix1y1 con respecto a los
ejes Ix1y1 de la sección Z mostrado en la figura si b=80 mm, h=120mm,t=12mm y θ=300
Parte Ai Aidi^2 I Iy Ixy
1 816 234456 9792 314432 -1762560
2 1440 0 1728000 17280 0
3 816 2379456 9792 314432 -1762560
suma 3072 -3525120
( )
( )
( )

8. ( )( )
( )( )
EJES PRINCIPALES
 Uno de los ejes es principal si es simétrico
 Si parte del mismo origen del eje principal también es principal
 Sí tiene el mismo momento de inercia que en el centroide también es principal
PUNTOS PRINCIPALES
Un punto localizado de tal manera que cada eje a través del punto sea un eje principal y por
consiguiente los momentos de inercia sean los mismos para todos los ejes a través del punto
se llama punto principal

9. Reglas Para Puntos Principales
a) Los ejes principales que pasan por el origen so un par de ejes ortogonales para los
cuales los momentos de inercia son máximo y un mínimo
b) La orientación de los ejes principales está dada por el ángulo θp obtenido con
ecuación
c) El producto de inercia es cero para los ejes principales
d) El eje de simetría siempre es un eje principal

10. MOMENTOS DE INERCIA PRINCIPALES
Es de más inseguro o de mayor peligro
√( ) ( )
√( ) ( )

11. Ejercicios de aplicación
Determine los ángulos θp1 y θp2 que definían las orientaciones de los ejes principales a
través del origen para el triángulo mostrado en la figura si b=6in, h=8in. También calcule
los correspondientes momentos de inercia principales I1 e I2
Ix=256in4
Iy=144in4
Ixy=96in4
√( ) ( )
√( ) ( )
√( ) ( )
√( ) ( )

12. ( )
( ) ( ) ( )
Determine los ángulos θp1 y θp2 que definen las orientaciones de los ejes centroidales
principales y los momentos de inercia I1, I2 correspondientes para el área en forma de L de
la figura si a=80mm, b=150mm, t=16mm
x=54.96in
y=19.96in
Parte Ai Yi xi AiXi AiYi Ixi Iyi dy dx Ai*di^2 Ai*di^2
1,00 1280,00 40,00 8,00 10240,00 51200,00 682666,67 27306,67 20,04 46,96 513896,15 2823069,91
2,00 2144,00 8,00 83,00 177952,00 17152,00 45738,67 3208138,67 11,96 28,04 306835,06 1685341,30
suma 3424,00 68352,00 728405,33 3235445,33 820731,22 4508411,22
Ix1=1549136.549
Iy1=7743856.549