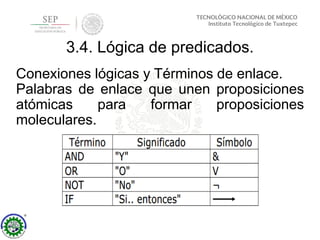
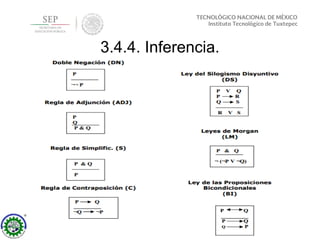
Este documento presenta la unidad III sobre inteligencia artificial de la carrera de Ingeniería en Sistemas Computacionales. Explica conceptos clave de lógica de predicados como términos, constantes, funciones, variables, predicados, átomos y literales. También describe la sintaxis y semántica de la lógica de predicados, incluyendo interpretaciones, dominios y validez de predicados.

1. Unidad III
“INTELIGENCIA ARTIFICIAL”
CARRERA:
Ingeniería en Sistemas Computacionales
FECHA DE ENTREGA
lunes, 25 de mayo de 2015
PRESENTA:
Chalate Jorge Humberto
Gaspar Rufino M. del Rosario
Hernández García Nidia M.
Juárez Martínez Esmeralda
Ortiz Andrés Erika
8° Semestre Grupo “A”
S.E.P. D.G.E.S.T. S.N.E.S.T.
INSTITUTO TECNOLÓGICO de Tuxtepec
M.S.C. TOMÁS TORRES RAMÍREZ

2. 3.4. Lógica de predicados.

3. 3.4. Lógica de predicados.
Es una herramienta para estudiar el
comportamiento de un sistema lógico.
Además proporciona un criterio para
determinar si un sistema lógico es absurdo o
inconsistente.
Sistema simbólico: Lenguaje y fórmulas
lógicas

4. 3.4. Lógica de predicados.
Proposiciones.
Representación en lenguaje cotidiano
que debe estar libre de vaguedades.

5. 3.4. Lógica de predicados.
Conexiones lógicas y Términos de enlace.
Palabras de enlace que unen proposiciones
atómicas para formar proposiciones
moleculares.

6. 3.4. Lógica de predicados.
Simbolización de proposiciones.
Uso de variables para representar proposiciones.
P = "Se cerró el circuito"
Q = "Operó la marcha"
P & Q = "Se cerró el circuito y operó la marcha"
¬Q = "No operó la marcha“

7. 3.4.1. Sintaxis.Elementos.
• Términos: Representan objetos del
dominio.
• Constantes: Representan un objeto
individual en concreto notación: cadenas
de caracteres, comienzan en mayúsculas
notación: cadenas de caracteres, comienzan
en mayúsculas
Ejemplos: Juan; Mi coche;…

8. 3.4.1. Sintaxis.
• Funciones: Representan (implícitamente) un
objeto individual que está relacionado con los n
objetos que participan en la función
notación: símbolo de función (cadena, comienza
con Mays.) con aridad n + n argumentos (términos)
entre paréntesis
Ejemplos: Padre de (Juan); Hijo de (Pedro; Ana);
Coseno (45)…

9. 3.4.1. Sintaxis.
• Variables: Representan objetos sin indicar
cuales.
• Predicados: Representan una propiedad de un
término (si aridad 1) o relaciones entre k
términos (si aridad k > 1)
notación: cadenas de caracteres + k términos
(variables, constantes, funciones) entre paréntesis.

10. 3.4.1. Sintaxis.
• Átomos: formulas bien formadas (f. b. f.)
compuestas por un único predicado
• Literales: Átomo o negación de un átomo.
Ejemplos: Asesina (Juan; x); Es_alto (Juan);
Vive_con (Juan; Padre_de (Juan));…

11. 3.4.2. Semántica.
Representamos un mundo donde hay:
• Un n° infinito de objetos individuales
representados por símbolos de constantes y
variables.
Pueden ser entidades concretas (personas, cosas)
o abstractas(números, eventos).

12. 3.4.2. Semántica.
• Un n° infinito de objetos de nidos en
función de otros objetos, representados
por símbolos de función.
Relaciones entre los objetos del dominio,
representadas por símbolos de predicado.
Si la aridad es 1, se habla de propiedades de
objetos.

13. 3.4.2. Semántica.
Interpretaciones.
Una interpretación establece las relaciones
anteriores entre los símbolos de la lógica y los
elementos del mundo real
• asocia a las constantes objetos del mundo
• asocia a las funciones relaciones funcionales
entre objetos
• asocia a los predicados relaciones entre objetos
Más compleja que en lógica de proposiciones.

14. 3.4.2. Semántica.
Dominio de una interpretación: Conjunto de objetos
del mundo que se manejan en una interpretación
Formalmente: Dada una conceptualización formada
por:
• U: universo de discurso (conj. de
individuos/objetos)
• R: conj. Finito de relaciones entre objetos de U
• F: conj. Finito de funciones que asocian a 1
objetos de U con 1 o más objetos de U

15. 3.4.3. Validez.
• Un predicado con variables libres no es
verdadero ni falso, hasta que se asignen valores
para dichas variables.
• Algunos de ellos serán siempre verdaderos
independientemente de los valores que se
escojan: estos son predicados válidos.
• Un predicado que es verdadero o falso
dependiendo de los valores elegidos se dice que
es satisfacible.
• Un predicado que es siempre falso se dice que
es no satisfacible.

16. 3.4.4. Inferencia.
Reglas de inferencia:

17. 3.4.4. Inferencia.