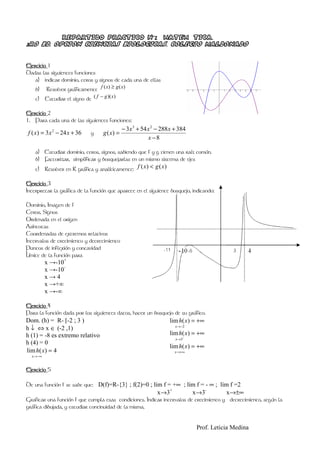
Este documento presenta 5 ejercicios de matemática que involucran funciones. El Ejercicio 1 pide estudiar dominios, ceros y signos de funciones f(x) y g(x), y resolver gráficamente f(x) ≥ g(x) y el signo de (f-g)(x). El Ejercicio 2 involucra funciones f(x) y g(x) con una raíz común y pide factorizar, simplificar, bosquejar y resolver gráficamente y analíticamente f(x) < g(x). El Ejercicio 3

1. REPARTIDO PRACTICO Nº2 MATEM TICA.
3RO BD. OPCION CIENCIAS BIOLOGICAS. COLEGIO MALDONADO
Ejercicio 1
Dadas las siguientes funciones
a) indicar dominio, ceros y signos de cada una de ellas
b) Resolver gráficamente f ( x) ≥ g ( x)
c) Estudiar el signo de ( f − g )( x)
Ejercicio 2
1. Para cada una de las siguientes funciones:
− 3 x 3 + 54 x 2 − 288 x + 384
f ( x) = 3 x 2 − 24 x + 36 y g ( x) =
x −8
a) Estudiar dominio, ceros, signos, sabiendo que f y g tienen una raíz común.
b) Factorizar, simplificar y bosquejarlas en un mismo sistema de ejes
c) Resolver en R gráfica y analíticamente: f ( x) < g ( x )
Ejercicio 3
Interpretar la gráfica de la función que aparece en el siguiente bosquejo, indicando:
Dominio, Imagen de f
Ceros, Signos
Ordenada en el origen
Asíntotas
Coordenadas de extremos relativos
Intervalos de crecimiento y decrecimiento
Puntos de inflexión y concavidad
Límite de la función para
x →-10+
x →-10-
x→4
x →+∞
x →-∞
Ejercicio 4
Para la función dada por los siguientes datos, hacer un bosquejo de su gráfico.
Dom. (h) = R- [-2 ; 3 ) lim h( x ) = +∞
h ↓ ⇔ x ∈ (-2 ,1) x→−2
h (1) = -8 es extremo relativo lim h( x) = +∞
x→3−
h (4) = 0
lim h( x ) = +∞
lim h( x) = 4 x→+∞
x→−∞
Ejercicio 5
De una función f se sabe que: D(f)=R-{3} ; f(2)=0 ; lím f = +∞ ; lím f = - ∞ ; lím f =2
x→3+ x→3- x→±∞
Graficar una función f que cumpla esas condiciones. Indicar intervalos de crecimiento y decrecimiento, según la
gráfica dibujada, y estudiar continuidad de la misma.
Prof. Leticia Medina