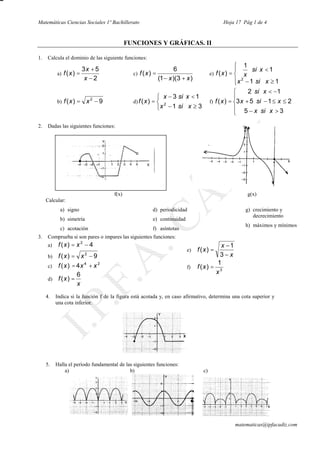
Este documento presenta varios ejercicios sobre funciones y gráficas. Se piden calcular dominios, estudiar propiedades como simetría, monotonía, acotación y extremos de funciones, hallar composiciones y precomposiciones de funciones, y completar gráficas de funciones periódicas. Los ejercicios abarcan una amplia gama de conceptos relacionados con funciones y su representación gráfica.

1. Matemáticas Ciencias Sociales 1º Bachillerato Hoja 17 Pág 1 de 4
matematicas@ipfacadiz.com
FUNCIONES Y GRÁFICAS. II
1. Calcula el dominio de las siguiente funciones:
a)
2
53
)(
+
=
x
x
xf c)
)3)(1(
6
)(
xx
xf
+
= e)
<
=
11
1
1
)(
2
xsix
xsi
xxf
b) 9)( 2
= xxf d)
<
=
31
13
)( 2
xsix
xsix
xf f)
>
+
<
=
35
2153
12
)(
xsix
xsix
xsi
xf
2. Dadas las siguientes funciones:
f(x) g(x)
Calcular:
a) signo
b) simetría
c) acotación
d) periodicidad
e) continuidad
f) asíntotas
g) crecimiento y
decrecimiento
h) máximos y mínimos
3. Comprueba si son pares o impares las siguientes funciones:
a) 4)( 2
= xxf
b) 9)( 2
= xxf
c)
24
4)( xxxf +=
d)
x
xf
6
)( =
e)
x
x
xf =
3
1
)(
f) 3
1
)(
x
xf =
4. Indica si la función f de la figura está acotada y, en caso afirmativo, determina una cota superior y
una cota inferior.
5. Halla el período fundamental de las siguientes funciones:
a) b) c)

2. Matemáticas Ciencias Sociales 1º Bachillerato Hoja 17 Pág 2 de 4
matematicas@ipfacadiz.com
6. Estudia la acotación de la función f:
7. Estudia la simetría de las siguientes funciones:
a) b) c)
8. Estudia la monotonía y los extremos de las siguientes funciones:
9. Estudia la simetría, la monotonía y los extremos de la función f:
10. Completa las siguientes gráficas de forma par o impar según se indique:
11. Completa las gráficas sabiendo que son periódicas de periodo T.

3. Matemáticas Ciencias Sociales 1º Bachillerato Hoja 17 Pág 3 de 4
matematicas@ipfacadiz.com
12. Si f(x) = 3x – 5 y g(x) = 1/x , ¿cuánto vale f(4)?¿Yg(7)? Calcula g(f(4)) y g(f(x)). ¿Cuál es la
función fg o ? ¿Y la función gf o ?
13. Calcula gf o y fg o para las siguientes funciones:
a) f(x) = x2
y g(x) = cos x b) xxf =)( y
4
1
)( 2
=
x
xg
14. Dadas las funciones f(x) = x + 3 , g(x) = 2x – 7 , h(x) = 5 – 3x, se pide:
a) Calcular [fog](x).
b) Calcular [g of](x).
c) Probar que [fog] oh = fo[goh]
d) Probar que [fog] –1
= g –1
o f –1
e) Probar que [fog] –1
f –1
o g
–1
Soluciones.
1. a) R-{2}; b) ] [ )+,33,( ; c) R-{-3,1};
d) [ )+,3)1,( ; e) R-{0}; f) ] ),3(2,( +
2. f(x)
a) f positiva si ( )5,3'2)2,4(x ;
f negativa si )3'2,2(x ;
f nula si x = -4, -2 ó 2’3
b) no tiene simetrías (ni par ni impar)
c) acotada superiormente por 2 e inferiormente por
–2
d) No es periódica
e) Es continua en su dominio
f) No tiene asíntotas
g) f es creciente si )3,2()7'2,4(x ;
f decreciente si )5,3()1,7'2(x
h) Max en x =3 y min en [ ]2,1x
g(x)
a) f positiva si ( )2,0)0,(x ;
f negativa si ),4()4,2( +x ;
f nula si x =2 ó 4
b) no tiene simetrías (ni par ni impar)
c) No está acotada ni superiormente ni
inferiormente
d) No es periódica
e) Es discontinua en x =0 y x =4
f) Asíntotas verticales en x = 0 y x = 4
g) f es creciente si )0,2(x ;
f decrec si ),4()4,0()2,( +x
h) min en x = -2
3. a) par b) par c) par d) impar e) no tiene simetrías f) impar
4. Acotada superiormente por 2 e inferiormente por –1.
5. a) T = 2 ; b) T = 2 ; c) T = 4.
6. Acotada. Cota superior: 2; cota inferior: 0
7. a) Función par. Simétrica respecto de OY. b) Función impar. Simétrica respecto de O. c) No es simétrica.
8. a) Creciente en ( )1, ; decreciente en ( ) ( )+,11,1 ;máximo local en x = -1 y su valor es 2; no tiene ni
máximo absoluto ni mínimo absoluto.
b) Creciente en ( )1,3 ; decreciente en ( ) ( )+,13, ;máximo local en x = 1 y su valor es 3; mínimo local
en x = -3 y su valor es -2; no tiene ni máximo absoluto ni mínimo absoluto.
c) Creciente en ( ) ( )+,22,4 ; decreciente en ( )4, ;mínimo local en x = -4 y su valor es 2; no tiene
ni máximo absoluto ni mínimo absoluto.

4. Matemáticas Ciencias Sociales 1º Bachillerato Hoja 17 Pág 4 de 4
matematicas@ipfacadiz.com
9. Función par: Simétrica respecto del eje OY. Creciente en ( )+,0 y decreciente en ( )0, . Mínimo absoluto en
x = 0. Función acotada.
10.
11.
12. . f(4) = 7 ; g(7) = 1/7 ; g(f(4)) = 1/7 ; g(f(x))=
53
1
x
;
53
1
))(( =
x
xfg o ; ( ) 5
3
)( =
x
xgf o
13. a) ( ) xxgf 2
cos)( =o ; ( ) )cos()( 2
xxfg =o ; b) ( )
4
1
)( 2
=
x
xgf o ; ( )
4
1
)( =
x
xfg o
14.
a) [fog](x) = 2x – 4
b) [gof](x) = 2x – 1
c) [fog] oh = fo[goh] = 6 – 6x
d) [fog] –1
= g –1
o f –1
=
2
4+x
e) f –1
o g –1
=
2
1+x
[fog] –1