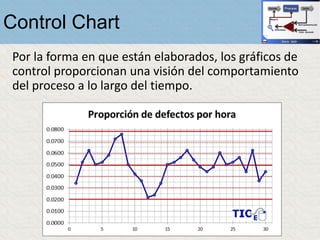
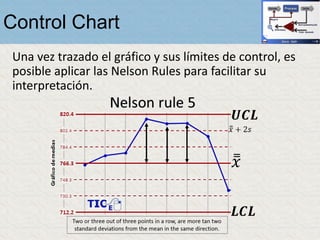
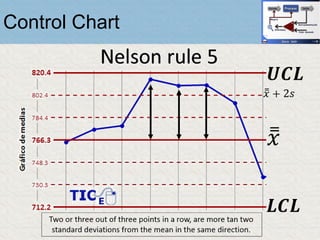
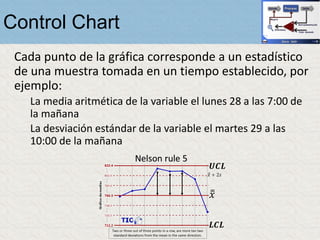
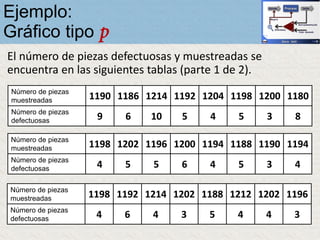
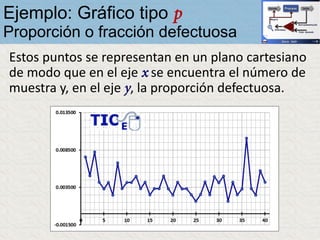
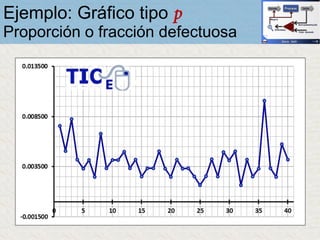
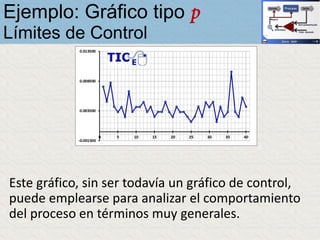
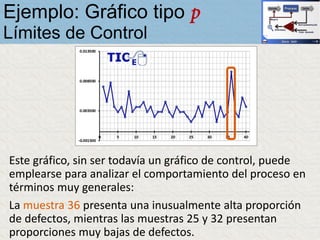
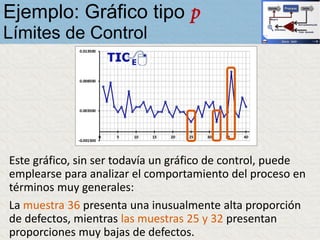
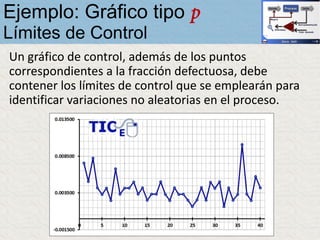
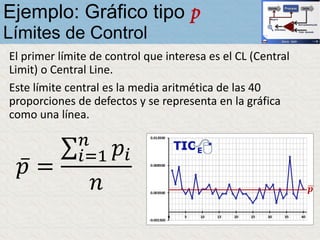
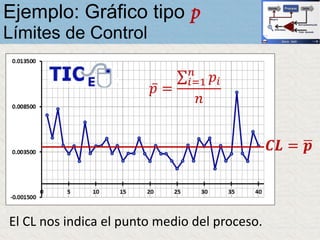
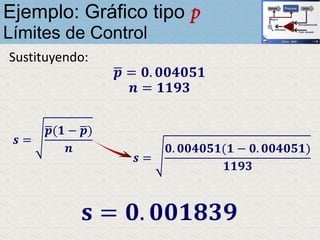
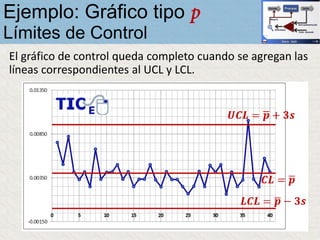
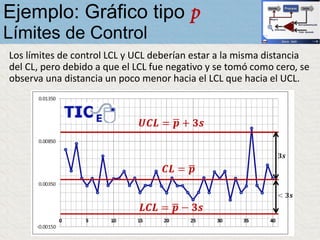
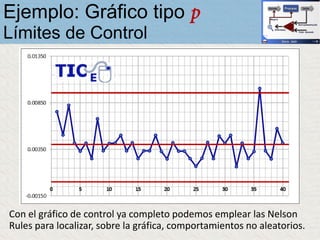
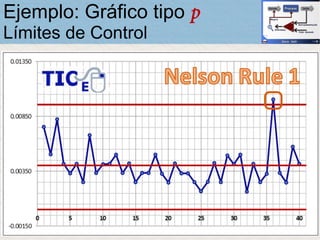
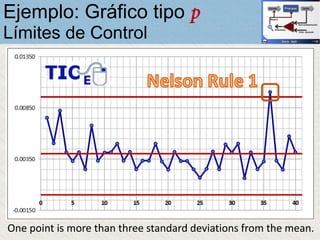
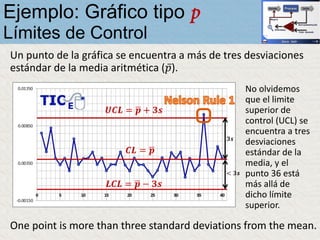
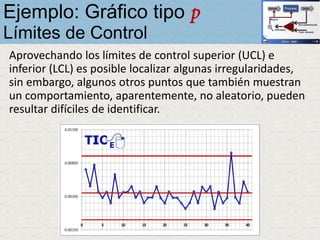
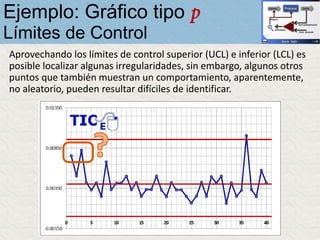
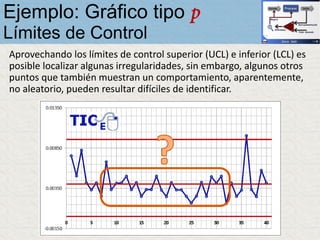
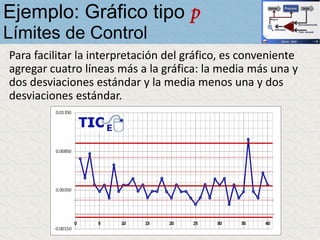
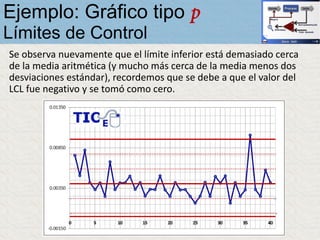
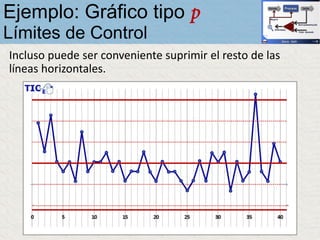
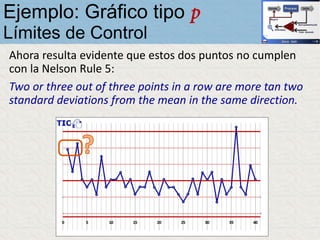
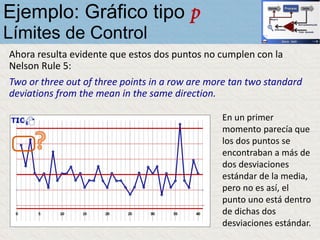
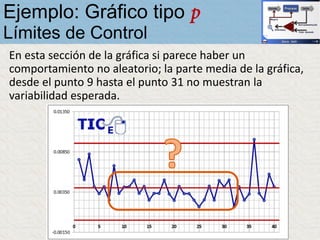
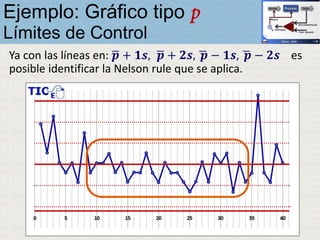
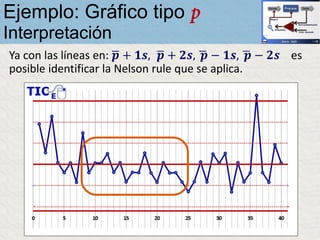
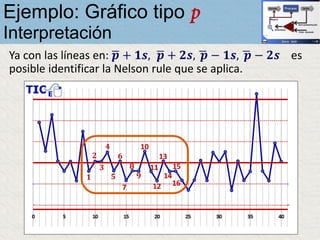
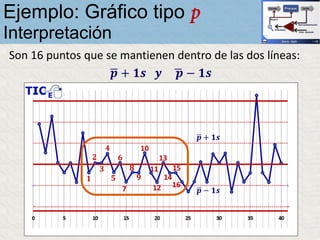
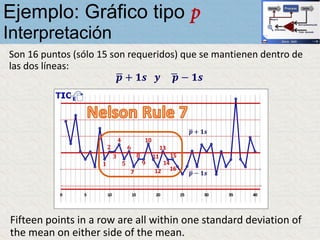
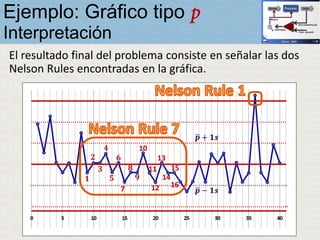
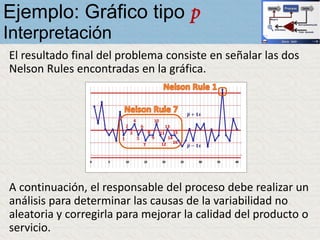
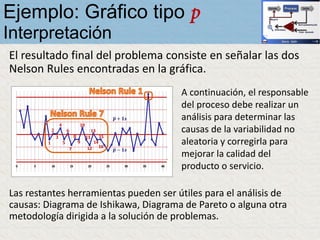
El documento describe un gráfico de control tipo p para monitorear la calidad de obleas de semiconductores. Se midió la proporción de obleas defectuosas en 40 muestras tomadas cada hora. Se calculó la media de las proporciones, la desviación estándar y los límites de control superior e inferior. El gráfico muestra que un punto está fuera del límite superior, indicando una variación no aleatoria en el proceso.

1. Seven Basic Tools of Quality: Control Charts Introduction (p chart).
G. Edgar Mata Ortiz

2. Control Chart
¿Qué es un gráfico de control?
Es una de las 7 herramientas básicas para la
calidad
Está formado por las medias aritméticas,
rangos, desviaciones estándar u otros
estadísticos de un conjunto de muestras
tomadas a intervalos regulares en el tiempo;
cada hora, cada 4 horas, cada turno, o
cualquier otra secuencia sistemática.

3. Control Chart
Su característica más sobresaliente son los límites
de control, tres líneas principales y cuatro
secundarias que nos permiten identificar
variaciones no aleatorias en un proceso.
Límites de control

4. Control Chart
¿Por qué son importantes las variaciones no
aleatorias de un proceso?
Cualquier proceso presenta variabilidad; los
pequeños cambios que ocurren en los diferentes
factores de la producción o el servicio no pueden
ser evitados y afectan a la calidad.

5. Control Chart
Sin embargo, cuando estos cambios no son
aleatorios, es posible determinar sus causas y
eliminarlos para reducir la variabilidad y mejorar la
calidad del producto o servicio.

6. Control Chart
Por la forma en que están elaborados, los gráficos de
control proporcionan una visión del comportamiento
del proceso a lo largo del tiempo.

7. Control Chart
Una vez trazado el gráfico y sus límites de control, es
posible aplicar las Nelson Rules para facilitar su
interpretación.

8. Control Chart

9. Control Chart
Cada punto de la gráfica corresponde a un estadístico
de una muestra tomada en un tiempo establecido, por
ejemplo:
La media aritmética de la variable el lunes 28 a las 7:00 de
la mañana
La desviación estándar de la variable el martes 29 a las
10:00 de la mañana

10. Control Chart
Por las características de los datos se dispone de
dos tipos de gráfico de control.

11. Control Chart
Gráficos de control para variables.
Los gráficos de control para variables
se elaboran con estadísticos como la
media aritmética, el rango y la
desviación estándar.
Los más usuales son:
1. Gráfica de medias y rangos
2. Gráfica de medias y desviaciones
estándar.

12. Control Chart
Gráficos de control para atributos.
Los gráficos de control para atributos
se construyen empleando
proporciones, porcentajes,
fracciones.
Los más usuales son:
1. Gráfica tipo p, np, 100p
2. Gráfico tipo c
3. Gráfico tipo u

13. Ejemplo:
Gráfico de Control para Atributos
En una fábrica de semiconductores el espesor de
las obleas es una característica de calidad.

14. Ejemplo:
Gráfico de Control para atributos
• Este espesor debe ser de 11 ± 1 milésimas de
pulgada.

15. Ejemplo:
Gráfico de Control para atributos
Con la finalidad de
determinar la
proporción de
obleas que no
cumplen con las
especificaciones, se
ha decidido tomar
40 muestras; una
cada hora durante
los próximos 5
turnos de 8 horas
de operación.

16. Ejemplo:
Gráfico tipo p
El número de piezas defectuosas y muestreadas se
encuentra en las siguientes tablas (parte 1 de 2).
Número de piezas
muestreadas 1190 1186 1214 1192 1204 1198 1200 1180
Número de piezas
defectuosas 9 6 10 5 4 5 3 8
Número de piezas
muestreadas 1198 1202 1196 1200 1194 1188 1190 1194
Número de piezas
defectuosas 4 5 5 6 4 5 3 4
Número de piezas
muestreadas 1198 1192 1214 1202 1188 1212 1202 1196
Número de piezas
defectuosas 4 6 4 3 5 4 4 3

17. El número de piezas defectuosas obtenidas y muestreadas
se encuentra en las siguientes tablas (parte 2 de 2).
Número de piezas
muestreadas 1198 1180 1176 1194 1008 1210 1194 1210
Número de piezas
defectuosas 2 3 5 3 5 5 6 2
Número de piezas
muestreadas 1192 1194 1214 1192 1196 1202 1216 1194
Número de piezas
defectuosas 5 3 4 12 4 3 7 5
Ejemplo:
Gráfico tipo p

18. Ejemplo: Gráfico tipo p
Proporción o fracción defectuosa
• La fracción defectuosa o proporción defectuosa se
obtiene dividiendo, para cada muestra, el número de
piezas defectuosas, entre el número de piezas
muestreadas.
• Por ejemplo, para la muestra 1 tenemos:
𝒑 =
Número de piezas defectuosas
Número de piezas muestreadas
𝒑 =
𝟗
𝟏𝟏𝟗𝟎
→ 𝒑 = 𝟎. 𝟎𝟎𝟕𝟓𝟔

19. • Con esta fórmula se calculan las proporciones de
defectos de todas la muestras.
1 1190 9 0.007563
2 1186 6 0.005059
3 1214 10 0.008237
4 1192 5 0.004195
5 1204 4 0.003322
35 1214 4 0.003295
36 1192 12 0.010067
37 1196 4 0.003344
38 1202 3 0.002496
39 1216 7 0.005757
40 1194 5 0.004188
…
Ejemplo: Gráfico tipo p
Proporción o fracción defectuosa

20. Estos puntos se representan en un plano cartesiano
de modo que en el eje x se encuentra el número de
muestra y, en el eje y, la proporción defectuosa.
Ejemplo: Gráfico tipo p
Proporción o fracción defectuosa

21. Ejemplo: Gráfico tipo p
Proporción o fracción defectuosa

22. Este gráfico, sin ser todavía un gráfico de control,
puede emplearse para analizar el comportamiento
del proceso en términos muy generales.
Ejemplo: Gráfico tipo p
Límites de Control

23. Este gráfico, sin ser todavía un gráfico de control, puede
emplearse para analizar el comportamiento del proceso en
términos muy generales:
La muestra 36 presenta una inusualmente alta proporción
de defectos, mientras las muestras 25 y 32 presentan
proporciones muy bajas de defectos.
Ejemplo: Gráfico tipo p
Límites de Control

24. Este gráfico, sin ser todavía un gráfico de control, puede
emplearse para analizar el comportamiento del proceso en
términos muy generales:
La muestra 36 presenta una inusualmente alta proporción
de defectos, mientras las muestras 25 y 32 presentan
proporciones muy bajas de defectos.
Ejemplo: Gráfico tipo p
Límites de Control

25. Un gráfico de control, además de los puntos
correspondientes a la fracción defectuosa, debe
contener los límites de control que se emplearán para
identificar variaciones no aleatorias en el proceso.
Ejemplo: Gráfico tipo p
Límites de Control

26. El primer límite de control que interesa es el CL (Central
Limit) o Central Line.
Este límite central es la media aritmética de las 40
proporciones de defectos y se representa en la gráfica
como una línea.
ҧ𝑝 =
σ𝑖=1
𝑛
𝑝𝑖
𝑛
Ejemplo: Gráfico tipo p
Límites de Control

27. El CL nos indica el punto medio del proceso.
Ejemplo: Gráfico tipo p
Límites de Control

28. Para calcular el valor de ഥ𝒑 es necesario sumar las 40
proporciones defectuosas y dividir el resultado
entre 40.
ഥ𝒑 =
𝟎. 𝟏𝟔𝟐𝟎𝟓
𝟒𝟎
El valor de n es el tamaño de muestra promedio, es
necesario sumar todos los tamaños de muestra,
dividir entre las 40 muestras y redondear.
𝒏 =
𝟒𝟕𝟕𝟎𝟎
𝟒𝟎
Ejemplo: Gráfico tipo p
Límites de Control

29. En este ejemplo el valor de la proporción media de
defectos es:
ഥ𝒑 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏
El valor de n es el tamaño de muestra promedio:
𝒏 = 𝟏𝟏𝟗𝟑
Estos valores se emplean para determinar la
desviación estándar:
Ejemplo: Gráfico tipo p
Límites de Control
𝒔 =
ഥ𝒑(𝟏 − ഥ𝒑)
𝒏

30. En este ejemplo el valor de la proporción media de
defectos es:
ഥ𝒑 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏
El valor de n es el tamaño de muestra promedio:
𝒏 = 𝟏𝟏𝟗𝟑
𝒔 =
ഥ𝒑(𝟏 − ഥ𝒑)
𝒏
𝒔 =
𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏(𝟏 − 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏)
𝟏𝟏𝟗𝟑
Ejemplo: Gráfico tipo p
Límites de Control

31. Sustituyendo:
ഥ𝒑 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏
𝒏 = 𝟏𝟏𝟗𝟑
𝒔 =
ഥ𝒑(𝟏 − ഥ𝒑)
𝒏
𝒔 =
𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏(𝟏 − 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏)
𝟏𝟏𝟗𝟑
Ejemplo: Gráfico tipo p
Límites de Control

32. La proporción media de defectos más el triple
de la desviación estándar es el UCL (Upper
Control Limit) o límite superior de control:
ഥ𝒑 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏
𝒔 = 𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗
𝐔𝐂𝐋 = ഥ𝒑 + 𝟑𝒔 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 + 𝟑(𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗)
Ejemplo: Gráfico tipo p
Límites de Control

33. La proporción media de defectos más el triple de la
desviación estándar es el UCL (Upper Control Limit)
o límite superior de control:
𝐔𝐂𝐋 = ഥ𝒑 + 𝟑𝒔 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 + 𝟑(𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗)
𝐔𝐂𝐋 = 𝟎. 𝟎𝟎𝟗𝟓𝟔𝟖
Ejemplo: Gráfico tipo p
Límites de Control

34. La proporción media de defectos menos el triple de
la desviación estándar es el LCL (Lower Control
Limit) o límite inferior de control:
Ejemplo: Gráfico tipo p
Límites de Control
ഥ𝒑 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏
𝒔 = 𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗
𝐋𝐂𝐋 = ഥ𝒑 − 𝟑𝒔 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 − 𝟑(𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗)

35. La proporción media de defectos menos el triple de
la desviación estándar es el LCL (Lower Control
Limit) o límite inferior de control:
𝐋𝐂𝐋 = ഥ𝒑 − 𝟑𝒔 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 − 𝟑(𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗)
𝐋𝐂𝐋 = −𝟎. 𝟎𝟎𝟏𝟒𝟔𝟔
Ejemplo: Gráfico tipo p
Límites de Control

36. La proporción media de defectos menos el triple de
la desviación estándar es el LCL (Lower Control
Limit) o límite inferior de control:
𝐋𝐂𝐋 = ഥ𝒑 − 𝟑𝒔 = 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 − 𝟑(𝟎. 𝟎𝟎𝟏𝟖𝟑𝟗)
𝐋𝐂𝐋 = −𝟎. 𝟎𝟎𝟏𝟒𝟔𝟔
Cuando el límite inferior de control es negativo se
toma igual a cero:
𝐋𝐂𝐋 = 𝟎
Ejemplo: Gráfico tipo p
Límites de Control

37. El gráfico de control queda completo cuando se agregan las
líneas correspondientes al UCL y LCL.
Ejemplo: Gráfico tipo p
Límites de Control

38. Los límites de control LCL y UCL deberían estar a la misma distancia
del CL, pero debido a que el LCL fue negativo y se tomó como cero, se
observa una distancia un poco menor hacia el LCL que hacia el UCL.
Ejemplo: Gráfico tipo p
Límites de Control

39. Con el gráfico de control ya completo podemos emplear las Nelson
Rules para localizar, sobre la gráfica, comportamientos no aleatorios.
Ejemplo: Gráfico tipo p
Límites de Control

40. Ejemplo: Gráfico tipo p
Límites de Control

41. One point is more than three standard deviations from the mean.
Ejemplo: Gráfico tipo p
Límites de Control

42. Un punto de la gráfica se encuentra a más de tres desviaciones
estándar de la media aritmética ( ҧ𝑝).
No olvidemos
que el limite
superior de
control (UCL) se
encuentra a tres
desviaciones
estándar de la
media, y el
punto 36 está
más allá de
dicho límite
superior.
One point is more than three standard deviations from the mean.
Ejemplo: Gráfico tipo p
Límites de Control

43. Aprovechando los límites de control superior (UCL) e
inferior (LCL) es posible localizar algunas irregularidades,
sin embargo, algunos otros puntos que también muestran
un comportamiento, aparentemente, no aleatorio, pueden
resultar difíciles de identificar.
Ejemplo: Gráfico tipo p
Límites de Control

44. Aprovechando los límites de control superior (UCL) e inferior (LCL) es
posible localizar algunas irregularidades, sin embargo, algunos otros
puntos que también muestran un comportamiento, aparentemente,
no aleatorio, pueden resultar difíciles de identificar.
Ejemplo: Gráfico tipo p
Límites de Control

45. Aprovechando los límites de control superior (UCL) e inferior (LCL) es
posible localizar algunas irregularidades, sin embargo, algunos otros
puntos que también muestran un comportamiento, aparentemente,
no aleatorio, pueden resultar difíciles de identificar.
Ejemplo: Gráfico tipo p
Límites de Control

46. Para facilitar la interpretación del gráfico, es conveniente
agregar cuatro líneas más a la gráfica: la media más una y
dos desviaciones estándar y la media menos una y dos
desviaciones estándar.
Ejemplo: Gráfico tipo p
Límites de Control

47. Se observa nuevamente que el límite inferior está demasiado cerca
de la media aritmética (y mucho más cerca de la media menos dos
desviaciones estándar), recordemos que se debe a que el valor del
LCL fue negativo y se tomó como cero.
Ejemplo: Gráfico tipo p
Límites de Control

48. Incluso puede ser conveniente suprimir el resto de las
líneas horizontales.
Ejemplo: Gráfico tipo p
Límites de Control

49. Ahora resulta evidente que estos dos puntos no cumplen
con la Nelson Rule 5:
Two or three out of three points in a row are more tan two
standard deviations from the mean in the same direction.
Ejemplo: Gráfico tipo p
Límites de Control

50. Ahora resulta evidente que estos dos puntos no cumplen con la
Nelson Rule 5:
Two or three out of three points in a row are more tan two standard
deviations from the mean in the same direction.
En un primer
momento parecía que
los dos puntos se
encontraban a más de
dos desviaciones
estándar de la media,
pero no es así, el
punto uno está dentro
de dichas dos
desviaciones estándar.
Ejemplo: Gráfico tipo p
Límites de Control

51. En esta sección de la gráfica si parece haber un
comportamiento no aleatorio; la parte media de la gráfica,
desde el punto 9 hasta el punto 31 no muestran la
variabilidad esperada.
Ejemplo: Gráfico tipo p
Límites de Control

52. Ya con las líneas en: ഥ𝒑 + 𝟏𝒔, ഥ𝒑 + 𝟐𝒔, ഥ𝒑 − 𝟏𝒔, ഥ𝒑 − 𝟐𝒔 es
posible identificar la Nelson rule que se aplica.
Ejemplo: Gráfico tipo p
Límites de Control

53. Ya con las líneas en: ഥ𝒑 + 𝟏𝒔, ഥ𝒑 + 𝟐𝒔, ഥ𝒑 − 𝟏𝒔, ഥ𝒑 − 𝟐𝒔 es
posible identificar la Nelson rule que se aplica.
Ejemplo: Gráfico tipo p
Interpretación

54. Ya con las líneas en: ഥ𝒑 + 𝟏𝒔, ഥ𝒑 + 𝟐𝒔, ഥ𝒑 − 𝟏𝒔, ഥ𝒑 − 𝟐𝒔 es
posible identificar la Nelson rule que se aplica.
Ejemplo: Gráfico tipo p
Interpretación

55. Son 16 puntos que se mantienen dentro de las dos líneas:
ഥ𝒑 + 𝟏𝒔 𝒚 ഥ𝒑 − 𝟏𝒔
Ejemplo: Gráfico tipo p
Interpretación

56. Son 16 puntos (sólo 15 son requeridos) que se mantienen dentro de
las dos líneas:
ഥ𝒑 + 𝟏𝒔 𝒚 ഥ𝒑 − 𝟏𝒔
Fifteen points in a row are all within one standard deviation of
the mean on either side of the mean.
Ejemplo: Gráfico tipo p
Interpretación

57. El resultado final del problema consiste en señalar las dos
Nelson Rules encontradas en la gráfica.
Ejemplo: Gráfico tipo p
Interpretación

58. El resultado final del problema consiste en señalar las dos
Nelson Rules encontradas en la gráfica.
A continuación, el responsable del proceso debe realizar un
análisis para determinar las causas de la variabilidad no
aleatoria y corregirla para mejorar la calidad del producto o
servicio.
Ejemplo: Gráfico tipo p
Interpretación

59. El resultado final del problema consiste en señalar las dos
Nelson Rules encontradas en la gráfica.
Las restantes herramientas pueden ser útiles para el análisis de
causas: Diagrama de Ishikawa, Diagrama de Pareto o alguna otra
metodología dirigida a la solución de problemas.
Ejemplo: Gráfico tipo p
Interpretación
A continuación, el responsable
del proceso debe realizar un
análisis para determinar las
causas de la variabilidad no
aleatoria y corregirla para
mejorar la calidad del
producto o servicio.

60. Ejemplo: El Gráfico tipo p
El gráfico que se ha tomado como ejemplo es un
gráfico tipo p, de fracción defectuosa o de
proporción defectuosa.
Si se desea facilitar la comprensión y la
interpretación, pueden multiplicarse todos los
valores por 100, obteniéndose así porcentaje de
piezas defectuosas.
En tal caso el gráfico recibe el nombre de:
Gráfico tipo 100p

61. Ejemplo: El Gráfico tipo 100p
Si se desea facilitar la comprensión y la interpretación,
puede multiplicarse la escala del eje y por 100,
obteniéndose así porcentaje de piezas defectuosas.
En tal caso el gráfico recibe el nombre de:
Gráfico tipo 100p
En este ejemplo, si empleamos un gráfico 100p, la tasa
media de defectos sería:
Y podemos expresar, en forma más intuitiva que la
tasa de defectos es del 0.4051%
ഥ𝒑 = 𝟏𝟎𝟎 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 = 𝟎. 𝟒𝟎𝟓𝟏

62. Ejemplo: El Gráfico tipo 1000p
Si la multiplicación por cien sigue arrojando valores muy
pequeños y se desea hacerlos más intuitivos, podemos
multiplicar por mil. En tal caso podemos nombrar el gráfico
como:
Gráfico tipo 1000p
En este ejemplo, si empleamos un gráfico al que llamamos
1000p, la tasa media de defectos sería:
Y podemos expresar, en forma más intuitiva, que la
tasa de defectos es de 4.051 defectos por cada mil
piezas producidas.
ഥ𝒑 = 𝟏𝟎𝟎𝟎 𝟎. 𝟎𝟎𝟒𝟎𝟓𝟏 = 𝟒. 𝟎𝟓𝟏

63. Gracias por su atención
• Referencias:
http://www.scoop.it/t/mathematics-learning
https://sites.google.com/site/mataspc/home
http://licmata-math.blogspot.com/
http://www.slideshare.net/licmata/
http://www.facebook.com/licemata
licmata@hotmail.com
Twitter: @licemata