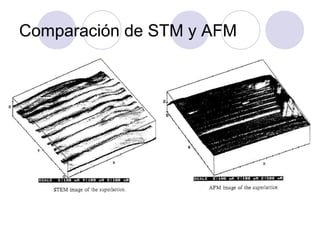
El documento explora el estudio de superredes mediante microscopía de fuerza de fricción y técnicas relacionadas como AFM, destacando aspectos como la caracterización de nanotubos de carbono, la adhesión y fricción en monocapas orgánicas, y los solitones en fullerenos. Se presentan métodos para evaluar propiedades de fractura, corrosión y orden espontáneo en superredes, así como comparaciones entre diferentes técnicas de microscopía. Finalmente, se discuten aplicaciones y efectos en diversas estructuras y materiales como capas delgadas y puntos cuánticos.

1. Estudio de superredes
mediante AFM
Javier García Molleja

2. Introducción
 Microscopía de fuerza de fricción
 Monocapas orgánicas
 Nanotubos de carbono
 Solitones en fullerenos
 Efectos de la corrosión
 Efectos del orden espontáneo
 Películas delgadas de óxido de perovskita

3. Introducción
 Caracterizaciónde antipuntos
 Propiedades de fractura
 Superred de CoO/Co
 Puntos cuánticos en superredes
 Comparación de STM y AFM

4. Microscopía de fuerza de fricción
 Al estudiar con AFM el grafito aparece el
efecto conocido como “stick-slip” (o
elevación-deslizamiento).
 En este efecto aparecerán saltos de la
punta y por tanto no podrán determinarse
completamente las estructuras atómicas.

5. Microscopía de fuerza de fricción

6. Microscopía de fuerza de fricción
 Para evitar el efecto haremos el estudio
desde el punto de vista de la fricción
lateral.
 Se considerarán para ello distintas
combinaciones de rigidez lateral y carga
normal en el cantilever.

7. Microscopía de fuerza de fricción
 El cantilever puede sufrir los siguientes
movimientos:
1. Doblamiento vertical
2. Doblamiento lateral
3. Torsión
4. Extensión

8. Microscopía de fuerza de fricción

9. Microscopía de fuerza de fricción
 El modelo analítico de estudio se basa en
la suposición de un comportamiento
similar a muelles elásticos.
 Analizaremos en detalle los grados de
libertad y la composición de movimientos.
 Así se simularán diferentes
comportamientos atendiendo a la
deflexión o no del cantilever.

10. Microscopía de fuerza de fricción
 En el modo de fuerza constante se tiene que θYC
es constante, por lo que para conocer f Y hay que
medir θxC.
 Si no se considera la dinámica del cantilever
deberá cumplirse que el movimiento de éste sea
más lento que las vibraciones de la red.
 Debemos apoyarnos de estudios cuánticos y
moleculares. Supondremos que el potencial de
interacción es del tipo de Lennard-Jones.

11. Microscopía de fuerza de fricción
 Al no considerar la dinámica se podrá
observar que la posición de los átomos de
carbono no es exacta al estudiar el mapa
de fuerza lateral.
 El mapa de fuerza normal sí dará las
posiciones exactas.
 Esto se debe a la coincidencia o no del
máximo de fuerza y la posición.

12. Microscopía de fuerza de fricción

13. Microscopía de fuerza de fricción
 Podemos también considerar la dinámica del
cantilever.
 Necesitamos un tratamiento matricial para la
ecuación de movimiento.
 La masa, la rigidez y la fuerza de interacción
entre punta y muestra serán matrices.
 El vector de desplazamiento absoluto y relativo
también se relacionan por una matriz.

14. Microscopía de fuerza de fricción

15. Monocapas orgánicas
 Con AFM se pueden realizar estudios
tribológicos.
 El sustrato será de Si (111) y se
depositará por evaporación una capa de
Au (111).
 El oro se limpia con radiación y soluciones
químicas.

16. Monocapas orgánicas
 Si sumegimos todo el sistema en soluciones
orgánicas, con el tiempo se creará una capa de
tipo orgánico.
 El entrecruzamiento entre las moléculas se
puede lograr con un bombardeo electrónico.
 El estudio se hará en modo contacto con
inclinación de 22º y un 45-55% de humedad
relativa, limpiando previamente la muestra con
agua destilada.

17. Monocapas orgánicas

18. Monocapas orgánicas
 Punta y cantilever son de Si3N4, con el
último recubierto de oro, forma triangular y
constante 0.58 N/m. La punta será una
pirámide cuadrada de 30-50 nm de radio.
 Obtendremos las imágenes de rugosidad
y fricción. La adhesión se determinará en
el modo de calibración.
 Se recurre a una punta de base triangular
de diamante para realizar el desgaste.

19. Monocapas orgánicas
 Con las dimensiones del cantilever y su
módulo de Young podemos determinar la
constante de muelle.
 La punta recorrerá periódicamente una
muestra de silicio para eliminar la posible
contaminación.
 Podemos estudiar el efecto de la
humedad.

20. Monocapas orgánicas
 Existe
una buena correlación entre las
imágenes de altura y fricción, ya que
cambian al unísono.

21. Monocapas orgánicas

22. Monocapas orgánicas
 La
adhesión se puede modelizar con F L =
2πRγla (cosθ1 + cosθ2).
R es el radio de la gota de agua de forma
esférica, γla es la tensión del líquido contra
el aire y los valores θ1 y θ2 son los ángulos
de contacto entre el líquido y superficies
planas y esféricas, respectivamente.

23. Monocapas orgánicas
 Mediante la ecuación de Young-Dupre
sabremos el trabajo de adhesión: Wa = γla
(1 + cos θ1).

24. Monocapas orgánicas

25. Monocapas orgánicas
 Las figuras muestran los mapas de fricción y de
desgaste.
 Los resultados dependen del empaquetamiento
molecular de cada capa depositada.
 Se comprueba que existe un valor crítico.
 La adhesión y la fricción aumentan por la
creación de un capilar de agua en presencia de
los grupos polares, a humedad relativa distinta
de cero.

26. Nanotubos de carbono
 Se sintetizan a partir de una plantilla de
policarbonato tras un tratamiento
electroquímico. Posteriormente, se elimina
la plantilla con una solución.
 Todo el sistema se filtra con una
membrana porosa, por lo que los
nanotubos quedarán en los poros.

27. Nanotubos de carbono

28. Nanotubos de carbono
 El cantilever será de Si3N4.
 Las propiedades físicas se determinan por
la frecuencia de resonancia del cantilever
libre.
 Entre el portamuestras y la punta se
aplicará un campo eléctrico modulado,
pero sin imponer polarización.
 Esto hace que el pico de resonancia sea
simétrico.

29. Nanotubos de carbono
 Los nanotubos se detectan al aumentar la
frecuencia de resonancia respecto a la
que posee el cantilever aislado.
 La deformación y la contribución del
nanotubo hacen cambiar el valor de la
frecuencia.
 Aparecerá en el diagrama tres picos de
vibración: dos de flexión del cantilever y
otro de torsión.

30. Nanotubos de carbono

31. Nanotubos de carbono
 La frecuencia de resonancia dependerá
del diámetro y la longitud suspendida (o
sea, rigidez) del nanotubo.
 El estudio del fenómeno se hace con un
modelo de muelles.
 Mostrará el modelo la deformación del
nanotubo en las dos dimensiones.

32. Nanotubos de carbono

33. Nanotubos de carbono
 La componente paralela de deformación
depende de la orientación relativa
respecto del cantilever.
 La componente angular es bastante
grande, pudiendo entonces despreciar la
anterior.
 El modelo predice que la rigidez entre
punta y nanotubo es mayor que la natural
del último.

34. Nanotubos de carbono
 Con el modelo podemos determinar el
módulo elástico.
 Para ello hay que describir las
condiciones de contorno (el anclaje) y la
frecuencia de resonancia.

35. Solitones en fullerenos
 Un solitón es una onda que no se
amortigua al propagarse por un medio no
lineal.
 El medio de propagación puede ser el C 70,
que se crea por el método del transporte
de polvo al sufrir un lento descenso de la
temperatura.
 Estudiaremos el medio con AFM.

36. Solitones en fullerenos
 El cantilever será de Si3N4 de punta triangular
con constante de muelle de 0.02 N/m.
 Ejerceremos una fuerza de 0.1 nN sobre la
muestra, apoyada en un sustrato de HOPG.
 Utilizaremos los métodos de altura y fuerza
constante.
 Se rotará la muestra para eliminar posibles
artefactos.

37. Solitones en fullerenos
 En la dirección (0001) se observan las
superredes onduladas de dimensión
molecular.
 Cada capa muestra dos tipos de
empaquetamiento diferentes.
 Aparecen placas en la imagen. Esto
sugiere más crecimiento. Las placas se
desgastan cada vez que pasa la punta.

38. Solitones en fullerenos

39. Solitones en fullerenos
 Dejando la muestra en un sitio oscuro y
seco durante dos semanas aparecerán
terrazas en ciertas direcciones, aunque se
sigue conservando la estructura de
superred.
 Amplificando la imagen y aplicando un
filtro pasa-baja de 1 kHz se puede
analizar la estructura, cuyo carácter
periódico se confirma con una
transformada de Fourier.

40. Solitones en fullerenos

41. Solitones en fullerenos
 Todo esto nos ayuda a identificar la
estructura cristalina del fullereno, que será
hcp con incrustaciones de fcc.

42. Efectos de la corrosión
 Mediante sputtering por magnetrón DC se
depositan capas de diferentes espesores
de TiN y NbN sobre acero de
herramientas.
 Con AFM se puede estudiar la corrosión
de las muestras tratadas y sin tratar.
 El acero cambia su rugosidad de 4.6 a
266 nm, mientras que la superred varía de
5.2 a 5.4 nm.

43. Efectos de la corrosión

44. Efectos del orden espontáneo
 Las superredes dependen sensiblemente
de la deposición de los materiales.
 En capas de AlGaN, donde se varía el
flujo de deposición (técnica de epitaxia
metal-orgánica en fase vapor) pueden
aparecer espontáneamente agregados.
 Con AFM se puede determinar al observar
la superficie qué condiciones son las
idóneas.

45. Efectos del orden espontáneo

46. Efectos del orden espontáneo
 Con cortes transversales podemos
estudiar las superredes. Para ello se pule
la zona cortada y se trata químicamente
para que revele su estructura, la cual
presentará máximos y mínimos de
concentración de aluminio, debido a la
rápida desorción del galio.

47. Efectos del orden espontáneo

48. Películas delgadas de óxido de perovskita
 Sobre SrTiO3 se deposita BaTiO3 mediante
MBE con láser.
 Mediante AFM conoceremos su
topografía.

49. Caracterización de antipuntos
 Sobre un sustrato de dióxido de silicio se
depositan capas de plomo y germanio
mediante MBE.
 Con técnicas litográficas se realizan
ciertos agujeros en la superred.
 Como el Ge es aislante, no podemos
utilizar STM, luego recurriremos a AFM en
modo Tapping.

50. Caracterización de antipuntos
 AFM indica el espaciado entre antipuntos,
además de su profundidad. También
muestra que las esquinas están
redondeadas.
 Por el tamaño de la punta se producen
efectos de convolución al estudiar las
paredes.
 La zona llana de la muestra presenta una
rugosidad de 1nm.

51. Caracterización de antipuntos

52. Propiedades de fractura
 Con MBE se crean superredes de GaAs/AlAs.
 Al fracturar la superred con AFM podemos ver
que aparecen crestas en las capas de AlAs
debido a la deformación plástica.
 No se puede determinar la profundidad entre
capas contiguas por los efectos de la
convolución entre la forma de la punta y la
topografía, por lo que sólo se podrá conocer el
espesor de las capas que forman las crestas.

53. Propiedades de fractura

54. Superred de CoO/Co
 Interesan por sus propiedades
magnéticas: el CoO es antiferromagnético
y el Co es ferromagnético.
 Se aplican para mecanismos de rotación y
para memorias RAM.
 Se depositan mediante MBE sobre un
sustrato de GaAS (111) con una capa de
oro.

55. Superred de CoO/Co
 Con AFM se determina que el sustrato
presenta escalones atómicos en la
dirección [0-11].

56. Superred de CoO/Co
 Elóxido de cobalto presenta una
rugosidad cuadrática media de 0.6 nm
tras un proceso de irradiación.

57. Puntos cuánticos en superredes
 Cuando se supera un cierto límite de
deposición de manera espontánea, el
compuesto se agrupa en islas, las cuales
presentarán un confinamiento cuántico.
 Las islas inducirán campos de esfuerzos
sobre las capas intermedias.
 Mediante la técnica CVD se deposita Ge
sobre Si (001).

58. Puntos cuánticos en superredes
 Con AFM en modo contacto podremos
conocer las dimensiones de los puntos
dependiendo del espesor de la capa de
silicio de recubrimiento.

59. Puntos cuánticos en superredes

60. Comparación de STM y AFM
 Se crea mediante CVD metal-orgánico
una superred de GaAs/AlGaAs.
 Posee aplicación en dispositivos
optoelectrónicos.
 Tras un corte transversal se puede
determinar la estructura de superred.

61. Comparación de STM y AFM

62. Comparación de STM y AFM
 AFMtambién nos permite la creación de
imágenes de fuerza elástica y lateral.

63. Comparación de STM y AFM
 Sepuede aplicar una transformada de
Fourier para verificar la estructura de la
superred.