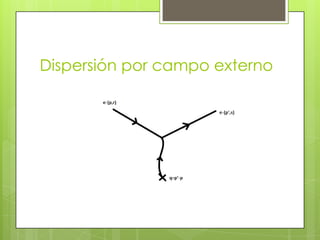
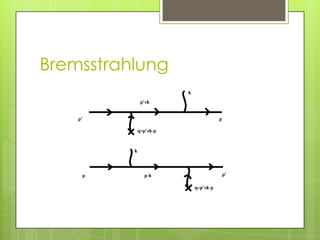
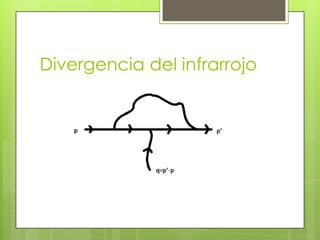
Este documento resume varios procesos de baja orden en la electrodinámica cuántica (QED), incluyendo la dispersión de un electrón por un campo externo estático, el bremsstrahlung (radiación de frenado producida cuando un electrón es desviado por un núcleo), y la divergencia del infrarrojo que ocurre en ciertos cálculos. También introduce conceptos como los operadores de creación y destrucción de fotones y las reglas de Feynman para calcular probabilidades de transición.

1. Procesos QED
de bajo orden
Javier García Molleja

2. Introducción
 En la Teoría Cuántica de Campos se
considera únicamente el estado inicial y
final del fotón, no el trayecto o
probabilidad intermedia, que se
considera un proceso virtual.
 Se utiliza por simplicidad la notación de
Dirac.

3. Introducción
 El primer factor son las matrices del
campo de Dirac.
 El segundo factor es el cuadrivector.
 Analicemos entonces los procesos de
bajo orden de la Electrodinámica
Cuántica (QED).

4. Dispersión por campo externo
 El campo electromagnético cuantizado
se estudia mediante operadores de
creación y destrucción.
 Solo es aplicable la descripción clásica si
no se dan fluctuaciones.

5. Dispersión por campo externo
 Veamos la dispersión de un electrón
originado por un campo estático.

6. Dispersión por campo externo
 Es necesario evaluar el elemento de
matriz de la anterior expresión.

7. Dispersión por campo externo
 Se ignora la delta de Dirac para el
momento.
 La conservación de la energía queda
indicada por el uso de las deltas de Dirac.
 Este resultado es generalizable y se
pueden aplicar las reglas de Feynman.

8. Dispersión por campo externo

9. Dispersión por campo externo
 La sección eficaz se puede obtener.
 Veamos la probabilidad de transición.

10. Dispersión por campo externo
 El valor T es finito, pero muy largo.
 Este valor w se puede multiplicar por la
densidad de estados finales y dividirse por
el flujo de electrones.

11. Dispersión por campo externo
 Se dará la dispersión de Mott si el núcleo
es muy masivo y solo interacciona
coulombianamente.
 Además, dicho núcleo se trata como una
carga puntual.

12. Dispersión de campo externo
 A velocidades relativistas se considera
que hay una dependencia con el espín.

13. Bremsstrahlung
 La deflexión del electrón por un núcleo
provoca la emisión de radiación por
parte de este y su consecuente frenado.
 Dicha radiación es denominada la
radiación de frenado.
 El bremsstrahlung es un fenómeno
importante cuando los electrones
atraviesan la materia.

14. Bremsstrahlung

15. Bremsstrahlung
 El campo de Coulomb está también
cuantizado.
 Aunque se emita radiación se conserva el
momento y la energía.

16. Bremsstrahlung
 La sección eficaz entonces se define
como:

17. Bremsstrahlung
 Si a la anterior expresión la promediamos
en el espín se obtiene la sección eficaz
de Bethe-Heitler para el bremsstrahlung
de Coulomb.
 En el caso de electrones débiles se tiene
que ~0, por lo que la fórmula queda
como:

18. Bremsstrahlung
 Existen singularidades en el infrarrojo, es
decir, cuando tiende a 0.
 En estas condiciones los diagramas de
Feynman tienen, para el electrón, un
cuadrimomento real y los propagadores
divergen.

19. Divergencia del infrarrojo
 Bajo ciertas condiciones un fotón puede
tener muy poca energía, por lo que se hace
probable que el aparato de detección no lo
identifique.
 Otras veces puede pasar que no se está
seguro si el fotón proviene de una colisión
elástica o de una inelástica.
 En este caso se puede asumir que su sección
eficaz es la suma del bremsstrahlung elástico
y del inelástico.

20. Divergencia del infrarrojo
 Uno de los integrandos en este caso
diverge al ser proporcional a -1.
 Este fenómeno se conoce como
catástrofe del infrarrojo.
 Dicha catástrofe se puede eliminar
dando ficticiamente masa no nula al
fotón y después tomar límites.

21. Divergencia del infrarrojo
 Se tiene que es la masa del fotón.
 Dichos fotones pueden estar polarizados
longitudinal y transversalmente.
 Este planteamiento necesita de la
introducción de correcciones.

22. Divergencia del infrarrojo

23. Divergencia del infrarrojo
 Todo esto da que:

24. Divergencia del infrarrojo
 Si tiende a 0 se tiene en el límite que
B( ) tiende a ∞ y que R( ) tiende a -∞. Es
decir, las singularidades se cancelan.
 Estas son las denominadas correcciones
radiativas.
 Esta técnica influye en la sección eficaz
experimental, por lo que las correcciones
se aplican a lo medido.

25. Divergencia del infrarrojo
 La catástrofe se origina por tratar en la
teoría de perturbaciones al
bremsstrahlung y a la dispersión elástica
como procesos separados.
 Las correcciones a mayor orden dan una
cancelación exacta del orden , es la
llamada teoría de Bloch-Nordsieck.
 Por consiguiente, si hay dispersión elástica
hay obligatoriamente bremsstrahlung.