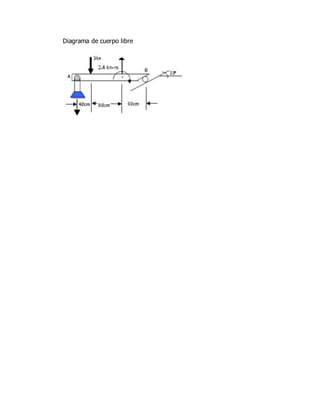
Este documento contiene tres problemas de ingeniería resueltos. El primer problema determina las reacciones en un apoyo fijo dado las tensiones en un alambre. El segundo problema calcula la tensión en un cable y la reacción en una articulación que sostiene una caja con una grúa. El tercer problema determina las reacciones en los apoyos de una viga usando ecuaciones de equilibrio.

1. UNIVERSIDAD FERMIN TORO
VICERRECTORADO ACADEMICO
FACULTAD DE INGENIERIA
ACTIVIDAD N°04
Autor: Alvimar Vargas: 23849955

2. Cabudare, 2015
1).- Si la TENSION en el ALAMBRE BD es de 350 Lb, a) Determine las
REACCCIONES en el APOYO fijo C de la Figura que se muestra a continuación. B)
Haga D.C.L. (Nota: Σ Fuerzas y Σ Momento)
Solución
ℎ = √10𝑖𝑛2 + 24𝑖𝑛2 = 26 𝑖𝑛
𝐶𝑜𝑠 =
10
26
𝑆𝑒𝑛 =
24
26
𝑇𝐵𝐷 = 350 𝑙𝑏
Aplicando la condición de equilibrio tenemos
∑ 𝑀𝐶 = 0 ;
𝑀𝑐 + 180 𝑙𝑏 𝑥 20 𝑖𝑛 + 350 𝑙𝑏 𝑥
10 𝑖𝑛
26 𝑖𝑛
𝑥 24 𝑖𝑛 − 350 𝑥
24 𝑖𝑛
26 𝑖𝑛
𝑥 6 𝑖𝑛 + 100 𝑙𝑏 𝑥 16 𝑖𝑛 = 0

3. 𝑀𝑐 + 3600 𝑙𝑏 𝑥 𝑖𝑛 − 3230,76 𝑙𝑏 𝑥 𝑖𝑛 − 1938,46 + 1600 𝑙𝑏 𝑥 𝑖𝑛
𝑀𝑐 + 30.77 𝑙𝑏 𝑥 𝑖𝑛 = 0
𝑀𝑐 = −30, 77 𝑙𝑏 𝑥 𝑖𝑛
𝑀𝑐 = −30,77 𝑙𝑏 𝑥 𝑖𝑛
∑ 𝐹𝑥 = 0; 𝐶𝑥 − 100 𝑙𝑏 350 𝑙𝑏 𝑥
10 𝑖𝑛
26 𝑖𝑛
= 0
𝐶𝑥 + 34.26 𝑙𝑏 = 0
𝐶𝑥 = −34, 62 𝑙𝑏
𝐶𝑥 = 34,62 𝑙𝑏
∑ 𝐹𝑦 = 0 ;
𝐶𝑦 − 180 𝑙𝑏 − 350 𝑙𝑏 𝑥
24 𝑖𝑛
26 𝑖𝑛
= 0
𝐶𝑦 − 503, 08 𝑙𝑏 = 0
𝐶𝑦 = 503,08 𝑙𝑏

4. 2).- Una caja de 200 Lb se sostiene mediante la grúa Viajera mostrada a
continuación si a = 2,0 ft. Determine: a) Dibuje Diagrama de Cuerpo Libre (D. C.L.) b)
La tensión en el Cable CD, c) La reacción en la Articulación B
Diagrama del cuerpo libre
Solución

5. Aislamos el cuerpo en estudio y seguimos con colocar todas las fuerzas externas
que actúan con sus dimensiones, luego aplicamos la condición de equilibrio
+ ∑ 𝐹𝑥 = 0 ; 𝐵𝑥 + 𝑇𝐶𝐷 𝑥 Cos(35°) = 0 (𝐼)
+ ∑ 𝐹𝑦 = 0 ; 𝐵𝑦 + 𝑇𝐶𝐷 𝑆𝑒𝑛 (35°) - 200 lb = 0 (II)
+ ∑ 𝑀𝐵 = 0
200 𝑙𝑏 𝑥 2,0 𝑓𝑡 − 𝑇𝐶𝐷 𝑥 𝐶𝑜𝑠 (35°) 𝑥 0.5 𝑓𝑡 − 𝑇𝐶𝐷 𝑥 𝑆𝑒𝑛 (35°) 𝑥 𝐶𝐵 = 0 (𝐼𝐼𝐼)
Tenemos que:
𝑡𝑎𝑛𝑔 (55°) =
𝐶𝐵
1.5 𝑓𝑡
𝐶𝐵 = 1.5 𝑓𝑡 𝑥 𝑡𝑎𝑛𝑔 (55°)
Sustituimos CB en (III) y tenemos que:
400 𝑙𝑏 𝑥 𝑓𝑡 − 𝑇𝐶𝐷 𝑥 𝐶𝑜𝑠 (35°) 𝑥 0.5 𝑓𝑡𝑇𝐶𝐷 𝑥 𝑆𝑒𝑛 (35°) 𝑥 1,5 𝑓𝑡 𝑥 𝑡𝑎𝑛𝑔 (55°) = 0
+ ∑ 𝑀𝐵 = 0
400 𝑙𝑏 𝑥 𝑓𝑡 − 1,64 𝑓𝑡 𝑥 𝑇𝐶𝐷 = 0
𝑇𝐶𝐷 =
400 𝑙𝑏 𝑥 𝑓𝑡
1,64 𝑓𝑡
= 243,90 𝑙𝑏
𝑇𝐶𝐷 = 243,90 𝑙𝑏
Calculamos las reacciones 𝐵𝑥 y 𝐵𝑦, sustituiomos el calor de 𝑇𝐶𝐷 (𝐼) y (𝐼𝐼) tenemos
que:
En (𝐼)
𝐵𝑥 + 243,90 𝑙𝑏 𝑥 𝐶𝑜𝑠 (35°) = 0
𝐵𝑥 + 199,80 𝑙𝑏 = 0
𝐵𝑥 = −199, 80 𝑙𝑏
𝐵𝑥 = 199,80 𝑙𝑏

6. En (𝐼𝐼)
𝐵𝑦 + 243, 90 𝑙𝑏 𝑥 𝑆𝑒𝑛 (35°)− 200 𝑙𝑏 = 0
𝐵𝑦 − 61,10 𝑙𝑏 = 0
𝐵𝑦 = 61,10 𝑙𝑏

7. 3).- a) Dibuje el Diagrama de Cuerpo libre (D.C.L.) de la Viga AB
b) Determine las reacciones en los apoyos A y B
Nota: Usando Ecuaciones de Equilibrio
Solución
40 𝑐𝑚 𝑥
1 𝑚
100 𝑐𝑚
= 0,40 𝑚
80 𝑐𝑚 𝑥
1 𝑚
100 𝑐𝑚
= 0,80 𝑚
60 𝑐𝑚 𝑥
1 𝑚
100 𝑐𝑚
= 0,60 𝑚
Ecuaciones de equilibrio
∑ 𝐹𝑥 = 0 𝐴𝑥 − 𝐵𝑥 = 0
Tenemos que 𝐵𝑥 = 𝐵 𝑥 𝑆𝑒𝑛 (30°)
Entonces 𝐴𝑥 − 𝐵 𝑥 𝑆𝑒𝑛 (30°) = 0 (𝐼)
∑ 𝐹𝑦 = 0 𝐴𝑦 − 2𝑘𝑛 + 𝐵𝑦 = 0
Pero tenemos que 𝐵𝑦 = 𝐵 𝑥 𝐶𝑜𝑠 (30°)
Entonces 𝐴𝑦 − 2 𝑘𝑛 + 𝐵 𝑥 𝐶𝑜𝑠 (30°) = 0 (𝐼𝐼)
A
B
80cm 60cm40cm
30°
2kn
·
2.4 kn-m

8. Como en 𝐴 tenemos una articulación, hay dos componentes que restringe el
movimiento y tenemos dos ecuaciones y 3 incógnitas sabiendo que los momentos en las
articulaciones son cero, nos apoyamos en una tercera ecuaciones
+ ∑ 𝑀𝐴 = 0
+ ∑ 𝑀𝐴 = 0
− 2𝑘𝑛 ( 0,40) − 1,4 𝑘𝑛 𝑥 𝑚 + 𝐵𝑥 𝐶𝑜𝑠 (30°) 𝑥 1,80𝑚 = 0
−0,80 𝑘𝑛 𝑥 𝑚 − 2,4 𝑘𝑛 𝑥 𝑚 + 𝐵 𝑥 Cos(30°) 𝑥 1,80 𝑚 = 0
−3,20 𝑘𝑛 𝑥 𝑚 + 𝐵 𝑥 𝐶𝑜𝑠 (30°) 𝑥 1,80 𝑚 = 0
𝐵 =
320 𝑘𝑛 𝑥 𝑚
𝐶𝑜𝑠 (30°) 𝑥 1,80𝑚
𝐵 = 2.05 𝑘𝑛
Sustituyendo el valor de B en (𝐼) y ( 𝐼𝐼)
( 𝐼) 𝐴𝑥 − 2,50 𝑘𝑛 𝑥 𝑆𝑒𝑛 (30°) = 0
𝐴𝑥 = 2,05𝑘𝑛 𝑥 𝑆𝑒𝑛 (30°) = 1,03 𝑘𝑛
𝐴𝑥 = 1,03 𝑘𝑛
( 𝐼𝐼) 𝐴𝑦 − 2𝑘𝑛 + 2,05 𝑘𝑛 𝑥 𝐶𝑜𝑠 (30°) = 0
𝐴𝑦 = 2 𝑘𝑛 − 2,05 𝑘𝑛 𝑥 𝐶𝑜𝑠 (30°) = 0,22 𝑘𝑛
𝐴𝑦 = 0,22 𝑘𝑛
𝐴𝑥 = 1,03 𝑘𝑛 , 𝐴𝑦 = 0,22 𝑘𝑛 , 𝐵 = 2,05𝑘𝑛

9. Diagrama de cuerpo libre