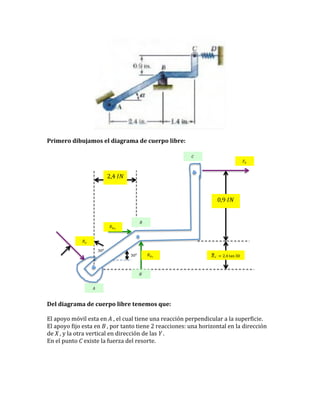
(a) Se dibuja el diagrama de cuerpo libre de la palanca BCD con apoyos en B y C. (b) Aplicando las ecuaciones de equilibrio, se determinan las reacciones en los apoyos B y C como RBy = 10.74 lb, RBx = 2.60 lb, y RC = 449 N. (c) Usando la fuerza en el resorte Fs = 9.24 lb, se calcula la constante del resorte K = 7.7 lb/in.

1.
Primero
dibujamos
el
diagrama
de
cuerpo
libre:
!!
!! !
2,4!!"!
0,9!!"!
!!
!! ! !
!! !
30! !
!! ! !
30! !
!! ´ = 2,4 tan 30!
!´ !
!!
Del
diagrama
de
cuerpo
libre
tenemos
que:
El
apoyo
móvil
esta
en
A
,
el
cual
tiene
una
reacción
perpendicular
a
la
superficie.
El
apoyo
fijo
esta
en
B
,
por
tanto
tiene
2
reacciones:
una
horizontal
en
la
dirección
de
X
,
y
la
otra
vertical
en
dirección
de
las
Y
.
En
el
punto
C
existe
la
fuerza
del
resorte.

2. -Body Diagram:
e-Body Diagram:
(a) From free-body diagram of lever BCD
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ((50 mm ) − 200 N ( 75 mm ) = 0
ΣM C = 0: TAB 50 mm −
AB = 300
Ahora
aplicando
las
ecuaciones
de
equilibrio
tenemos:
∴ TAB = 300
(b) From free-body diagram of lever BCD
(b) From free-body diagram of lever BCD
olutions Manual Organization System
19.
ΣFxx = 0: 0: 𝑅Cxsin0.6 ( 300 N ) = 0 𝐹 = 0 (𝐼)
ΣF 𝐹 0: 200 N + C x + 30 + 𝑅! + !
= = 200 N + ! +
!
!
∴ C xx = −380 N
or
C x = 380 N
∴ C = −380 N
or
C x = 380 N
ΣFyy = 0: C yy + 0.8 ( 300 N ) = 0
ΣF = 0: C + 0.8 300 N = 0
𝐹! = 0: − 𝑅! cos 30 + 𝑅!! = 0 (𝐼𝐼)
∴ C = −240 N
∴C
(a) From free-body diagram of lever BCD yy = −240 N
or
or
C y = 240 N
C y = 240 N
2
2
ΣM C Then TAB ( 50 mm )C x2200 y2 (= mm ))2 + ( 240 )2 = 449.44 N
= 0:
C = C2 + C N = ( 380 = + 240 2 = 449.44 N
C = −x + C y 75 380 0
Then
𝑀! = 0: 𝑅! sin 30 2,4 tan 30 + 𝑅! cos 30 2,4 − 𝐹! 0,9 = 0 (𝐼𝐼𝐼)
∴T
= 300
AB
⎛ Cy ⎞
C ⎞
⎛ − 240 ⎞
1
⎞
⎛
and
θ = tan −−1⎜⎛ y ⎟ = tan −−11⎜ − 240 ⎟ = 32.276°
⎟
and
θ lever BCD ⎟ = tan ⎜
= tan ⎜⎜
⎟ = 32.276°
(b) From free-body diagram of
⎟
⎝ − 380 ⎠
⎝⎜C xx ⎠
⎝ − 380 ⎠
⎝C ⎠
𝐶𝑜𝑚𝑜 𝑅! N ) = 0
ΣFx = 0: 200 N + Cx + 0.6 ( 300= 3 𝑙𝑏 𝑠𝑒𝑔𝑢𝑛 𝑒𝑙 𝑒𝑛𝑢𝑛𝑐𝑖𝑎𝑑𝑜
32.3° ▹
or C = 449 N
32.3° ▹
or C = 449 N
∴ C x = −380 N
or
C x = 380 N
De
(III)
se
tiene
que:
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
3 sin 30 2,4 tan 30 = 240 N cos 30 2,4 = 𝐹! 0,9
+ 3
∴ C y = −240 N
or
Cy
2
2
2
2
sin 30 240 tan 449.44 3
C = C x + C y =3 ( 380 ) + ( 2,4 ) = 30 + N cos 30 2,4 = 9,24 𝑙𝑏
Then
𝐹! =
0,9
⎛ Cy ⎞
−1
−1 ⎛ − 240 ⎞
and
θ = tan ⎜ ⎟ = tan ⎜
⎟ = 32.276°
⎜C ⎟
Ahora
se
determina
la
c− 380 ⎠
⎝ onstante
K
,
mediante
la
fuerza
en
el
resorte:
⎝ x⎠
or C = 449 N
32.3° ▹
𝐹! = 𝜒𝜅
𝐹!
9,24
𝜅=
=
= 7,7 𝑙𝑏 𝑖𝑛
𝜒
1,2
Ahora
para
la
reacción
en
B
tenemos:
De
(I)
se
tiene
que:
𝑅!! = −𝑅! sin 30 − 𝐹! = −3 sin 30 − 9,24 = 10,74 𝑙𝑏 𝑜 𝑅!! = 10,74 𝑙𝑏 ←
De
(II)
se
tiene
que:
Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinandcos 30 E.Russell cos 30 Jr., 2,60 𝑙𝑏 𝑜 𝑅! = 2,60 𝑙𝑏 ↑
𝑅 8/e, Ferdinand P. Beer, Russell Johnston, =
Mechanics for Engineers: Statics and Dynamics,!! = 𝑅! P. Beer, E. = 3 Johnston, Jr.,
!
Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
R. Eisenberg, William E. Clausen, David Mazurek,Phillip J. Cornwell
The McGraw-Hill Companies.
7 The McGraw-Hill Companies.
𝑃𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜: 𝑅! =
s: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
𝑅!! ! + 𝑅!! ! =
10,74
!
+ 2,60
!
= 11,05 𝑙𝑏