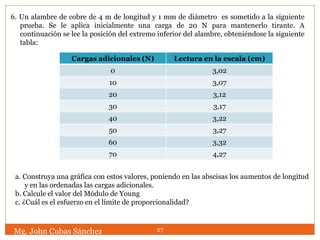
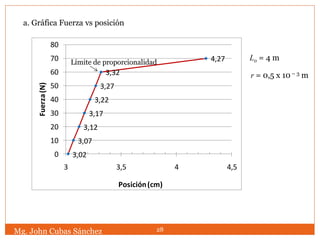
El documento trata sobre la elasticidad y los diferentes tipos de esfuerzos y deformaciones que pueden producirse en un cuerpo deformable. Explica conceptos como el módulo de Young, el coeficiente de Poisson, los límites de elasticidad y ruptura, y las relaciones entre los distintos módulos elásticos. También incluye ejemplos numéricos para ilustrar el cálculo de esfuerzos, deformaciones y módulos a partir de datos experimentales.

2. Mg. John Cubas Sánchez 2
1. Al finalizar la unidad el estudiante estará capacitado para analizar
los diferentes tipos de esfuerzos y su correspondientes
deformaciones producidas en cuerpos deformables.
2. Al finalizar la unidad el estudiante estará capacitado para utilizar
los diferentes módulos elásticos característicos de los materiales
para modelar comportamientos elásticos y plásticos de los
mismos.

3. Mg. John Cubas Sánchez 3
ELASTICIDAD
Parte de la Física
que estudia las
Leyes que
gobiernan las
DEFORMACIONES
sufridas por un
cuerpo cuando se le
aplica un
ESFUERZO externo.
Todo cuerpo sobre
el que actúan
esfuerzos externos
sufre una
deformación que
depende de la
naturaleza del
sólido y de las
fuerzas que sobre él
actúan.

4. Mg. John Cubas Sánchez 4
Esfuerzo por tracción y compresión:
Consideremos un cuerpo al que se le aplican dos fuerzas
exteriores iguales paralelas en sentido contrario y
perpendiculares a dos secciones
Si F>0 (hacia fuera del cuerpo) fuerza de
tracción
Si F<0 (hacia dentro del cuerpo) fuerza de
compresión
F F F F

5. Mg. John Cubas Sánchez 5
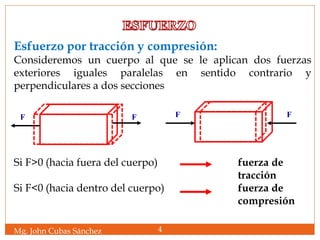
Se define el esfuerzo tensor y compresor “e ” como el
cociente entre la fuerza (de tensión o compresión)
aplicada perpendicularmente al área de la sección
transversal sobre la que se aplica y dicha área.
El resultado será un cambio en la longitud el mismo.
Si Lo es la longitud original del cuerpo y L su longitud
después de aplicar el esfuerzo, el alargamiento o
elongación producido será ΔL = L - Lo
A
F
e [N/m2 = Pa]
si ΔL>0 L>Lo fuerza de tracción
si ΔL<0 L<Lo fuerza de compresión

6. La deformación producida dependerá de la tensión o
compresión por unidad de área transversal sobre la que se
aplica la fuerza (esfuerzo tensor o compresor).
Si el esfuerzo aplicado sobre el cuerpo no es demasiado
grande (reversible), experimentalmente se encuentra que el
esfuerzo aplicado es directamente proporcional a la
deformación producida:
Mg. John Cubas Sánchez 6
OL
L


e
Y
[adimensional]
[N/m2 = Pa]
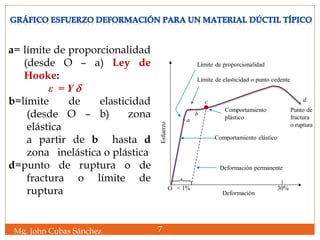
Y = módulo de Young, es
una propiedad
característica del material
Deformación longitudinal ():
Es el cociente entre la variación de longitud
producida y la longitud inicial del cuerpo.

7. a= límite de proporcionalidad
(desde O – a) Ley de
Hooke:
ε = Y 
b=límite de elasticidad
(desde O – b) zona
elástica
a partir de b hasta d
zona inelástica o plástica
d=punto de ruptura o de
fractura o límite de
ruptura
Mg. John Cubas Sánchez 7
Deformación
Esfuerzo
a
Límite de proporcionalidad
b
Límite de elasticidad o punto cedente
d
Punto de
fractura
o ruptura
c
Comportamiento
plástico
Comportamiento elástico
< 1% 30%
Deformación permanente
O

8. Mg. John Cubas Sánchez 8

9. Límite de
proporcionalidad:
es el valor máximo del esfuerzo
que el sólido puede soportar para
que el esfuerzo aplicado y la
deformación producida sean
proporcionales (zona: ley de
Hooke)
Límite elástico o
límite de
elasticidad
es el valor máximo de las fuerzas
exteriores por unidad de área (o
esfuerzo) que el sólido puede
soportar comportándose como
elástico. A partir de dicho valor las
deformaciones son permanentes y
el cuerpo se comporta como
inelástico o plástico.
Mg. John Cubas Sánchez 9

10. Límite de
ruptura o
esfuerzo de
ruptura:
es la mínima fuerza
por unidad de
sección (esfuerzo)
capaz de producir la
ruptura del cuerpo.
Mg. John Cubas Sánchez 10
Todo cuerpo posee
intervalos de
esfuerzos donde se
comporta como
elástico e intervalos
de esfuerzos mayores
donde se comporta
como inelástico.

11. S < 1 el cuerpo no se rompe
S ≥ 1 el cuerpo se rompe
Mg. John Cubas Sánchez 11
C
S
e
e

Coeficiente de
seguridad:
es el cociente entre
la fuerza máxima por
unidad de sección
(esfuerzo aplicado) y
el esfuerzo de
ruptura (eC).
[adimensional]

12. Un aumento o disminución de la longitud de un cuerpo
por la aplicación de un esfuerzo tensor o compresor
respectivamente, produce una variación en el área
transversal donde se aplica el esfuerzo.
Si Ao es el área transversal del cuerpo antes de aplicar
el esfuerzo y A el área posterior a la aplicación del
esfuerzo.
A<Ao un esfuerzo de tracción
A>Ao un esfuerzo de compresión
Mg. John Cubas Sánchez 12
Ao
A
Lo
L
F FF F
Deformación lateral ():

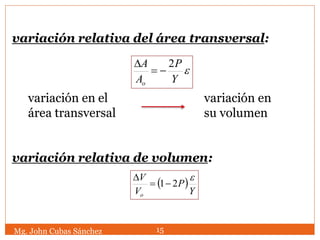
13. Despejando la deformación lateral:
Recordando la ley de Hooke:
Lo
wo
Ao
Mg. John Cubas Sánchez 13
Ow
w





P
P = Coeficiente de Poisson
e Y
 P
si L > Lo w < wo
si L < Lo w > wo
 e
P
Y
L
w
A
un esfuerzo de tracción
un esfuerzo de compresión
[adimensional] [adimensional]
La deformación lateral
Obtenemos:
P >0

14. - El signo negativo indica la disminución de las dimensiones
laterales (w < wo) cuando aumenta la longitud del cuerpo
(L>Lo).
- Tanto el módulo de Young (Y ) como el de Poisson (P)
dependen de la naturaleza del material con que está hecho el
cuerpo.
Mg. John Cubas Sánchez 14

oA
A
P


2
1Se puede obtener del coeficiente de Poisson:

15. variación relativa del área transversal:
variación en el variación en
área transversal su volumen
variación relativa de volumen:
Mg. John Cubas Sánchez 15
e
Y
P
A
A
o
2


 
Y
P
V
V
o
e
21


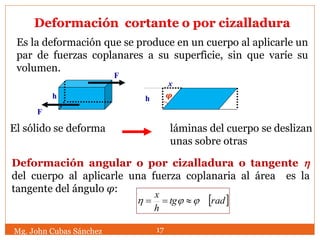
16. Disminución del volumen de un cuerpo al aplicarle un esfuerzo
de compresión igual en todas sus caras (presión).
Variación relativa de volumen o
deformación volumétrica:
Mg. John Cubas Sánchez 16
O
V
V
V

V
p
V
p
B O
V 





1 1
O
V
B V p


  

 PBY 213 
Deformación volumétrica
Vo V
B módulo de compresibilidad N/m2 = Pa
 coeficiente de compresibilidad m2/N = Pa – 1
El módulo de compresibilidad está relacionado con
el módulo de Young y el coeficiente de Poisson:
Al relacionar el incremento de presión con la
deformación volumétrica obtenemos:
[adimensional]

17. El sólido se deforma láminas del cuerpo se deslizan
unas sobre otras
Mg. John Cubas Sánchez 17
x
φh
 radtg
h
x
 
Deformación cortante o por cizalladura
F
h
F
Es la deformación que se produce en un cuerpo al aplicarle un
par de fuerzas coplanares a su superficie, sin que varíe su
volumen.
Deformación angular o por cizalladura o tangente 
del cuerpo al aplicarle una fuerza coplanaria al área es la
tangente del ángulo φ:

18. Si el esfuerzo cortante no es demasiado
grande ambas cantidades están
relacionadas linealmente e ~ 
Mg. John Cubas Sánchez 18
A
F//
e

e//
G
 P
Y
G


12
El módulo de cizalladura (G) estará relacionado
con los módulos de Young y de Poisson:
En este caso la fuerza F aplicada al sólido produce
un esfuerzo cortante o esfuerzo de
cizalladura:
G módulo de deslizamiento, módulo de cizalladura,
módulo de torsión o coeficiente de rigidez
(combinación de esfuerzos de tracción y de compresión)
[N/m2 = Pa]

19. Esfuerzo Deformación
Módulos de
elasticidad
Tensor Longitudinal
Módulo de
Young
Compresor Lateral
Coeficiente
de Poisson
Cortante Cizallante
Módulo de
Torsión
Presión Volumétrica
Módulo de
compresibilidad
Coeficiente de
compresibilidad
A
Fe
A
Fe
A
F//e
A
F
p 
oL
L

ow
w



  tg
h
x
o
V
V
V

LA
LF
Y o



e
L
L
P
o
o


 
w
w



e
TgA
F
xA
hF
G 
dV
dp
V
V
p
VB oo 



B
1

Mg. John Cubas Sánchez 19

20. Mg. John Cubas Sánchez 20
 PBY 213 
 P
Y
G


12
Relación entre
módulos elásticos:
Nombre Fórmula
Coeficiente de seguridad
Esfuerzo tensor o
compresor
Coeficiente de Poisson
Deformación unitaria del
área
Deformación volumétrica
C
S
e
e

  e
P
Y

oA
A
P


2
1
Y
P
A
A
o


 e
2
 
Y
P
V
V
o


 e
21 e Y
Ley de Hooke:

21. Mg. John Cubas Sánchez 21

22. 500 kg
F =mg =4900 N
Lo = 3 m
A = 2 x 10-5 m2
L = 4 x10-3 m
Esfuerzo:
A
Fe
5
102
4900


x
e
e = 2,45 x 108 Pa
Deformación:
oL
L

3
104 3

x

 = 1,33 x 10 -3

e
Y
Módulo de Young:
3
8
1033,1
1045,2


x
x
Y
Y = 1,84 x 10 11 Pa
Mg. John Cubas Sánchez 22
1. En un experimento para medir el Módulo de Young, una carga de 500 Kg suspendida de un
alambre de 3 m de longitud y 0,20 cm2 de sección recta produjo un alargamiento en el
mismo de 0,4 cm respecto a su longitud antes de haber sido cargado. ¿Cuál es el esfuerzo,
la deformación y el valor del módulo de Young para este alambre?

23. A = 1 x 5 x10 -3
A = 5 x10 - 3 m2
x = 2 x 10 - 4 m
G = 0,36 x 10 11 Pa
xA
hF
G 
h = 1 m
h
AGx
F 
1
1036,0105102 1134
xxxxx
F


F = 36 000 N
Mg. John Cubas Sánchez 23

e//
G
h
x
A
F
G 
2. Supóngase que el objeto de la figura es una lámina de
bronce cuadrada de 1 m de lado y 0,5 cm de espesor,
¿qué fuerza F ha de ejercerse? si el desplazamiento x
de la figura es 0,02 cm. El coeficiente de rigidez del
bronce es 0,36 x 10 11 Pa
1 m
0,5 cm
1 m
fh
x A
F
F

24. Vo = 0,2 m3
 p = 2,04 x 107 Pa
 = 20 x 10-6 atm -1
B
1


1
B
6
1020
1


x
B atm
atm
Pax
atmxB
1
10013,1
.105
5
4

B = 5,065 x 109 Pa
V
p
VB o



B
p
VV o


9
7
10065,5
1004,2
2,0
x
x
V 
 V = - 8,06 x 10 – 4 m3
Mg. John Cubas Sánchez 24
3. El volumen de aceite contenido en una prensa hidráulica es de 0,2 m3. Calcule la
disminución de volumen de aceite cuando está sometido a una presión de 2,04 x 10 7 Pa. El
coeficiente de compresibilidad del aceite es de 20 x 10 – 6 atm – 1.

25. Lo = 4 m
A= 5 x 10 – 5 m2
 L= 2 x 10 – 3 m
F = 12 000 N
LA
LF
Y o


35
102105
412000


xxx
x
Y
Y = 4,8 x 10 11 Pa
Mg. John Cubas Sánchez 25

e
Y
oL
L
A
F
Y


4. Una varilla de acero de 4 m de longitud y 0,5 cm2 de sección, se estira 0,2 cm bajo la
acción de una tensión de 12 000 N. ¿Cuál es el módulo de Young para este acero?

26. Lo = 50 m
A= 6,36 x 10 – 5 m2
 L= 1,5 m
F = 80 x 9,8 N = 784 N
do = 9 x 10 – 3 m
4
2
od
A 
 
4
109 23

x
A 
Módulo de Young:
5,11036,6
50784
5
xx
x
Y 

Y = 4,1 x 10 8 Pa
Ld
Ld
P
o
o



Coeficiente de Poisson:
o
o
L
LPd
d


50
5,11092,0 3
xxx
d


 d = 54 x 10 – 6 m
Mg. John Cubas Sánchez 26
m = 80 kg
LA
LF
Y o


F
Lo = 50 m
L
do
P = 0,2
5. Una cuerda de nailon de las utilizadas por los montañistas se alarga 1,5 cm bajo la acción de un escalador
de 80 kg. Si la cuerda tiene 50 m de longitud y 9 mm de diámetro, ¿cuál es el módulo de Young para este
material? Si el coeficiente de Poisson para el nailon es 0,2; calcule el cambio que experimenta el
diámetro bajo la acción de este esfuerzo.

27. Mg. John Cubas Sánchez 27
6. Un alambre de cobre de 4 m de longitud y 1 mm de diámetro es sometido a la siguiente
prueba. Se le aplica inicialmente una carga de 20 N para mantenerlo tirante. A
continuación se lee la posición del extremo inferior del alambre, obteniéndose la siguiente
tabla:
a. Construya una gráfica con estos valores, poniendo en las abscisas los aumentos de longitud
y en las ordenadas las cargas adicionales.
b. Calcule el valor del Módulo de Young
c. ¿Cuál es el esfuerzo en el límite de proporcionalidad?
Cargas adicionales (N) Lectura en la escala (cm)
0 3,02
10 3,07
20 3,12
30 3,17
40 3,22
50 3,27
60 3,32
70 4,27

28. Mg. John Cubas Sánchez 28
a. Gráfica Fuerza vs posición
3,02
3,07
3,12
3,17
3,22
3,27
3,32
4,27
0
10
20
30
40
50
60
70
80
3 3,5 4 4,5
Fuerza(N)
Posición(cm)
Límite de proporcionalidad
Lo = 4 m
r = 0,5 x 10 – 3 m

29. Mg. John Cubas Sánchez 29
b. Módulo de Young
NF 102030 
mxcmx 4
10505,012,317,3 

LA
LF
Y o



2
rA 
 23
105,0 
 xA  27
1086,7 mxA 

47
1051086,7
410


xxx
x
Y
PaxY 11
1002,1
b. Esfuerzo en el límite de
proporcionalidad
mxcmL 3
1033,002,332,3 

oL
L
 4
3
105,7
4
103 

 x
x


e
Y e Y
411
105,71002,1 
 xxxprope
Paxprop
7
1065,7e