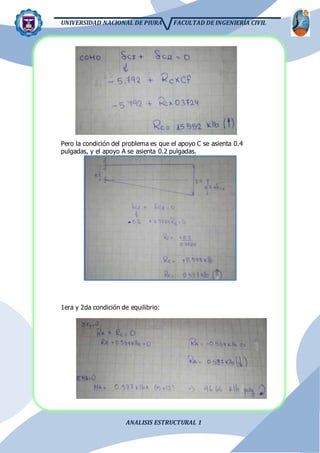
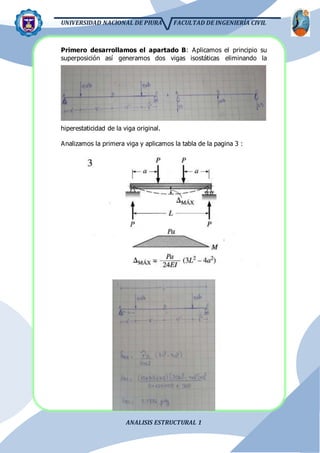
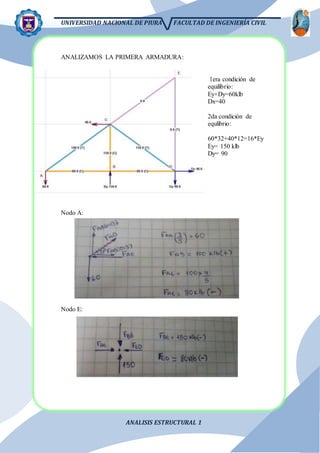
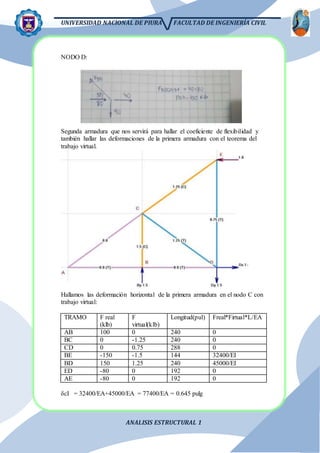
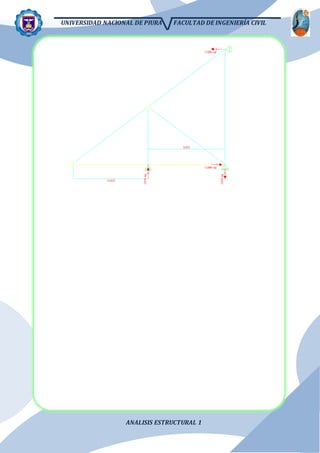
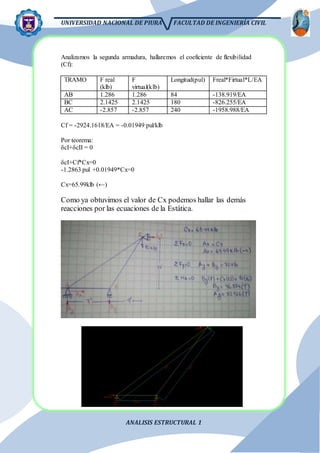
El documento presenta el análisis estructural de una viga con apoyos que se asientan distintas distancias. Se resuelve el problema aplicando el principio de superposición para dividir la viga en partes isostáticas. Se calculan las reacciones, deformaciones y diagramas de corte y momento. También se analiza el efecto de la temperatura y el asiento de un apoyo.