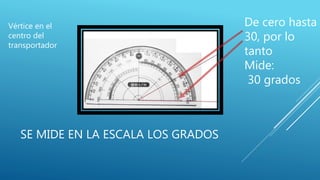
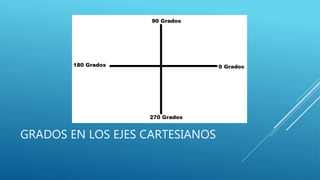
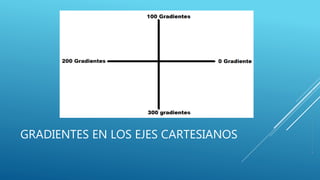
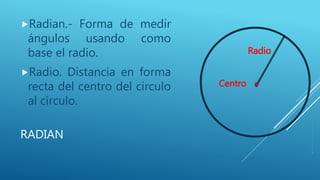
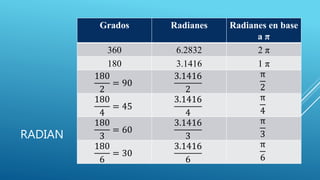
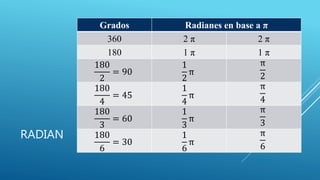
El documento habla sobre la medición de ángulos. Explica que un ángulo se forma entre dos líneas que convergen en un punto llamado vértice. Los ángulos se miden en grados, gradientes o radianes usando un transportador, y cada unidad tiene su propia forma de división del círculo. También cubre la conversión entre grados y radianes.

1. ÁNGULOS
Mediciiones
Unidades

2. ÁNGULO
Un ángulo se forma entre dos
líneas que convergen en un
punto que se le llama vértice.

3. LOS ÁNGULOS SE MIDEN CON UN
TRANSPORTADOR

4. LOS ÁNGULOS SE MIDEN CON UN
TRANSPORTADOR
Centro del
transportador

5. EL VÉRTICE SE COLOCA EN EL CENTRO DEL
TRANSPORTADOR Y SE COLOCA UNA DE LAS
LÍNEAS EN EL CERO DE LA ESCALA
Vértice en el
centro del
transportador
Cero de la
escala

6. SE MIDE EN LA ESCALA LOS GRADOS
Vértice en el
centro del
transportador
De cero hasta
30, por lo
tanto
Mide:
30 grados

7. UNIDADES DE MEDICIÓN DE ÁNGULOS
Grados
Gradientes
Radianes

8. GRADOS

9. GRADOS
Los grados se estable-cen
dividiendo un círculo en
360 partes, donde cada
parte es un grado. Y se
mide en sentido contrario
de las manecillas de un
reloj.

10. GRADOS
Los grados se le denominan
sexagesimal debido a que sus
submúltiplos se relacionan en
proporción de 60:
1 Grado equivale 60 minutos.
1 minuto tiene 60 segundos.

11. GRADOS EN LOS EJES CARTESIANOS

12. GRADIENTES

13. GRADIENTE
Los gradientes se establecen
dividiendo un círculo en 400
partes, donde cada parte es
un gradiente. Y se mide en
sentido contrario de las
manecillas de un reloj.

14. GRADIENTES EN LOS EJES CARTESIANOS

15. RADIANES

16. RADIAN
Radian.- Forma de medir
ángulos usando como
base el radio.
Radio. Distancia en forma
recta del centro del circulo
al círculo.
Radio
Centro

17. RADIAN
Radio Ángulo
Radian

18. DEFINICIÓN
Un radian es el ángulo que se
forma cuando sobre el
perímetro del ángulo es la
distancia equivalente de un
radio
Radian
Radio
Radio

19. RADIAN
Como el diámetro equivale 3.1416 veces en el
perímetro, por lo tanto el radio equivale el doble 6.2832
veces en el perímetro, y por eso en una circunferencia
tiene 6.2832 Radianes en 360 Grados:
360 Grados = 6.2832 Radianes
Debido a que es un número irracional y no es un valor
exacto, por simplicidad:
360 Grados = 2 π Radianes

20. RADIAN
Grados Radianes Radianes en base
a π
360 6.2832 2 π
180 3.1416 1 π
180
2
= 90
3.1416
2
π
2
180
4
= 45
3.1416
4
π
4
180
3
= 60
3.1416
3
π
3
180
6
= 30
3.1416
6
π
6

21. RADIAN
Grados Radianes en base a π
360 2 π 2 π
180 1 π 1 π
180
2
= 90
1
2
π
π
2
180
4
= 45
1
4
π
π
4
180
3
= 60
1
3
π
π
3
180
6
= 30
1
6
π
π
6

22. MEDICIÓN DE ÁNGULOS
Conversión entre:
radianes y Grados

23. CONVERSIÓN DE GRADOS A RADIANES
Se tienen 30 grados equivalen a ? Radianes
30 𝐺𝑟𝑎𝑑𝑜𝑠
π 𝑅𝑎𝑑𝑖𝑎𝑛𝑒𝑠
180 𝐺𝑟𝑎𝑑𝑜𝑠
=
30π 𝑅𝑎𝑑𝑖𝑎𝑛
180
Simplificando:
30π 𝑅𝑎𝑑𝑖𝑎𝑛
180
=
3π 𝑅𝑎𝑑𝑖𝑎𝑛
18
=
π 𝑅𝑎𝑑𝑖𝑎𝑛
60
Valor numérico:
3.1416 𝑅𝑎𝑑𝑖𝑎𝑛
6
= 0.5236 𝑅𝑎𝑑𝑖𝑎𝑛

24. CONVERSIÓN DE RADIANES A GRADOS
Se tienen 4.5 Radianes equivalen a ? Grados
4.5 𝑅𝑎𝑑𝑖𝑎𝑛
180 𝐺𝑟𝑎𝑑𝑜𝑠
π 𝑅𝑎𝑑𝑖𝑎𝑛𝑒𝑠
=
4.5 180 𝐺𝑟𝑎𝑑𝑜𝑠
π
Valor numérico:
810 𝐺𝑟𝑎𝑑𝑜𝑠
3.1416
= 257.83𝐺𝑟𝑎𝑑𝑜𝑠