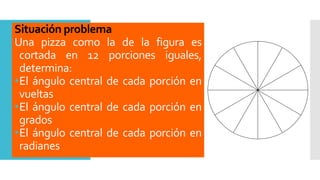
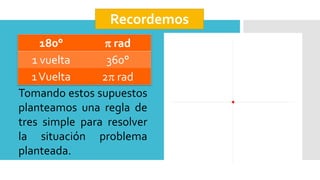
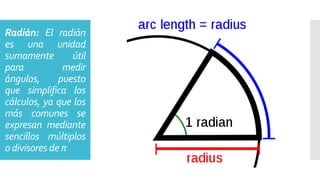
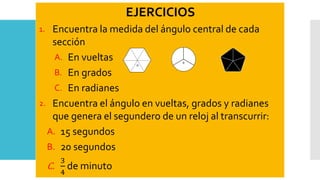
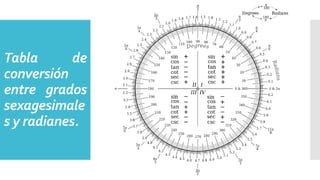
Este documento presenta diferentes sistemas de medición de ángulos, incluyendo grados, radianes y vueltas. Explica que los radianes son la unidad angular natural en trigonometría, con una circunferencia completa igual a 2π radianes. También proporciona una tabla de conversión entre grados y radianes, y presenta ejercicios para practicar conversiones entre las diferentes unidades de medida de ángulos.

1. Sistemas de Medición
deÁngulos
GIMNASIO CAMPESTRE
GRADOS 9´S

2. Objetivos
Formativo
Participar
activamente en los
procesos de
adquisición de
nuevos
conocimientos
interactuando con
los demás
compañeros y con
el docente en todas
las actividades.
Cognitivo
Reconoce el grado
sexagesimal, el
radián y las vueltas
o revoluciones
como unidades de
medidas angulares
y hace
transformaciones
entre ellas.

3. PRECONCEPTOS NECESARIOS PARA LA
CLASE
¿Qué concepto tienes de lo que es un
radián?
¿Cuántos grados tiene un ángulo de una
vuelta?
¿Cuántos radianes tiene un ángulo de
una vuelta?
¿Cuántos grados y cuántos radianes tiene
un ángulo de media vuelta

4. Situación problema
Una pizza como la de la figura es
cortada en 12 porciones iguales,
determina:
•El ángulo central de cada porción en
vueltas
•El ángulo central de cada porción en
grados
•El ángulo central de cada porción en
radianes

5. Recordemos
180°  rad
1 vuelta 360°
1Vuelta 2 rad
Tomando estos supuestos
planteamos una regla de
tres simple para resolver
la situación problema
planteada.

6. En la medida de ángulos, y por tanto en
trigonometría, se emplean cuatro
unidades, si bien la más utilizada en la
vida cotidiana es el Grado sexagesimal,
en matemáticas es el Radián la más
utilizada, y se define como la unidad
natural para medir ángulos, el Grado
centesimal se desarrolló como la unidad
más próxima al sistema decimal, se usa
en topografía, arquitectura o en
construcción.

7. Radián: unidad angular natural en
trigonometría, será la que aquí utilicemos.
En una circunferencia completa hay 2π
radianes.
Grado sexagesimal: unidad angular que
divide una circunferencia en 360 grados.
Grado centesimal: unidad angular que
divide la circunferencia en 400 grados
centesimales.
Horario: su unidad de medida es el ángulo
de 1 hora, que equivale a la sexta parte del
ángulo recto.

8. 1 radián:Un radián
es la unidad de
medida de un
ángulo con vértice
en el centro de un
círculo cuyos lados
son cortados por el
arco de la
circunferencia, y que
además dicho arco
tiene una longitud
igual a la del radio.

9. Radián: El radián
es una unidad
sumamente útil
para medir
ángulos, puesto
que simplifica los
cálculos, ya que los
más comunes se
expresan mediante
sencillos múltiplos
o divisores de π

11. EJERCICIOS
1. Encuentra la medida del ángulo central de cada
sección
A. En vueltas
B. En grados
C. En radianes
2. Encuentra el ángulo en vueltas, grados y radianes
que genera el segundero de un reloj al transcurrir:
A. 15 segundos
B. 20 segundos
C.
3
4
de minuto

 

12. EJERCICIOS
Convierte a la unidad indicada
A. 300° en radianes
B. 75°en radianes
C.
1
6
π radianes en grados
D.
2
3
π radianes en grados
E.
1
4
π radianes en vueltas
F. 0.75 vueltas en radianes
G. 72º en radianes
H.
3
4
π radianes en vueltas
I.
7
12
π radianes en grados

13. Tabla de
conversión
entre grados
sexagesimale
s y radianes.

14. AyudasWebs
(Clic en los enlaces)
1. Sistemas de medidas angulares, ejercicios resueltos
2. Trigonometría I: Razones trigonométricas y fórmulas
3. Circulo unitario y razones trigonométricas
4. Radián y Equivalencia en grados sexagesimales

15. Gracias…