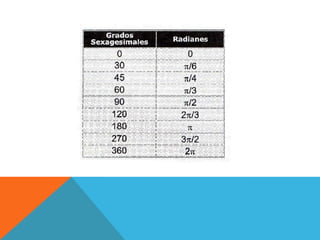
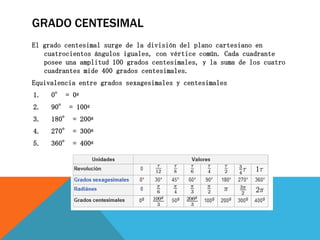
El documento explica cómo convertir entre las unidades de medida de ángulos grados y radianes. Define los grados sexagesimales y centesimales, y los radianes. Explica que para convertir entre grados y radianes se usa la equivalencia de que 180 grados equivalen a π radianes, y provee ejemplos de conversiones entre estas unidades.

1. TRIGONOMETRÍA Y GEOMETRÍA
DE GRADOS A RADIANES Y VICEVERSA
Miembros del equipo
 Luis Jaime De La Lama
Castro
 Gabriel Balbuena Cerón

2. QQQ (Qué veo, Qué no veo, Qué infiero)
• Método de aprendizaje Autónomo
Es la identificación de las ideas principales de un texto, respetando
las ideas del autor. Es un procedimiento derivado de la
comprensión de la lectura.
CARACTERÍSTICAS
 Leer de manera general el tema o texto
 Seleccionar las ideas más importantes
 Buscar el significado de las palabras o términos desconocidos
 Eliminar la información poco relevante
 Redactar el informe final conectando las ideas principales.

3. UNIDADES ANGULARES
En la medición de los ángulos en la trigonometría se ocupa 2unidades que
son:
1. Radian
2. Grado Sexagesimal

4. RADIAN
El radián es la unidad de ángulo plano en
el Sistema Internacional de Unidades.
Representa el ángulo central en
una circunferencia y abarca un arco cuya
longitud es igual a la del radio. Su
símbolo es rad.
1. La equivalencia entre grados
sexagesimales y radianes es: π rad =
180°

5. El valor de Pi y el resultado de su división con 180 no debe de ser
redondeado ya que no dará los valores exactos tanto en
conversión de radianes a grados y grados en radianes.
1 radián = 180/Pi=57.29577951 Grados (°)
1 grado = Pi/180=0.017453292 Radianes (rad)
Pi=3,141592654

7. GRADO SEXAGESIMAL
El grado sexagesimal, como unidad del sistema de medida
de ángulos sexagesimal, está definido partiendo de que
un ángulo recto tiene 90° (90 grados sexagesimales), y
sus divisores: el minuto sexagesimal y el segundo
sexagesimal, están definidos del siguiente modo:
1 ángulo recto = 90° (grados sexagesimales).
1 grado sexagesimal = 60′ (minutos sexagesimales).
1 minuto sexagesimal = 60″ (segundos sexagesimales)

8. RELACIÓN DE GRADOS
A RADIANES EN LA GEOMETRÍA
Que veo Que no veo Que infiero

9. GRADO CENTESIMAL
El grado centesimal surge de la división del plano cartesiano en
cuatrocientos ángulos iguales, con vértice común. Cada cuadrante
posee una amplitud 100 grados centesimales, y la suma de los cuatro
cuadrantes mide 400 grados centesimales.
Equivalencia entre grados sexagesimales y centesimales
1. 0° = 0g
2. 90° = 100g
3. 180° = 200g
4. 270° = 300g
5. 360° = 400g

10.  Un ángulo: es la figura formada por dos semirrectas que se
interceptan en un punto. Las semirrectas son los lados del ángulo
y el punto de intersección en su vértice

12. Para convertir de grados a radianes o viceversa, partimos de que
180o equivalen a π radianes; luego planteamos una regla de tres y
resolvemos.
EJEMPLO A: Convertir 38o a radianes.
EJEMPLO B: Convertir 2.4 radianes a grados.
EJEMPLO C: Convertir 90° a radianes
EJEMPLO D: Convertir 180° a grados centesimales
EJEMPLO E: Convertir 43.18 a grados centesimales