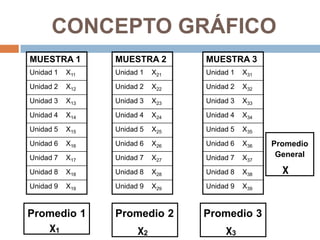
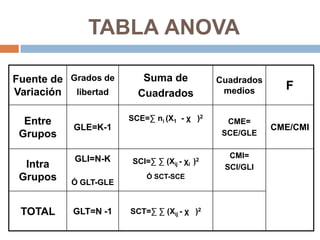
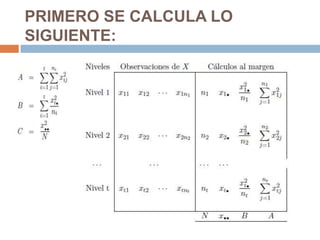
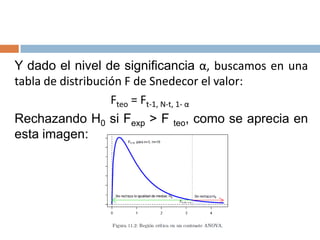
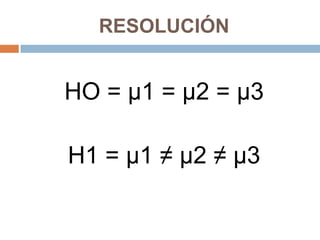
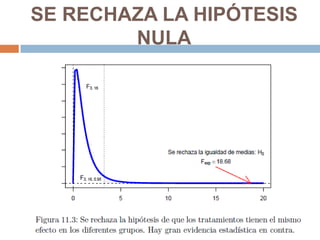
El análisis de varianza (ANOVA) es una técnica estadística que compara las medias de 3 o más poblaciones para determinar si son significativamente diferentes. ANOVA asume que las muestras provienen de distribuciones normales con igual varianza y que son independientes. Calcula la varianza entre grupos y dentro de grupos para determinar si hay más variabilidad entre las medias de los grupos que dentro de cada grupo.

1. ANÁLISIS DE LA
VARIANZA
(ANOVA)

2. DEFINICIÓN
Técnica de prueba de hipótesis paramétrica
que tiene como objetivo básico verificar si hay
diferencias
estadísticamente
significativas
entre las medias de más de 2 poblaciones.

3. CARACTERÍSTICAS Y
SUPUESTOS
Compara 3 ó más medias poblacionales, si
son iguales.
 Evita la propagación del error.
 Las muestras provienen de poblaciones con
un distribución normal.
 Las
desviaciones
estándar
de
las
poblaciones son iguales.
 Las muestras son independientes.


4. CONCEPTO GRÁFICO
MUESTRA 1
MUESTRA 2
MUESTRA 3
Unidad 1
X11
Unidad 1
X21
Unidad 1
X31
Unidad 2
X12
Unidad 2
X22
Unidad 2
X32
Unidad 3
X13
Unidad 3
X23
Unidad 3
X33
Unidad 4
X14
Unidad 4
X24
Unidad 4
X34
Unidad 5
X15
Unidad 5
X25
Unidad 5
X35
Unidad 6
X16
Unidad 6
X26
Unidad 6
X36
Unidad 7
X17
Unidad 7
X27
Unidad 7
X37
Unidad 8
X18
Unidad 8
X28
Unidad 8
X38
Unidad 9
X19
Unidad 9
X29
Unidad 9
X39
Promedio 1
χ1
Promedio 2
χ2
Promedio 3
χ3
Promedio
General
χ

5. VARIANZA TOTAL
La variación TOTAL es la que toma en cuenta la
variación entre TODAS las unidades tomando
en cuenta la diferencia a la gran media
∑ (X11 - χ )2 + (X12 - χ )2 + … + (X39 - χ )2



Este valor se conoce como LA SUMA DE
CUADRADOS (Que es la parte superior de la
varianza)
Cada dato es reconocido con dos subíndices, el
primero indica el grupo y de manera se denota
con la letra “i” y la segunda que es la unidad
dentro del grupo y se denota con la letra “j”

6. VARIANZA ENTRE
GRUPOS

La Varianza ENTRE GRUPOS compara
las medias de cada Grupo con la gran
Media
∑ n1 (X1 - χ )2 + n2 (X2 - χ )2 + n3 (X3 χ )2

Es la varianza que mide las diferencias
entre grupos o muestras habitualmente el
número de grupos se denota de manera
general con la letra K

7. VARIANZA INTRA-GRUPOS

La varianza INTRA GRUPOS considera la
variación que hay dentro de cada grupo
∑ (X11 – χ1 )2 + (X12 – χ1 )2 + … + (X19 – χ1 )2
+
 Para cada Grupo
∑ (X21 – χ2 )2 + (X22 – χ2 )2 + … + (X29 – χ2 )2
+
∑ (X31 – χ3 )2 + (X32 – χ3 )2 + … + (X39 – χ3 )2

8. TABLA DE ANOVA
Los datos de las varianzas se resumen en
lo que se llama “LA TABLA DE ANÁLISIS
DE VARIANZA”
 Que reúne los valores y los llamados
grados de libertad.


9. TABLA ANOVA
Fuente de Grados de
Variación libertad
Entre
Grupos
Intra
Grupos
TOTAL
GLE=K-1
GLI=N-K
Ó GLT-GLE
GLT=N -1
Suma de
Cuadrados
SCE=∑ ni (X1 - χ )2
SCI=∑ ∑ (Xij - χi
)2
Ó SCT-SCE
SCT=∑ ∑ (Xij - χ )2
Cuadrados
medios
F
CME=
SCE/GLE
CME/CMI
CMI=
SCI/GLI

10. PRIMERO SE CALCULA LO
SIGUIENTE:

11. Entonces las cantidades admiten una
expresión muy sencilla:
SCE = B-C  SE2 = SCE/t-1
SCT = A-C
SCD = A-B  SD2 = SCD/N-t
Calculamos:
Fexp = S2E/S2D


12. Y dado el nivel de significancia α, buscamos en una
tabla de distribución F de Snedecor el valor:
Fteo = Ft-1, N-t, 1- α
Rechazando H0 si Fexp > F teo, como se aprecia en
esta imagen:

13. EJEMPLO
Se aplican 4 tratamientos distintos a 4 grupos de
5 pacientes, obteniéndose los resultados de la
tabla que se adjunta. Queremos saber si se
puede concluir que todos los tratamientos tienen
el mismo efecto.

14. RESOLUCIÓN
HO = μ1 = μ2 = μ3
H1 = μ1 ≠ μ2 ≠ μ3

15. Calculando:
En conclusión, el Fexp > Fteo, por tanto se ha de
rechazar la igualdad de efectos de los
tratamiento.

16. SE RECHAZA LA HIPÓTESIS
NULA