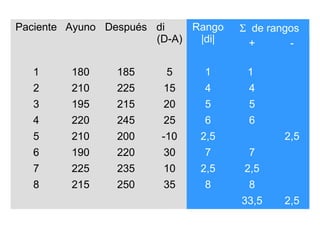
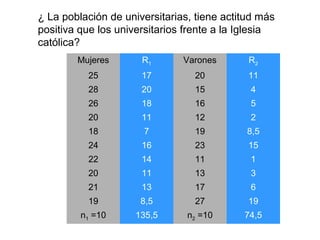
Este documento describe las pruebas no paramétricas, las cuales no dependen de la forma de la distribución poblacional y se usan cuando las variables no cumplen con los supuestos de las pruebas paramétricas. Explica dos pruebas no paramétricas comúnmente usadas: la prueba signo-rango de Wilcoxon, para comparar dos muestras relacionadas, y la prueba suma de rangos de Wilcoxon, para comparar dos poblaciones independientes. Proporciona ejemplos detallados de cómo aplicar cada prueba

1. PRUEBAS NO
PARAMÉTRICAS

2. Las pruebas de significación estadística pueden
clasificarse en:
Paramétricas: Contrastan hipótesis sobre parámetros.
Ejemplos: Pruebas t, z y ANOVA
No paramétricas: Contrastan hipótesis que no son
afirmaciones sobre parámetros y no dependen de
la forma de la distribución poblacional; por este
hecho, se denominan también pruebas de
distribución libre. Ejemplos: Prueba signo rango de
Wilcoxon, prueba suma de rangos de Wilcoxon,
prueba χ2 de Mc Nemar,etc.
A continuación desarrollaremos dos pruebas no
paramétricas muy utilizadas:

3. 1.- Prueba signo - rango de
Wilcoxon
Se usa:
Para comparar dos muestras relacionadas; es
decir, para analizar datos obtenidos mediante el
diseño antes-después (cuando cada sujeto sirve
como su propio control) o el diseño pareado
(cuando el investigador selecciona pares de
sujetos y uno de cada par, en forma aleatoria, es
asignado a uno de dos tratamientos). Pueden
existir además otras formas de obtener dos
muestras relacionadas.

4. 

Cuando la variable es:
Cuantitativa medida en escala ordinal.
Cuantitativa medida en escala de intervalo o de
razón, pero las diferencias (di) de los pares de
datos no se distribuyen normalmente. En este
caso, se usa en lugar de la prueba t de Student
para dos muestras relacionadas o “t pareada”.
Ejemplo: Los datos corresponden a una muestra
de 8 pacientes varones de 45 a 55 años de
edad. Son lecturas de colesterol total tomadas
tras 12 horas de ayuno y repetida una hora
después de comer.¿Hubo un incremento
significativo de los niveles de colesterol después
de la comida?

5. Paciente Ayuno Después di
Rango
(D-A)
|di|
Σ de rangos
+
-
1
180
185
5
1
1
2
210
225
15
4
4
3
195
215
20
5
5
4
220
245
25
6
6
5
210
200
-10
2,5
6
190
220
30
7
7
7
225
235
10
2,5
2,5
8
215
250
35
8
8
2,5
33,5
2,5

6. Solución:
a.- Hipótesis
H0 : No hubo incremento significativo de colesterol total
después de la comida.
H1 : Hubo incremento significativo de colesterol total
después de la comida.
b.- Cálculo del contraste T:
T = 33,5 (ó T = 2,5)
c.- Cálculo de zT
Con:
n(n + 1)
μT =
4
Luego :
n(n + 1)(2n + 1)
σT =
24
T − μT
zT =
σT

7. En este caso n = 8 (ya que no hubo ningún par de datos
iguales)
8(9)
8(9)(17 )
µ =
T
= 18 σ =
T
= 7,14
4
24
33,5 −18
Luego : zT =
= 2,17
7,14
d.- Valor de p:
p = 1 – 0,9850
p = 0,015
e.- Decisión y Conclusión:
Siendo p = 0,015 (< 0,05), se rechaza la hipótesis nula.
Se concluye que hubo un incremento estadísticamente
significativo de los niveles de colesterol después de la
comida (p = 0,015).

8. 2.- Prueba suma de rangos de
Wilcoxon .
Se usa:
Para comparar dos poblaciones independientes.
Cuando la variable es:
 Cuantitativa medida en escala ordinal.
 Cuantitativa medida en escala de intervalo o de
razón, pero la variable en una o en las dos
poblaciones no tiene distribución normal. En este
caso, se usa en lugar de la prueba t Student para
dos muestras independientes.
Ejemplo: Se tomó una muestra de 10 universitarias y
otra de 10 universitarios para determinar si las mujeres
tenían actitud más positiva que los varones frente a la
Iglesia católica. Los puntajes en un cuestionario de
actitudes fueron:( mayor puntaje, actitud más positiva).

9. ¿ La población de universitarias, tiene actitud más
positiva que los universitarios frente a la Iglesia
católica?
Mujeres
R1
Varones
R2
25
17
20
11
28
20
15
4
26
18
16
5
20
11
12
2
18
7
19
8,5
24
16
23
15
22
14
11
1
20
11
13
3
21
13
17
6
19
8,5
27
19
n1 =10
135,5
n2 =10
74,5

10. Solución:
a.- Hipótesis:
H0 : mediana de puntajes de las mujeres ≤ mediana de
varones.
H1 : mediana de puntajes de las mujeres > mediana de
varones.
En otros términos:
H0: Las mujeres no tienen actitudes más positivas que
los varones frente a la Iglesia Católica .
H1: Las mujeres tienen actitudes más positivas que los
varones frente a la Iglesia Católica.
b.- Suma de rangos (W)
W = suma de rangos.
W = 74,5

11. c.- Cálculo de zW
n1(n1 + n2 + 1) 10(21)
µW =
=
= 105
2
2
n1 = tamaño menor
n1n2(n1 + n2 + 1)
σW =
= 13,23
12
W − µW
Luego : zW =
σW
74,5 − 105
zW =
= −2,31
13,23

12. d.- Valor de p
Siendo la prueba unilateral:
p = 0,0104
e.- Decisión y Conclusión:
Decisión: Siendo p = 0,0104 ( < 0,05), se rechaza la
hipótesis nula.
Conclusión: Las mujeres tienen actitudes más positivas
que los varones frente a la Iglesia Católica (p = 0,0104).
La prueba explicada proporciona el mismo resultado
que la Prueba U de Mann-Whitney.