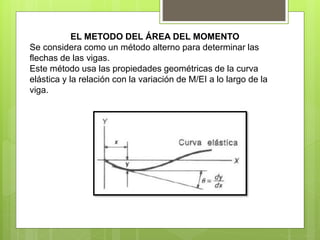
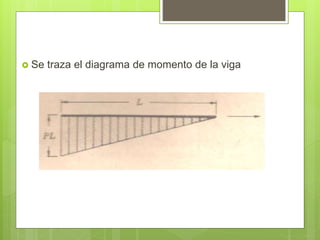
Este documento describe el método del área de momentos para determinar la flecha en vigas. El método utiliza las propiedades geométricas de la curva elástica y la relación entre la variación del momento flector dividido por el módulo de elasticidad-inercia a lo largo de la viga. Incluye los teoremas del área de momentos y el proceso de cálculo de la flecha en un punto mediante la comparación del área bajo la curva del momento flector entre dos puntos de la viga.

1. DEFORMACION DE
VIGAS. METODO
DEL ÁREA DE
MOMENTOS.

2. LA DEFLEXION DE UNA VIGA ES EL MOVIMIENTO
(DESVIACCION) DE UN PUNTO SITUADO SOBRE LA ELASTICA,
CON RESPECTO A SU POSICION SIN CARGA.
LA PENDIENTE DE UNA VIGA SE DEFINE COMO LA
PENDIENTE DE LA TANGENTE A LA ELASTICA DE UN PUNTO
CUALQUIERA.
LA ELASTICA DE UNA VIGA ES LA FORMA QUE TOMA EL EJE
NEUTRO CUANDO SE CARGA LA VIGA. CADA PUNTO SITUADO
SOBRE LA ELASTICA TENDRA UN DEFLEXION Y, Y UNA
PENDIENTE dy/dx

3. EL METODO DEL ÁREA DEL MOMENTO
Se considera como un método alterno para determinar las
flechas de las vigas.
Este método usa las propiedades geométricas de la curva
elástica y la relación con la variación de M/EI a lo largo de la
viga.

4. EL PRIMER TEOREMA DEL ÁREA DE
MOMENTOS.
El Angulo de las tangentes en A y B es igual al área del
diagrama de momentos flectores entre esos dos puntos,
divididos por el producto EI.
se expresa por la ecuación.

5. EL SEGUNDO TEOREMA DEL ÁREA DE
MOMENTOS.
La distancia en vertical entre el punto B de una elástica y la
tangente trazada por el punto A es igual al momento respecto a
la vertical por B del área del diagrama de momentos flectores
entre A y B divididos por el EI.
se expresa por la ecuación

6. PROCESO DEL AREA DE MOMENTOS.
La determinación de las flechas en un punto dado de una viga
cargada se hace siguiendo el proceso siguiente.
1.- se determina las reacciones de la viga. En el caso de una viga en
voladizo se puede suprimir frecuentemente este paso.
2.- se dibuja una curva elástica aproximada. Debe estar de acuerdo
con las condiciones conocidas con los apoyos, tales como pendiente
nula o flecha nula.

7. 3.- se traza el diagrama de momentos flectores de la viga.
Frecuentemente conviene trazar el diagrama de momentos por partes.
4.- se eligen puntos A y B apropiados y se traza una tangente en unos de
ellos, por ejemplo, en A a la elástica supuesta.
5.- se calcula el desplazamiento del punto B desde la tangente en A por el
segundo teorema del área de momentos.

8. COMPARACION DE LOS METODOS DEL AREA DE
MOMENTO Y DE LA DOBLE INTEGRACION.
Para obtener solo
la flecha es
conveniente usar
el MÉTODO DE
ÁREA MOMENTO.
Si se quiere
obtener toda la
ecuación de la
elástica se utiliza
el MÉTODO DE
LA DOBLE
INTEGRACIÓN.

9. La viga en voladizo de la figura esta sometido a la
carga aislada P aplicada en su extremo libre.
Determinar la flecha en el punto de aplicación de la
carga

10.  Se traza el diagrama de momento de la viga

11.  Trazar una tangente a la elástica en el punto A
En este caso en particular el desplazamiento del
punto B y la tangente A es la flecha buscada.

12.  Se aplica el segundo teorema del área de momentos, el
desplazamiento de B a la tangente trazada A esta dado por el momento
respecto a la vertical por B del área bajo el diagrama de momentos
flectores dividos por el producto EI
El teorema del area de momentos se convierte en

13. 8
200kg
Δ
B
A
Tg en A
200kg
M= 1600kg.m

14. 200
kg
𝜀 𝑀 = −200𝑥 + 1600 + 𝑀 = 0
M = 200𝑥 − 1600 𝐾𝑔𝑚
0 8
dc
𝐸𝐼Δ = 𝑎𝑟𝑒𝑎 ∗ 𝑑𝑐
800 ∗ 160000
2
∗
2
3
∗ 800 = 64000000 ∗ 533.33 =
3.413312𝑥1010
𝐸𝐼
∆=
3.413312𝑥1010
(2 ∗ 106)(11862.59)
= −0.00539511𝑐𝑚