Este documento describe gráficas de control para atributos, específicamente la gráfica p que monitorea la fracción defectuosa de un proceso. Explica cómo construir e interpretar la gráfica p, incluyendo el cálculo de los límites de control y la selección del tamaño de muestra. También cubre el análisis de patrones para identificar procesos fuera de control. Presenta dos ejemplos numéricos para ilustrar el uso de la gráfica p con tamaños de muestra constantes y variables.

1. INGENIERIAY CONTROL DE LA CALIDAD
CONTROL ESTADISTICO DEL PROCESO
GRAFICAS DE CONTROL PARAATRIBUTOS
César A. Acosta-Mejía

2. GRAFICAS DE CONTROL PARAATRIBUTOS
Atributo: característica de calidad que el bien o servicio posee o no.
Ejemplos:
1. El Color de la carrocería de un automovil
2. El acabado superficial de una lámina
Un producto defectuoso puede tener uno o más defectos

3. GRAFICOS DE CONTROL PARAATRIBUTOS
CLASIFICACION
Gráficos de control para unidades defectuosas
• La gráfica p fracción defectuosa
• La gráfica np número de unidades defectuosas
Gráficos de control para defectos
• La gráfica c número de defectos.
• La gráfica u número de defectos por unidad.

4. GRAFICOS DE CONTROL PARAATRIBUTOS
CLASIFICACION
Gráficos de control para unidades defectuosas muestras de:
• La gráfica p fracción defectuosa
• La gráfica np número de unidades defectuosas (tamaño constante)
Gráficos de control para defectos
• La gráfica c número de defectos. (tamaño constante)
• La gráfica u número de defectos por unidad.

5. GRAFICA DE CONTROL p
• Sea xi el número de unidades defectuosas observadas en muestras de
tamaño ni .
• Sea pi la fracción defectuosa de la muestra i (de tamaño ni)
pi = Número de defectuosos xi
Número de Artículos ni
• Se grafica los valores de pi y se verifica que
se encuentren entre los límites de control
no se observan patrones sistemáticos
• En caso de haber puntos fuera de control, los límites se recalculan

6. GRAFICA DE CONTROL p
Si el proceso está estable con fracción defectuosa constante p; y si las
observaciones se pueden considerar independientes entonces:
X : # de defectuosos en una muestra de tamaño n  Binomial (n,p)
La distribución binomial se aproxima por la distribución normal si np > 5
X  Normal (  = np,  =  np(1-p) )
y los límites de control son: E [X/n]  3 DS [X/n]
p  3  p(1-p)/ n

7. GRAFICA DE CONTROL p
• Esta gráfica controla si el parámetro p de la distribución binomial
permanece constante
• En un solo gráfico se puede controlar una, varias, o todas las
características de calidad del producto

8. GRAFICA DE CONTROL p
Cálculo de los límites de control
Los Límites de control son: p ± 3
(binomial  normal)
Si p no se conoce, se le estima
a partir de m muestras previas, con
p p
n
( )
1
p
x
n
m
m




9. GRAFICA DE CONTROL p
Cálculo de los límites de control
Los Límites de control son: p ± 3
(binomial  normal)
Si p no se conoce, se le estima
a partir de m muestras previas, con
Note que si n varía
los límites de control no seran constantes p ± 3
p p
n
( )
1
p
x
n
m
m



i
n
p
p )
1
( 

10. GRAFICA DE CONTROL p
los datos siguen una distribución binomial
Estadístico (x/n)
Límite Superior de Control (LSC)
Línea Central
Límite Inferior de Control (LIC)
muestra
X es una v. a. binomial(n, p)

11. El proceso está estable o en control (estadístico) si la distribución binomial se
mantiene constante en el tiempo
tiempo
La distribucion binomial permanece constante si p no cambia
X/n
GRAFICA DE CONTROL p
los datos siguen una distribución binomial

12. GRAFICA DE CONTROL p
Selección del tamaño de muestra n
• La binomial se aproxima por la distribución normal si np > 5
por tanto n > 5 / p

13. GRAFICA DE CONTROL p
Selección del tamaño de muestra n
• La binomial se aproxima por la distribución normal si np > 5
por tanto n > 5 / p
• Si se desea asegurar un LIC entonces p - 3  p(1-p)/ n > 0
por tanto n > 9 (1-p) / p

14. GRAFICA DE CONTROL p
Selección del tamaño de muestra n
• La binomial se aproxima por la distribución normal si np > 5
por tanto n > 5 / p
• Si se desea asegurar un LIC entonces p - 3  p(1-p)/ n > 0
por tanto n > 9 (1-p) / p
• Si el proceso tiene fracción p0 y se desea detectar que la fracción ha
cambiado a p1 con un 50% de probabilidad entonces
x/n
LSC p1
p0 p0

15. GRAFICA DE CONTROL p
Selección del tamaño de muestra n
• La binomial se aproxima por la distribución normal si np > 5
por tanto n > 5 / p
• Si se desea asegurar un LIC entonces p - 3  p(1-p)/ n > 0
por tanto n > 9 (1-p) / p
• Si el proceso tiene fracción p0 y se desea detectar que la fracción ha
cambiado a p1 con un 50% de probabilidad entonces
LSC = p1
p0 + 3  p0 (1-p0 )/ n = p1 p1
 n = 3  p0 (1-p0 ) / (p1 - p0)
n = 9 p0 (1-p0 ) / (p1 - p0)2

16. GRAFICA DE CONTROL p
Selección del tamaño de muestra n
• La binomial se aproxima por la distribución normal si np > 5
por tanto n > 5 / p
• Si se desea asegurar un LIC entonces p - 3  p(1-p)/ n > 0
por tanto n > 9 (1-p) / p
• Si el proceso tiene fracción p0 y se desea detectar que la fracción ha
cambiado a p1 con un 50% de probabilidad entonces
LSC  p1
p0 + 3  p0 (1-p0 )/ n  p1
 n  3  p0 (1-p0 ) / (p1 - p0)
n  9 p0 (1-p0 ) / (p1 - p0)2

17. La compañía ABC fabrica cortadoras de césped. La producción diaria es de
aproximadamente 200 cortadoras. Se ha decidido seleccionar cada día 40 cortadoras al
azar de la línea de proceso para realizar la prueba de calidad. La prueba consiste en
realizar dos ensayos tirando el cordón para ver si el motor arranca. El ingeniero de
producción desea realizar un diagrama p para esta prueba crítica de funcionamiento.
Los datos de mes de marzo con 22 días laborables se muestran en la tabla anexa.
a) Construya la gráfica p e identifique si el proceso está bajo control
b) Estime la fracción defectuosa del proceso suponiendo que se eliminan las causas
especiales de variabilidad
c) Cuántas cortadoras se requieren probar cada día ?
GRAFICA DE CONTROL p
Ejemplo 1

18. GRAFICA DE CONTROL p
Ejemplo 1
Día Numero de artículos Fracción
defectuosa (x/n)
defectuosos (x)
1 2 2/40 = 0.050
2 3 0.075
3 1 0.025
4 4 0.1
5 3 0.075
6 2 0.05
7 1 0.025
8 1 0.025
9 0 0
10 3 0.075
11 2 0.05
12 4 0.1
13 7 0.175
14 2 0.05
15 3 0.075
16 3 0.075
17 2 0.05
18 8 0.2
19 0 0
20 1 0.025
21 3 0.075
22 2 0.05
TOTAL 57

19. a) m = 22 número de muestras
n = 40 tamaño de cada muestra




 M
j
j
M
j
j
n
x
p
1
1
06477
.
0
)
40
(
22
57


 
0
LIC
06477
.
0
LC
1816
.
0
40
06477
.
0
1
06477
.
0
3
06477
.
0
LSC







20. 20
10
0
0.2
0.1
0.0
Sample Number
Proportion P Chart
1
P=0.06477
UCL=0.1815
LCL=0
GRAFICA DE CONTROL p
Stat > Control Charts > P

21. b) El punto p18 cae fuera de los límites de control y el punto p13 está muy próximo. Al
determinar la causa que produjo su comportamiento se les elimina y se recalculan p y
los límites de control (para usarlos durante abril):
Día (i) Numero de artículos
no conformantes en el grupo
Fracción no
conformante
1 2 2/40 = 0.050
2 3 0.075
3 1 0.025
4 4 0.100
5 3 0.075
6 2 0.050
7 1 0.025
8 1 0.025
9 0 0.000
10 3 0.075
11 2 0.050
12 4 0.100
13 7 0.175
14 2 0.050
15 3 0.075
16 3 0.075
17 2 0.050
18 8 0.200
19 0 0
20 1 0.025
21 3 0.075
22 2 0.050
57

22. b) El punto p18 cae fuera de los límites de control y el punto p13 está muy próximo. Al
determinar la causa que produjo su comportamiento se les elimina y se recalculan p y
los límites de control (para usarlos durante abril):
pest = 42 = 0.0525
20(40)
 
0
LIC
0525
.
0
LC
1583
.
0
40
0525
.
0
1
0525
.
0
3
0525
.
0
LSC







23. 20
10
0
0.2
0.1
0.0
Sample Number
Proportion
P Chart con límites revisados
1
1
P=0.0525
UCL=0.1583
LCL=0
GRAFICA DE CONTROL p
P Chart > Estimate > Omit… > 13 18

24. c) Para el próximo mes se utilizarán estos límites revisados para que conforme se
tomen las muestras de cortadoras inmediatamente se verifique si el proceso
permanece en control o no.
Las muestras deberán ser de tamaño n  (5 / 0.0525) = 95.24 para que los
límites sean válidos
GRAFICA DE CONTROL p
Ejemplo 1

25. d) Suponga que la fracción defectuosa real del proceso aumenta a 0.11. Cuál es la
probabilidad de que la gráfica lo detecte en la siguiente muestra ?
GRAFICA DE CONTROL p
Ejemplo 1

26. d) Suponga que la fracción defectuosa real del proceso aumenta a 0.11. Cuál es la
probabilidad de que la gráfica lo detecte en la siguiente muestra ?
Sea X  BIN (n = 40, p = 0.11)
P [x / n > LSC] = P [x / n > 0.1583]
= P [ x > 40 (0.1583)]
= P [ x > 6.332]
= 1 - 0.8555
= 0.145
GRAFICA DE CONTROL p
Ejemplo 1

27. GRAFICA DE CONTROL p
ANALISIS DE PATRONES
El proceso es dado como
fuera de control si se viola
alguna de cuatro reglas:
Test 2 debe decir
“ Eight points in a row ”

28. GRAFICA DE CONTROL p
ANALISIS DE PATRONES
El proceso es dado como
fuera de control si se viola
alguna de cuatro reglas:
Test 2 debe decir
“ Eight points in a row ”
(si el tamaño de las muestras es
variable, los límites de control
no son constantes y entonces
solo aplica la regla Test 1)

29. El ingeniero de calidad de una empresa toma muestras de
la producción diaria con el objeto de elaborar una gráfica
p.
La tabla anexa muestra los rechazos encontrados y la
cantidad de piezas revisadas cada día. Si la fracción
defectuosa de cierto día excede los límites de control el
ingeniero debe inspeccionar al 100% el lote producido.
a) Determine los límites de control y contruya la gráfica
b) Determine los límites de control futuros, suponiendo
que se identifican las causas especiales de los puntos fuera
de control.
GRAFICA DE CONTROL p
Ejemplo 2 – muestra variable
Rechazos Muestra
20 98
18 104
14 97
16 99
13 97
29 102
21 104
14 101
6 55
6 48
7 50
7 53
9 56
5 49
8 56
9 53
9 52
10 51
9 52
10 47
240 1424

30. GRAFICA DE CONTROL p
Ejemplo 2
a) Límites de control
p = xi = 240 = 0.16854
ni 1424
LSCi = 0.168 + 3(0.168)(1-0.168)/ni
LICi = 0.168 - 3(0.168)(1-0.168)/ni

31. GRAFICA DE CONTROL p
Ejemplo 2
a) Límites de control
p = xi = 240 = 0.16854
ni 1424
LSCi = 0.168 + 3(0.168)(1-0.168)/ni
LICi = 0.168 - 3(0.168)(1-0.168)/ni
En este caso los límites de control son variables dependiendo del
tamaño ni de la muestra

32. GRAFICA DE CONTROL p
Ejemplo 2
20
10
0
0.3
0.2
0.1
0.0
Sample Number
Proportion
P Chart for C1
P=0.1685
UCL=0.3324
LCL=0.004728

33. GRAFICA DE CONTROL p
Ejemplo 2
b) Límites de control (después de eliminar punto p6)
pest = xi = 240 - 29 = 0.1596
ni 1424 - 102
LSC = 0.1596 + 3(0.1596)(1-0.1596)/ni
LSC = 0.1596 - 3(0.1596)(1-0.1596)/ni
Rechazos Muestra
20 98
18 104
14 97
16 99
13 97
29 102
21 104
14 101
6 55
6 48
7 50
7 53
9 56
5 49
8 56
9 53
9 52
10 51
9 52
10 47

34. GRÁFICA DE CONTROL np
• Se grafica el número de unidades defectuosas en la muestra
• Es más fácilmente interpretado por el personal al no requerir de
cálculos
• Si el tamaño de muestra es constante, las gráficas p y np muestran el
mismo comportamiento pero a diferente escala

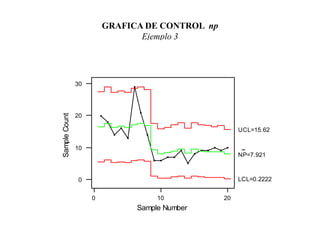
35. GRÁFICA DE CONTROL np
• La gráfica se basa en la aproximación normal a la binomial
• Si X : # de defectuosos en la muestra de tamaño n es
una Variable Binomial (n,p)
entonces X ~ Normal ( np,np (1-p) ) aproximadamente si np 5
• Los límites de control son:
E[X]  3 D.S. [X]
np  3  np (1-p)
• Si el tamaño de muestra es variable, entonces los límites de control así
como la línea central varían de muestra a muestra

36. GRÁFICA DE CONTROL np
• Si el tamaño de muestra no es constante la gráfica p tiene limites de
control variables
LSCi = p + 3p (1-p)/ni
LICi = p - 3p (1-p)/ ni

37. GRÁFICA DE CONTROL np
• Si el tamaño de muestra no es constante la gráfica p tiene limites de
control variables
LSCi = p + 3p (1-p)/ni
LICi = p - 3p (1-p)/ ni
• Si el tamaño de muestra no es constante en la gráfica np, los límites de
control así como la línea central varían de muestra a muestra
LSCi = ni p  3  ni p (1-p)
LICi = ni p - 3  ni p (1-p)

38. El ingeniero de calidad de una empresa toma muestras de
la producción diaria con el objeto de elaborar una gráfica
np.
La tabla anexa muestra los rechazos encontrados y la
cantidad de piezas revisadas cada día. Si el número de
rechazos de cierto día excede los límites de control el
ingeniero debe inspeccionar al 100% el lote producido.
a) Determine los límites de control y contruya la gráfica
b) Determine los límites de control futuros, suponiendo
que se identifican las causas especiales de puntos fuera de
control.
GRAFICA DE CONTROL np
Ejemplo 3 – muestra variable
Rechazos Muestra
20 98
18 104
14 97
16 99
13 97
29 102
21 104
14 101
6 55
6 48
7 50
7 53
9 56
5 49
8 56
9 53
9 52
10 51
9 52
10 47
240 1424

39. GRAFICA DE CONTROL np
Ejemplo 3
a) Límites de control
p = xi = 240 = 0.16854
ni 1424
LSCi = 0.168ni + 3 ni (0.168)(1-0.168)
LCi = 0.168ni
LICi = 0.168ni - 3 ni (0.168)(1-0.168)

40. GRAFICA DE CONTROL np
Ejemplo 3
a) Límites de control
p = xi = 240 = 0.16854
ni 1424
LSCi = 0.168ni + 3 ni (0.168)(1-0.168)
LCi = 0.168ni
LICi = 0.168ni - 3 ni (0.168)(1-0.168)

41. GRAFICA DE CONTROL np
Ejemplo 3
20
10
0
30
20
10
0
Sample Number
Sample
Count
NP=7.921
UCL=15.62
LCL=0.2222

42. GRAFICA DE CONTROL p
Ejemplo 2
0 10 20
0.0
0.1
0.2
0.3
Sample Number
Proportion
P Chart
P=0.1678
UCL=0.3313
LCL=0.004279

43. GRAFICA DE CONTROL p
Ejemplo 2
0 10 20
0.0
0.1
0.2
0.3
Sample Number
Proportion
P Chart
P=0.1678
UCL=0.3313
LCL=0.004279
20
10
0
30
20
10
0
Sample Number
Sample
Count
NP=7.921
UCL=15.62
LCL=0.2222
NP Chart

44. GRAFICAS DE CONTROL PARAATRIBUTOS
Inconvenientes
• Pueden no tener Límite Inferior de Control
• A medida que se mejora el proceso (p disminuye)
se requiere incrementar el tamaño de los subgrupos (n>5/p)
• Tienen desempeño sesgado
(no son muy sensibles para detectar mejoras en p )
• La práctica de identificar patrones sistemáticos ó no aleatorios debe
modificarse ya que la distribución binomial es muy sesgada si p es
pequeño

45. GRAFICAS DE CONTROL PARAATRIBUTOS
• Se utilizan con muestras grandes (a veces cientos ó miles)
Por ejemplo, si p = 0.01 se requieren muestras de tamaño n > 500
• El Costo / unidad de revisar un atributo es menor que el de medir una
característica variable
• Son útiles como medida del desempeño de un taller, departamento,
empresa, etc.
• Generalmente el desempeño mejora después de introducir una gráfica
para atributos pues la gráfica es una representación visual contínua del
desempeño

46. OBJETIVOS DE LAS GRAFICAS DE ATRIBUTOS
• Estimar la fracción defectuosa de producto terminado
• Estimar el Costo estándar de retrabajo (Costos de Calidad)
• Determinar la eficacia de un programa de entrenamiento o de
mantenimiento
• Sugerir dónde utilizar gráficas de control para variables y / o las
gráficas c ó u .