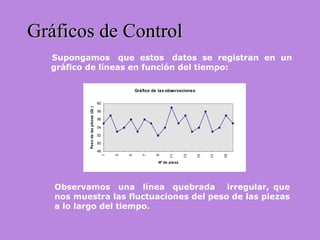
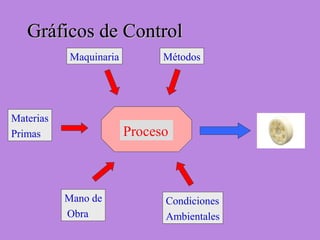
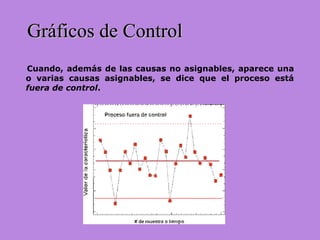
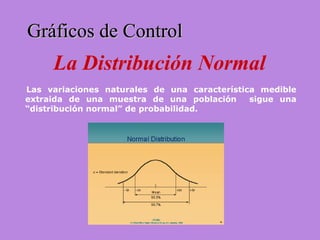
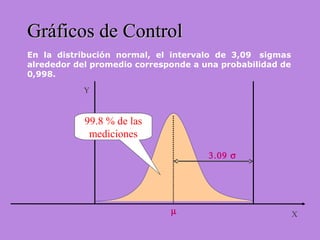
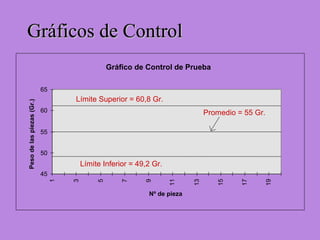
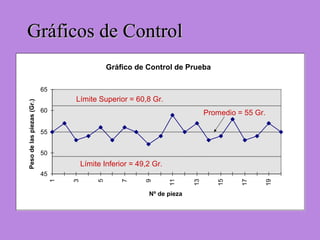
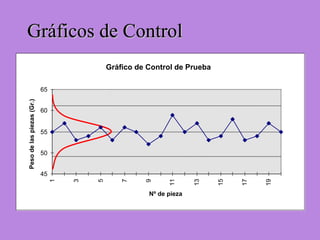
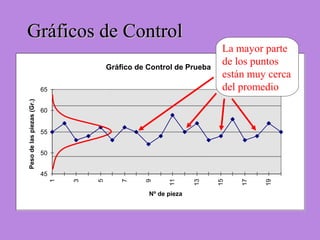
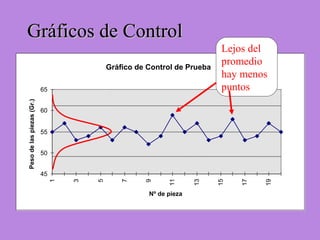
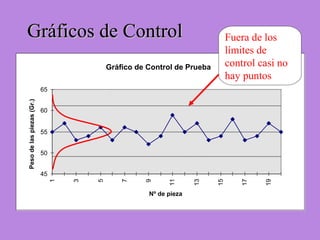
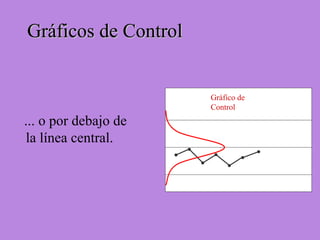
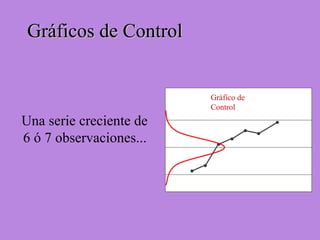
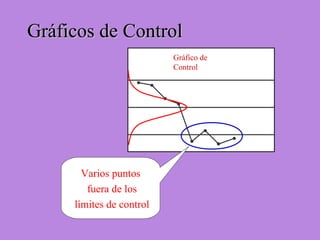
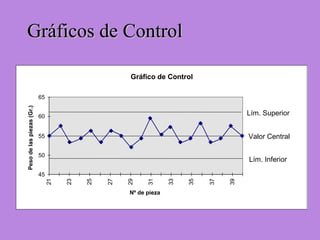
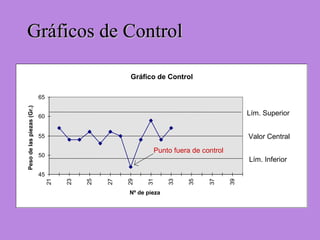
Los gráficos de control son una herramienta para monitorear procesos de producción. Muestran valores de mediciones tomadas durante el funcionamiento de un proceso continuo para identificar cuando el proceso ya no está bajo control estadístico. Se calculan límites de control basados en datos iniciales para determinar si futuras observaciones siguen una distribución normal. Cuando puntos caen fuera de los límites, puede indicar causas asignables que deben ser investigadas para retornar el proceso a un estado de control.