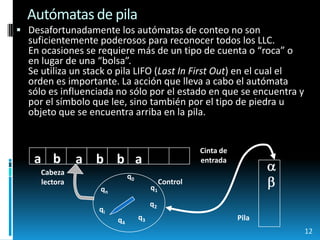
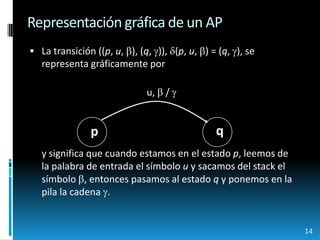
Este documento presenta información sobre teoría de la computación, específicamente sobre lenguajes no regulares y autómatas de pila. Explica conceptos como ambigüedad inherente y transitoria, y cómo los autómatas de pila pueden reconocer lenguajes libres de contexto. También incluye ejemplos de autómatas de pila que reconocen lenguajes palíndromos y lenguajes generados por gramáticas específicas. Finalmente, discute cómo los autómatas de pila pueden simular operaciones de unión

1. INSTITUTO TECNOLOGICO SUPERIOR DE SAN MARTIN TEXMELUCANTEORIA DE LA COMPUTCIONEXPOCISION ELIMINACION DE AMBIGÜEDADESAUTOMATAS PUSH-DOWNLENGUAJES NO REGULARES

2. INTEGRANTESJAVIER COCOLETZISAUL MORALES RODRIGUEZMIGUEL CINTO ALMONTEYESENIA……….

3. ELIMINACIÓN DE AMBIGÜEDADES

4. Una gramática ambigua permite más de una derivación para la misma forma sentencial por lo que también habrá más de un [árbol de derivación] para la misma. Por ello basta con encontrar dos [árboles derivación] distintos para la misma forma sentencial para demostrar que una gramática es ambigua.A continuación se presentan conceptos importantes dentro del estudio de las características de las gramáticas:AMBIGÜEDAD:Sea G = { N , T , P , S } una gramática libre de contexto y sea L(G) el lenguaje generado por esa gramática.

5. TIPOS DE AMBIGÜEDAD: Dentro del estudio de gramáticas existen dos tipos fundamentales de ambigüedad, los cuales son:Ambigüedad Inherente: Las gramáticas que presentan este tipo de ambigüedad no pueden utilizarse para lenguajes de programación, ya que por más transformaciones que se realicen sobre ellas, NUNCA se podrá eliminar completamente la ambigüedad que presentan.Ambigüedad Transitoria: Este tipo de ambigüedad puede llegar a ser eliminada realizando una serie de transformaciones sobre la gramática original. Una vez que se logra lo anterior, la gramática queda lista para ser reconocida por la mayor parte de los analizadores sintácticos. (Se le considera "ambigüedad" porque existen métodos para realizar análisis sintáctico que no aceptan gramáticas con estas características)

6. Eliminación de la ambigüedad– No existe un algoritmo que nos indique si una GIC es ambigua– Existen LIC que sólo tienen GIC ambiguas: inherentemente ambiguos– Para las construcciones de los lenguajes de programación comunesexisten técnicas para la eliminación de la ambigüedad– Ejemplo: causas de ambigüedad en la siguiente gramática• no se respeta la precedencia de operadores• una secuencia de operadores idénticos puede agruparse desde la izquierda y desde laderecha. Lo convencional es agrupar desde la izquierda

7. Una GIC G = (V, T, P, S) es ambigua si existe al menos una cadena w en T *para la que podemos encontrar dos árboles de derivación distintos con la raízetiquetada con S y cuyo resultado es w

8. • Lenguajes independientes del contexto (LIC)• Gramáticas independientes del contexto (GIC)Una gramática libre de contexto en lingüística e informática es una gramática formal en la que cada regla de producción es de la forma:V -> w Donde V es un símbolo no terminal y w es una cadena de terminales y/o no terminales. El término libre de contexto se refiere al hecho de que el no terminal V puede siempre ser sustituido por w sin tener en cuenta el contexto en el que ocurra. Un lenguaje formal es libre de contexto si hay una gramática libre de contexto que lo genera.

9. 9Autómatas de pila(Pushdown autómata)

10. Autómata de conteoAutómata finito determinista con un contador de enteros o “bolsa” en la que se colocan o extraen cuentas o “piedras” en respuesta a un símbolo de entrada. En otras palabras, en cada transición el autómata no sólo selecciona un nuevo estado sino que también decide, independientemente del estado de la bolsa, si añade otra cuenta a la bolsa o saca una cuenta de la bolsa o la deja igual. La bolsa inicia con una cuenta y el autómata continúa operando mientras haya símbolos de entrada y la bolsa no esté vacía. Si se consumen todos los símbolos de la palabra de entrada al mismo tiempo que se vacía la bolsa, entonces se acepta la palabra.10

11. Ejemplo: {anbn | n  1}11ababq1q2q0

12. Autómatas de pilaDesafortunadamente los autómatas de conteo no son suficientemente poderosos para reconocer todos los LLC.En ocasiones se requiere más de un tipo de cuenta o “roca” o en lugar de una “bolsa”.Se utiliza un stack o pila LIFO (Last In First Out) en el cual el orden es importante. La acción que lleva a cabo el autómata sólo es influenciada no sólo por el estado en que se encuentra y por el símbolo que lee, sino también por el tipo de piedra u objeto que se encuentra arriba en la pila.12Cinta deentradaababbaCabezalectoraq0Controlq1qnq2qiq3Pilaq4

13. Definición formalUn autómata de pila (pushdownautomata) es una sexteta(K, , , , s0, F) donde:K es un conjunto no vacío de estados. es el alfabeto de entrada, no vacío. es el alfabeto de la pila, no vacío.s0  K es el estado inicial.F K es el conjunto de estados finales. (K (  {})  (  {}))  (K  *) es la relación de transición.(p, u, )  (q, )   significa que el autómata está en el estado p, lee el símbolo u, saca  de la pila, pasa al estado q e introduce  a la pila.La operación “push” (sólo meter a la pila) se logra tomando  como la palabra vacía. La operación “pop” (sólo sacar de la pila) se logra tomando  como la palabra vacía.Ya que  es una relación y no necesariamente una función, un autómata de pila es no determinista.Una palabra es aceptada por un AP si al “procesarla” completamente, se llega a un estado final y la pila queda vacía. Debido al no-determinismo del autómata es posible que al terminar de procesar la palabra, varios estados estén activos. Es suficiente que uno de estos estados sea final para que la palabra se acepte. L(M) denota al lenguaje formado por las palabras aceptadas por M.13

14. 14u,  / qpRepresentación gráfica de un APLa transición ((p, u, ), (q, )), (p, u, ) = (q, ), se representa gráficamente pory significa que cuando estamos en el estado p, leemos de la palabra de entrada el símbolo u y sacamos del stack el símbolo , entonces pasamos al estado q y ponemos en la pila la cadena .

15. 15a,  / Ab, A / b, A / q0q1EjemploAutómata de pila que acepte {aibi | i  0}K = {q0, q1} = {a, b} = {A}s0 = q0F = {q0, q1}(q0, a, ) = (q0, A)(q0, b, A) = (q1, )(q1, b, A) = (q1, )

16. 16a,  / Ab,  / Bb, B / a, A / c,  / q0q1Ejemplo: palíndromos de longitud imparAutómata de pila que acepte {wcwR | w {a, b}*}. wR es la palabra w al revés, por ejemplo, “anita”R = “atina”.K = {q0, q1} = {a, b, c} = {A, B}s0 = q0F = {q1}(q0, a, ) = (q0, A) (q1, a, A) = (q1, ) (q0, b, ) = (q0, B) (q1, b, B) = (q1, )(q0, c, ) = (q1, )

17. 17a,  / Ab,  / Bb, B / a, A / ,  / q0q1Ejemplo: palíndromos de longitud parAutómata de pila que acepte {wwR | w {a, b}*}. wR es la palabra w al revés, por ejemplo, “anita”R = “atina”.K = {q0, q1} = {a, b} = {A, B}s0 = q0F = {q1}(q0, a, ) = (q0, A) (q1, a, A) = (q1, ) (q0, b, ) = (q0, B) (q1, b, B) = (q1, )(q0, , ) = (q1, )

18. AF  APTodo lenguaje aceptado por un autómata finito es también aceptado por un autómata de pila.Si M = (K, , , s0, F) es un autómata finito, entonces (K, , , ’, s0, F) con = ’ = {((p, u, ), (q, )) | (p, u, q)  }acepta el mismo lenguaje que M.Los lenguajes libres de contexto son aceptados por los autómatas de pila y los lenguajes generados por los autómatas de pila son los lenguajes libres de contexto.18

19. LLC  APSea G = (V,, R, S) una gramática libre de contexto. Entonces el autómata de pila M = ({p, q}, , V, , p, {q}) donde la relación de transición se define de la siguiente manera acepta exactamente el mismo lenguaje que G.1) (p, , ) = (q, S)2) (q, , A) = (q, x) para cada regla A  x R3) (q, , ) = (q, ) para cada  El autómata de pila contiene sólo dos estados. El primero se utiliza sólo en la primera transición por lo que los estados no sirven para “recordar” las características de la palabra de entrada, este “recordatorio” se hace en la pila. Las transiciones tipo 2) lo que hacen es derivar en la pila la palabra de entrada sin consumir ningún carácter de entrada. Las transiciones tipo 3) comparan la palabra en la pila con la palabra de entrada.19

20. EjemploObtener un AP que acepte el lenguaje generado por la gramática libre de contexto cuyas reglas son: S  aSa S  bSb S  cTransiciones del APTipo 1): (p, , ) = (q, S)Tipo 2): (q, , S) = (q, aSa) (q, , S) = (q, bSb) (q, , S) = (q, c)Tipo 3): (q, a, a) = (q, ) (q, b, b) = (q, ) (q, c, c) = (q, )20

21. ...Ejemplo: analizar abcbaEstado Falta leerPilap abcba q abcba Sq abcba aSaq bcba Saq bcba bSbaq cba Sbaq cba cbaq ba baq a aq 21

22. Cerradura de los LLCDadas dos gramáticas G1 = (V1, S1, R1, S1) y G1 = (V2, S2, R2, S2) entonces (se asume, sin perder generalidad, que los símbolos no terminales de G1 y G2 son disjuntos):La gramática libre de contexto que genera L(G1)  L(G2) esG = (V1 V2 {S},S1S2, R1R2 {SS1, SS2}, S)La gramática libre de contexto que genera L(G1) L(G2) esG = (V1 V2 {S},S1S2, R1R2 {SS1S2}, S)La gramática libre de contexto que genera L(G1)*esG = (V1,S1, R1 {S, SS1S1}, S}Si M1 = (K1, 1, 1, 1, s1, F1) y M2 = (K2, 2, 2, 2, s2, F2) son dos autómatas de pila que aceptan los lenguajes L1 y L2, respectivamente, entonces un autómata de pila que acepta el lenguaje L1 L2 esM1  2 = (K1 K2  {s},1  2, 1  2,{((s, , ),(s1, )), (s, , ),(s2, ))}  1  2, s, F1  F2) 22

23. CONCLUSIONEN ESTA EXPOSICION HEMOS APRENDIDO A ENTENDER LO RELACIONADO CON EL TEMA PRINCIPAL DE LENGUAJES LIBRE DE CONTEXTO QUE DENTRO DE ESTA UNIADAD EXPUSIMOS TRES TEMAS APRENDIENDO Y A ANALIZANDO LA FORMA Y LA UTILIZACION DE LOS MISMOS CON EJEMPLOS Y LA INVESTIGACION REALIZADA.23

24. BIBLIOGRAFIAhttp://www.elprisma.com/http://es.wikipedia.org/wiki/Wikipedia:Portada24