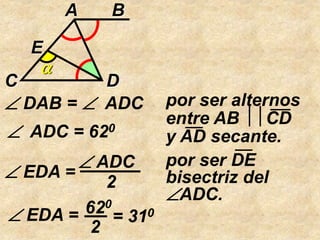
El documento presenta información sobre triángulos, incluyendo definiciones de elementos como vértices, lados y ángulos. También cubre propiedades como la suma de los ángulos interiores, desigualdades triangulares, y puntos y rectas notables como alturas, medianas y bisectrices. Incluye ejemplos de cómo usar esta información para resolver problemas sobre triángulos.

1. Revisión del estudio individual.
x
A E B
D CEn la figura
A = B y
AD || CE.
Probar que:
x = B
A =  B por datos
A =  x por correspondientes
entre AD||CE y AB secante
 x =  B por carácter transitivo
l.q.q.d.

2. Triángulo
Se llama triángulo a la porción del
plano limitada por tres rectas que
se cortan dos a dos.
A B
C
ab
c
 

Elementos:
Vértices: A, B y C
Lados: AB, BC y AC
ó a, b y c
Ángulos:A,B y C
ó ,  y 

3. En todo triángulo se cumple que
cada lado es menor que la suma
de los otros dos y mayor que su
diferencia.
Desigualdad triangular
A
B Ca
bc
En símbolos:
a < b + c
b < a + c
c < a + b
a > b – c
b > a – c
c > a – b
a > b > c

4. Clasificación de los triángulos
según sus lados
Equilátero Isósceles Escaleno
Tiene sus
tres lados
iguales.
A B
C
Tiene dos
lados
iguales.
A B
C
Tiene sus
tres lados
desiguales.
A B
C

5. Clasificación
de los
triángulos
según sus
ángulos
Acutángulo
RectánguloObtusángulo
Tiene sus tres
ángulos agudos.
Uno de sus
ángulos es recto.
Uno de sus
ángulos es
obtuso.

6. Ángulos interiores
En todo triángulo, la suma de los
ángulos interiores es igual a 1800.
A B
C
 

En símbolos:
 +  +  = 1800




7. Ángulos exteriores
Los ángulos exteriores de un
triángulo son los formados por un
lado y la prolongación de otro de
los lados.
A B
C
 


Propiedad:
 =  + 

8. Rectas y puntos
notables del
triángulo

9. ALTURA: es el segmento de
perpendicular trazado desde un
vértice de un triángulo al lado
opuesto.
A B
C
ab
c
hc hc  AB

10. En todo triángulo existen tres alturas
que se intersecan en un punto
llamado ORTOCENTRO.

11. MEDIANA: es el segmento trazado
desde cada vértice de un triángulo
hasta el punto medio del lado
opuesto.
A B
C
ab
c
D
D: punto medio
de AB

12. En todo triángulo existen tres
medianas que se intersecan en
un punto llamado BARICENTRO.

13. BISECTRIZ: es el segmento de bisectriz
de un ángulo interior de un triángulo
determinado por un vértice y el punto
en que la misma corta al lado opuesto.
A B
C
a
b
c D
CD: bisectriz del ACB

14. En todo triángulo existen tres
bisectrices que se intersecan en
un punto llamado INCENTRO.

15. MEDIATRIZ: es la
recta perpendicular en
el punto medio de
cada lado de un
triángulo.
A B
C
ab
c D
r
r  AB
D: punto medio del AB

16. En todo triángulo existen tres
mediatrices que se intersecan en un
punto llamado CIRCUNCENTRO.

17. Recta notable Intersección Propiedad
Altura Ortocentro
Medianas Baricentro
Centro de
gravedad
Bisectriz Incentro
Centro cir.
inscrita
Mediatriz Circuncentro
Centro cir.
circunscrita

18. Ejercicio 1
Determina si se puede construir
un triángulo con tres segmentos
que midan respectivamente:
a) 5; 12 y 4 cm.
b) 23; 36 y 50 cm.
c) 21,4; 8,13 y 7 cm.
No; 12 > 5 + 4
Si; 50 < 23 + 36
No; 21,4 > 8,13 + 7

19. Ejercicio 2

A B
C D
E
En la figura AB││CD;  DAB= 620;
DE: bisectriz del ADC;
AD: bisectriz del CAB. Calcula 

20.  DAB =  ADC por ser alternos
entre AB CD
y AD secante. ADC = 620
 EDA =
 ADC
2
por ser DE
bisectriz del
ADC.
 EDA = 620
2
= 310

A B
C D
E

21. En  EAD tenemos:
 =  CAD +  ADE por ser exterior
al  EAD.
 = 620 +310
 = 930
 CAD =  DAB
por ser AD bisectriz
del CAB.
 CAD = 620

A B
C D
E

22. Para el estudio individual
1.En la figura:
ED  BC;  = 500;
 = 300 y ; CA y
ED se cortan en
F. Halla  y . D A B
C
F
E


