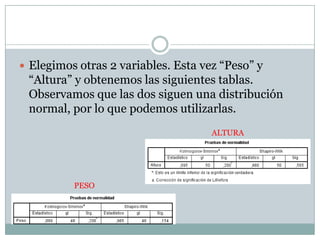
Este documento describe los pasos para realizar un estudio de correlación entre variables cuantitativas. Primero se comprueba si las variables siguen una distribución normal mediante las pruebas de Shapiro-Wilk y Kolmogorov-Smirnov. Luego se eligen las variables "Peso" y "Altura", que siguen una distribución normal, y se calcula su correlación de Pearson, obteniendo una correlación fuerte positiva. Finalmente, se representa gráficamente la relación entre estas variables.

1. J U L I A L E D E S M A G A R C Í A
1 º E N F E R M E R Í A – V I R G E N M A C A R E N A
G R U P O A . S U B G R U P O 3
CORRELACIÓN

2.  Para poder hacer este estudio de correlaciones,
debemos elegir 2 variables cuantitativas pero antes
tenemos que comprobar que siguen la distribución
normal. En este caso hemos elegido “Año de
nacimiento” y “Número de cigarrillos al día”.
 Para hacer dicha comprobación, tenemos que seguir
los siguientes pasos:

5.  Como resultado obtenemos la siguiente tabla, la
cual nos muestra que el nivel de significación (sig.)
es menor de 0,05, por lo que no se podría utilizar
para el estudio.

6.  En la otra variable que hemos elegido (número de
cigarrillos) hacemos el mismo proceso y obtenemos la
siguiente tabla.
 Como podemos ver, el tamaño muestral (gl) es inferior a 50,
por lo que nos fijaríamos en la parte de “Shapiro-Wilk”.
Observamos esa parte de la tabla y comprendemos que el
nivel de significación es menor de 0,05 por lo que tampoco
podría utilizarse esta variable.

7.  Elegimos otras 2 variables. Esta vez “Peso” y
“Altura” y obtenemos las siguientes tablas.
Observamos que las dos siguen una distribución
normal, por lo que podemos utilizarlas.
PESO
ALTURA

8.  PESO: al ser el tamaño muestral (gl) inferior a 50,
observamos el nivel de significación de “Shapiro-
Wilk” y vemos que es mayor de 0,05 por lo que se
podría utilizar.

9.  ALTURA: Al ser el tamaño muestral (gl) igual que
50, observamos que los niveles de significación son
mayores de 0,05 por lo que es posible utilizar esta
variable.

10.  A continuación, comprobamos la correlación entre
estas 2 variables siguiendo los siguientes pasos:
Analizar  Correlaciones  Bivariadas  Elegimos
las dos variables  Seleccionamos Pearson 
Aceptar.

13.  Como resultado, obtenemos la siguiente tabla y
observamos los dos asteriscos que nos informan de la
existencia de una correlación fuerte entre ambas
variables.

14.  Finalmente vamos a representarla gráficamente.
 Seguimos los siguientes pasos:
Gráficos  Cuadros de diálogo antiguos 
dispersión/puntos  Dispersión simple  Definir 
Elegimos variables  Aceptar

18.  Como podemos observar, existe una relación
positiva moderada entre estas variables,
pues cuando cambia de valor una variable,
también lo hace la otra y es positiva porque
el cambio se produce en las dos en la misma
dirección.