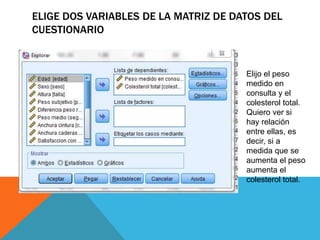
El documento analiza la relación entre dos pares de variables tomadas de un cuestionario: peso y colesterol total, edad y tensión arterial sistólica. Para el primer par, se determina que siguen una distribución normal y no existe correlación entre ellas. Para el segundo par, no siguen una distribución normal pero sí existe una fuerte correlación positiva entre la edad y la tensión arterial.

2. ELIGE DOS VARIABLES DE LA MATRIZ DE DATOS DEL
CUESTIONARIO
Elijo el peso
medido en
consulta y el
colesterol total.
Quiero ver si
hay relación
entre ellas, es
decir, si a
medida que se
aumenta el peso
aumenta el
colesterol total.

3. Primero hacemos la
prueba de normalidad
para cada una de ellas
para ver si son
normales o no.
Seleccionamos
histograma y gráficos
de normalidad con
pruebas.

4. Como el grado de libertad (tamaño muestral) es
mayor de 50 cogemos la prueba de Kolmogorov-
Smirnov. Vemos que p es mayor de 0’05 por lo que
aceptamos la hipótesis nula, y establecemos que las
dos variables siguen una regla de normalidad.

5. Lo podemos ver en
estos gráficos, que
sigue una regla de
normalidad

6. Como ambas variables siguen una regla de normalidad,
utilizamos el coeficiente de Pearson y nos muestra esta tabla.
En ella observamos que la correlación es de 0’164, está cerca
del cero y además vemos que P es mayor de 0’05 por lo que
aceptamos la hipótesis nula, y establecemos que no hay
correlación

7. Al
representarlo
gráficamente
vemos que
hay una nube
de dispersión,
por lo que no
hay
correlación

8. A continuación lo hacemos con otras dos
variables. La edad y la tensión arterial
sistólica, para ver si a medida que la edad
aumenta la tensión arterial sistólica también.

9. Hacemos la prueba de
normalidad de ambas
variables para ver si siguen
una regla de normalidad
Cogemos la prueba de
Kolmogorov ya que el tamaño
muestral es superior a 50. A
continuación vemos que P es
menor de 0’05 por lo que
rechazamos la hipótesis nula y
establecemos que no siguen
una regla de normalidad.

10. En los histogramas de cada variable
podemos corroborar que no siguen
una regla de normalidad

11. Como ambas variables no siguen un criterio de
normalidad, realizamos el coeficiente de
Spearman y observamos que es 0’545. P es 0’00
por lo que al ser menor de 0’05 rechazamos la
Hipótesis nula (h0) y decimos que sí existe
correlación y como el coeficiente está cerca de
1, existe una correlación fuerte.

12. Representaremos la correlación
de las variables gráficamente.
Para ello seleccionamos la
variable independiente y la
situamos en el eje X en este
caso la edad y la variable
dependiente en el eje Y que será
tensión arterial sistólica.

13. Aquí lo tenemos representado y podemos ver que aunque no es perfecta,
podríamos trazar una recta imaginaria