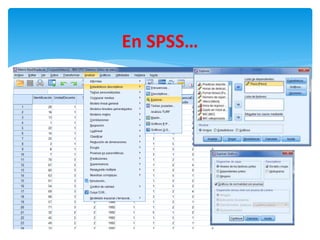
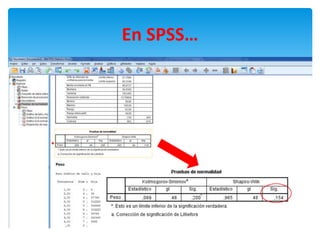
Este documento describe los pasos para analizar la relación entre dos variables utilizando la prueba T de Student. Se realizó un estudio sobre la relación entre el sexo y la práctica de deporte en una muestra. Primero, se sometió la variable del peso a una prueba de normalidad para determinar si seguía una distribución normal. Luego, al obtener un resultado significativo en la prueba T de Student, se concluyó que sí existe una relación entre el sexo y la práctica de deporte en la muestra.

1. Estudio de la relación
entre dos variables.
Prueba T de Student
TICs
Tecnologías de la Información y la
Comunicación

2.  Para analizar si existe relación entre dos variables,
utilizamos la ESTADÍSTICA INFERENCIAL.
 En nuestro ejemplo tenemos una muestra Bivariable:
- Sexo: Variable cualitativa nominal dicotómica
- Peso: Variable cuantitativa continua
¿Tiene relación el peso con
practicar deporte?

3.  Lo primero que debemos hacer es someter a las variables a
la prueba de normalidad. De este modo sabremos si las
variables siguen una distribución normal o no. Debemos
tener en cuenta que las pruebas de normalidad se realizan
solo en variables cuantitativas, por lo la variable del peso a la
prueba de normalidad.
 La distribución normal es aquella representada por la
campana de Gauss. Esta curva, la cual es simétrica, tiene la
peculiaridad de que tanto la media como la mediana y la
moda, coinciden en un mismo punto.
Prueba de normalidad

4.  Para comprobar la normalidad, se utilizan dos tipos de pruebas:
- Prueba de Kolmogorov: se realiza en muestras grandes (N mayor de 50)
- Prueba de Shapiro: se realiza en muestras pequeñas (N menor de 50)
 En este caso, la muestra es justo de 50, por lo que podremos utilizar una
prueba u otra. En este caso, hemos elegido aleatoriamente utilizar la de
Shapiro.
 Elaboramos nuestra hipótesis nula (H0) y nuestra hipótesis alternativa (H1)
- H0: SÍ sigue una distribución normal
- H1: NO sigue una distribución normal
Planteamiento de la prueba de
normalidad

5. En SPSS…

6. Resultados obtenidos en la prueba
de normalidad
 Una vez obtenido el resultado, debemos decidir entre:
- Rechazar la hipótesis nula, si el nivel de significación es menor
de 0,05, dando lugar al a aceptación de la hipótesis alternativa.
- Aceptar la hipótesis nula, si el nivel de significación es mayor de
0,05.
 Resultado obtenido: 0,155 > 0,05, por lo que aceptaremos la
hipótesis nula. La muestra sigue una distribución normal.

7. En SPSS…

8.  Cuando las muestras siguen una distribución normal se aplican las
pruebas paramétricas. En caso de que no siguieran una
distribución normal, se aplicarían las no paramétricas.
 Entre las pruebas paramétricas más utilizadas en enfermería,
escogeremos la T de Student, ya que esta es la que se utiliza para el
análisis bivariado (2 variables). Ahora nuestras hipótesis nula y
alternativa son:
- H0: no existe relación entre el sexo y la práctica de deporte.
- H1: sí existe relación entre el sexo y la práctica de deporte.
Elección de la prueba T de Student
(prueba paramétrica)

9.  Antes de realizar la prueba T de Student, debemos
realizar el test de las varianzas mediante la Prueba de
Levene. Así pues:
- H0: las varianzas son iguales
- H1: las varianzas no son iguales, son distintas.
 Resultado obtenido: 0,096 > 0,05. Por lo tanto, se
asumen que las varianzas son iguales.
Prueba de Levene

10. En SPSS…

11. Resultados obtenidos en la prueba
de T de Student

12.  De nuevo volvemos a los resultados obtenidos en la prueba T
de Student y nos fijamos en el nivel de significación bilateral.
 Resultado obtenido: 0,036 < 0,05. Se rechaza la H0 y se
acepta la H1: sí existe relación entre el sexo y la práctica de
deporte.
 Solución final: Sí existe relación entre el sexo y la práctica de
deporte.
Interpretación de los resultados
obtenidos