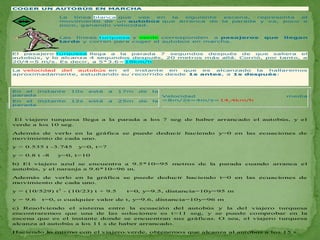
Este documento presenta las aplicaciones de las derivadas en la física. Brevemente explica que la derivada mide la tasa de cambio de una cantidad y puede usarse para calcular la velocidad de un móvil, así como resolver otros problemas físicos donde se requiere medir cómo cambia rápidamente una magnitud. Proporciona ejemplos como calcular la velocidad de crecimiento de bacterias en un cultivo y estimar la velocidad de un autobús.

1. UNIVERSIDAD TECNICA DE MANABI
FACULTAD CIENCIAS INFORMATICA
CARRERA INGIENERIA EN SISTEMAS
Aplicaciones de las Derivadas en la Ciencia
Física
•INTEGRANTES:
•ANGEL ANTONIO MIELES SEGURA
•ROQUE IVAN MACIAS ESPINOZA
•MARIA AUXILIADORA VELEZ MENDOZA
PROF: ING. JOSE
CEVALLOS SALAZAR
SEGUNDO SEMESTRE “C”
ABRIL 2012-SEP.2012

2. Aplicaciones de las
Derivadas en la Ciencia
Física

3. conocida su ley de Movimiento
como también a la solución de
INTRODUCCION La derivada es un concepto que
otros problemas ligados a
tiene variadas aplicaciones.
economía, demografía, Costos,
ingeniería
La derivada expresa la variación
En el Cálculo Diferencial es Se aplica en aquellos casos donde
de las funciones entre dos puntos
fundamental comprender esta es necesario medir la rapidez con
muy cercanos y se Aplica a
idea de incremento que se Asocia que se produce el cambio de
situaciones físicas como el cálculo
a la noción de derivada una magnitud o situación.
de la velocidad de un móvil
. Con esta interpretación, pueden
determinar la ecuación de rectas
y ha permitido a lo largo de los determinarse muchas
tangentes a una curva y calcular
siglos hallar soluciones a propiedades geométricas de los
los valores Máximos o mínimos de
Problemas gráficos de funciones, tales
las funciones.
como concavidad o convexidad.

6. FUNDAMENTACION
Se podrida decir que en la
En física, las física, como en
derivadas se matemática, al decir que la
La Derivada en la velocidad es la DERIVADA
aplican en aquellos física es la pendiente de la posición estamos
casos donde es de la recta tangente tomando un cociente de
necesario medir la geométrica a una curva incrementos
rapidez con que se representativa de una infinitesimales que
produce el cambio función en un cierto representan o se
punto interpretan como la
de una magnitud o pendiente de la función de
situación posición a lo largo del
tiempo.

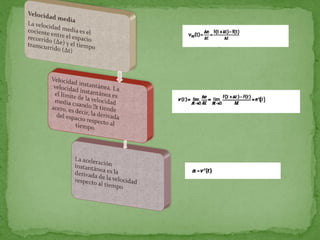
8. La velocidad instantánea en t = 1.
La velocidad instantánea es la derivada en t = 1.
Ejemplo de tiempo
Imaginemos que el número de bacterias de un cultivo varía con el tiempo,
expresado en minutos, según la ecuación N=500+50t-t2 para t[0,35]
¿Cuál es la velocidad de crecimiento de la población en el instante t=7
min?
Hallando la derivada de la función N(t), N'(t) es la velocidad de crecimiento de la
población en cualquier instante t.

9. COGER UN AUTOBÚS EN MARCHA
La línea blanca que ves en la siguiente escena, representa el
movimiento de un autobús que arranca de la parada y va, poco a
poco, ganando velocidad.
Las líneas turquesa y verde corresponden a pasajeros que llegan
tarde y corren para coger el autobús en marcha.
El pasajero turquesa llega a la parada 7 segundos después de que saliera el
autobús, y lo alcanza 4 segundos después, 20 metros más allá. Corrió, por tanto, a
20/4=5 m/s. Es decir, a 5*3.6=18km/h
La velocidad del autobús en el instante en que es alcanzado la hallaremos
aproximadamente, estudiando su recorrido desde 1s antes, a 1s después:
En el instante 10s está a 17m de la
parada Velocidad media
En el instante 12s está a 25m de la =8m/2s=4m/s=14,4km/h
parada
El viajero turquesa llega a la parada a los 7 seg de haber arrancado el autobús, y el
verde a los 10 seg.
Además de verlo en la gráfica se puede deducir haciendo y=0 en las ecuaciones de
movimiento de cada uno.
y = 0.535 t -3.745 y=0, t=7
y = 0.8 t -8 y=0, t=10
b) El viajero azul se encuentra a 9.5*10=95 metros de la parada cuando arranca el
autobús, y el naranja a 9.6*10=96 m.
Además de verlo en la gráfica se puede deducir haciendo t=0 en las ecuaciones de
movimiento de cada uno.
y = (10/529) t2 - (10/23) t + 9.5 t=0, y=9.5, distancia=10y=95 m
y = 9.6 t=0, o cualquier valor de t, y=9.6, distancia=10y=96 m
c) Resolviendo el sistema entre la ecuación del autobús y la del viajero turquesa
encontraremos que una de las soluciones es t=11 seg, y se puede comprobar en la
escena que es el instante donde se encuentran sus gráficas. O sea, el viajero turquesa
alcanza al autobús a los 11 s de haber arrancado.
Haciendo lo mismo con el viajero verde, obtenemos que alcanza al autobús a los 15 s.

10. Bibliografía:
http://www.slideshare.net/kettyunac/la-derivada-1732683
http://es.scribd.com/doc/56214826/Aplicaciones-de-las-Derivadas-en-Fisica
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Derivadas_aplicaciones_opti
mizacion/pag7.htm