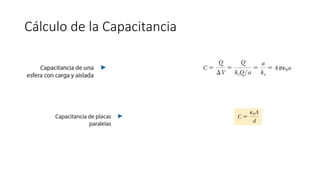
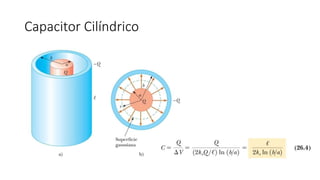
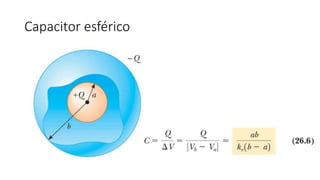
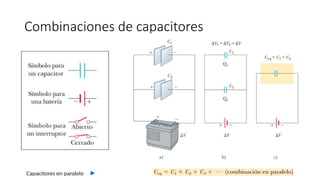
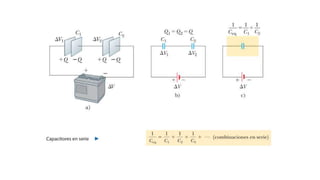
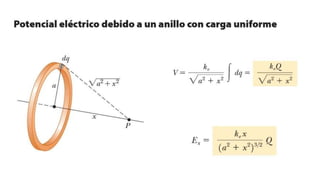
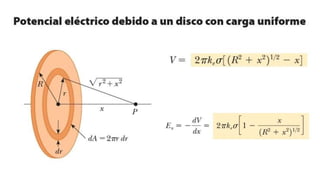
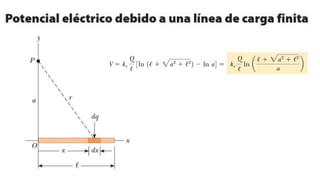
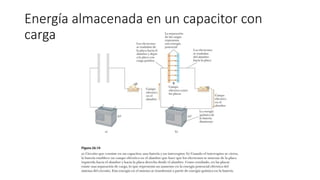
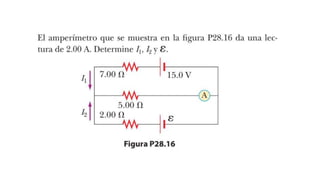
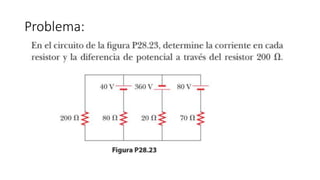
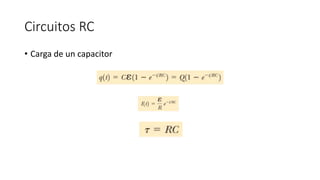
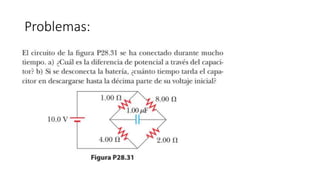
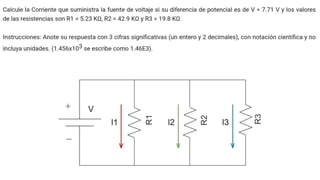
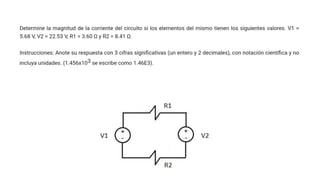
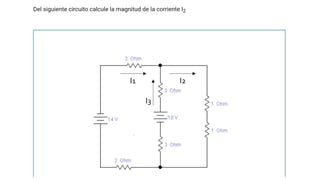
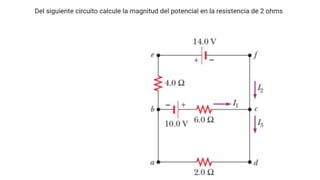
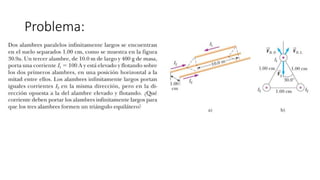
El documento aborda conceptos fundamentales de capacitancia, incluyendo su cálculo y la influencia de materiales dieléctricos en su comportamiento, así como la diferencia entre potencial eléctrico y energía potencial. Se presentan fórmulas específicas para determinar la capacitancia de capacitores cilíndricos y esféricos, y se incluyen problemas prácticos relacionados con circuitos eléctricos, resistencia y conductividad. Se enfatiza la importancia del punto de referencia y la geometría del objeto en la medición de la capacitancia.

1. Capacitancia y Materiales
Dieléctricos

2. Capacitancia

3. Cálculo de la Capacitancia

4. Capacitor Cilíndrico

5. Capacitor esférico

6. Problemas para entregar:

7. Problemas:

8. Combinaciones de capacitores

10. Problemas para entregar, (Asistencia):

16. Colegiada 1

19. Energía almacenada en un capacitor con
carga

21. Densidad de energía

22. Problema:

23. Capacitores con material dieléctrico
• Un dieléctrico es un material no conductor, como el hule, el vidrio o el
papel encerado.
• El factor adimensional k se llama constante dieléctrica del material. La
constante dieléctrica varía de un material a otro.

24. Un dieléctrico tiene las siguientes ventajas:
• Incrementa la capacitancia.
• Incrementa el voltaje máximo de operación.
• Proporciona un posible soporte mecánico entre las placas, lo que
permite que estén cerca una de la otra sin tocarse, así reduce d y
aumenta C.

25. Corriente Eléctrica
• La corriente es la proporción a la cual circula la carga a través de una
superficie
• Corriente instantánea

26. • Es una regla convencional asignar a la corriente la misma dirección
que la del flujo de la carga positiva. En los conductores eléctricos,
como cobre o aluminio, la corriente está ocasionada por el
movimiento de electrones con carga negativa. Por lo tanto, en
cualquier conductor, la dirección de la corriente es la opuesta a la
dirección del flujo de los electrones.
Modelo microscópico de la corriente

27. Problema:

28. Resistencia

30. Problema:

31. Modelo de conducción eléctrica

32. Resistencia y Temperatura

33. Potencia eléctrica

35. Problema:

36. Problemas:

37. Circuitos RC
• Carga de un capacitor

38. Descarga de un capacitor

39. Problemas:

40. Problemas

41. Resumen:
• El potencial eléctrico es una medida de la energía potencial eléctrica
por unidad de carga eléctrica en un punto en el espacio. Se
representa por la letra V y se mide en voltios (V).
• La fórmula para calcular el potencial eléctrico V en un punto P
debido a una carga puntual q en un punto O se puede expresar
como:
V = k * q / r
• La principal diferencia entre el potencial eléctrico y la energía
potencial es que el potencial eléctrico es una propiedad por unidad
de carga eléctrica, mientras que la energía potencial es una
propiedad total asociada con una carga en un campo eléctrico.

42. • Para calcular la energía potencial eléctrica asociada con una
carga en un campo eléctrico, se puede utilizar la siguiente
fórmula:
U = qV
• Es importante tener en cuenta que la energía potencial eléctrica
es una cantidad relativa, es decir, la energía potencial eléctrica
de una carga en un punto dado depende del punto de
referencia que se utilice para medir el potencial eléctrico. Por lo
tanto, al calcular la energía potencial eléctrica, se debe tener en
cuenta el punto de referencia elegido.

43. Problema general:

44. Resumen: Capacitancia
• La capacitancia es una propiedad eléctrica que mide la capacidad de un
objeto para almacenar carga eléctrica en un campo eléctrico. Es una
medida de la cantidad de carga eléctrica que puede almacenar un objeto a
una diferencia de potencial (voltaje) dado. La capacitancia se mide en
unidades de Faradios (F).
• La capacitancia se define matemáticamente como la relación entre la carga
eléctrica almacenada en un objeto y la diferencia de potencial (voltaje)
entre las dos placas del objeto. Matemáticamente, se puede escribir como:
C = Q / V
• donde C es la capacitancia en Faradios, Q es la carga almacenada en el
objeto en Coulombs, y V es la diferencia de potencial entre las dos placas
del objeto en Voltios.

45. • La capacitancia depende de varios factores, entre los que se incluyen
la geometría del objeto, el material del que está hecho el objeto y la
distancia entre las dos placas del objeto. Por ejemplo, la capacitancia
de un capacitor de placas paralelas depende de la distancia entre las
placas, el área de las placas y la permitividad del material entre las
placas.
• Para calcular la capacitancia de un capacitor de placas paralelas, se
utiliza la siguiente fórmula:
C = ε * A / d

46. • Para calcular la capacitancia de un capacitor cilíndrico, podemos
utilizar la siguiente fórmula:
C = (2 * π * ε * L) / ln(b/a)
donde C es la capacitancia en Faradios, ε es la permitividad del medio
entre los cilindros, L es la longitud del capacitor, a es el radio del
cilindro interno y b es el radio del cilindro externo.
• Esta fórmula es válida para un capacitor de dos cilindros coaxiales, es
decir, dos cilindros uno dentro del otro, separados por un dieléctrico.
El cilindro interno se considera el conductor positivo y el cilindro
externo se considera el conductor negativo.

47. • Para calcular la capacitancia de un capacitor esférico, podemos
utilizar la siguiente fórmula:
C = 4πε₀ (a b) / (b-a)
• donde C es la capacitancia en Faradios, ε₀ es la permitividad del vacío,
a es el radio del conductor interno (positivo) y b es el radio del
conductor externo (negativo).

48. Problemas:
1. Un capacitor de placas paralelas tiene una
separación de 1 cm entre las placas y un área de 0.1
m². Las placas están cargadas con una carga de 5
microculombios. Calcule la capacitancia del
capacitor y la diferencia de potencial entre las
placas.
2. Un capacitor está compuesto por dos cilindros
coaxiales de radio interior “0.02 m" y radio exterior
“0.05 m". Entre los cilindros se encuentra un
dieléctrico con una constante dieléctrica relativa de
2. Si la longitud del capacitor es de 10 cm, determina
la capacitancia del mismo.
3. Cuatro capacitores están conectados como se muestra en
la figura. a) Encuentre la capacitancia equivalente entre
los puntos a y b. b) Calcule la carga de cada uno de los

49. Problemas: Conductividad y Resistividad
• En un tubo de rayos catódicos la intensidad de corriente
eléctrica del haz de partículas de 7.7 μA constantes. Calcular el
número de electrones que entra por la pantalla del tubo cada
18.29 μs.
• Se tienen 4 resistencias en serie y cada una tiene un valor de
3.52 kΩ, a estas se les coloca en serie un conjunto de 3
resistencias conectadas en paralelo, estas 3 resistencias en
paralelo cada una tiene un valor de 3.51 kΩ. Calcule la
resistencia equivalente de dicho arreglo.
• Un primer conductor cilíndrico presenta una resistencia
eléctrica de 1.63 kΩ. Determinar la resistencia de otro
conductor del mismo material que tiene 1.40 veces la
longitud del primer conductor y la mitad de la sección
transversal.

50. Problemas: Leyes de kirchhoff

56. Movimiento de una partícula con carga en un
campo magnético uniforme

60. Problemas:

61. Problema:

62. Problema: