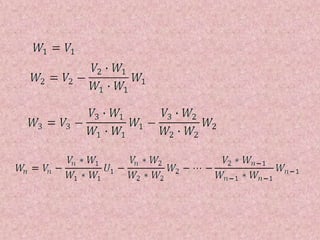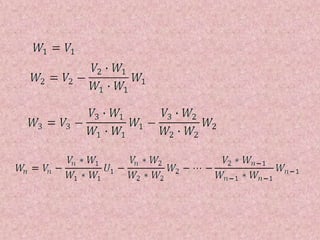
El proceso de Gram-Schmidt permite obtener una base ortogonal y luego ortonormal para cualquier subespacio vectorial W de un espacio vectorial V con producto interno. Primero se toma cualquier base S de V y se aplica el proceso de Gram-Schmidt para obtener una base ortogonal W. Luego, cada vector de W se normaliza para obtener una base ortonormal B''.

1. Proceso de Gram-SchmidtSea (V,K,+,*) un espacio vectorial definido con producto interno, W es subespacio vectorial de V. DimV=n, entonces W tiene una base ortonormal.

2. Todo subespacio V con producto punto tiene al menos una base ortogonal y una base ortonormal. Si S = {v1, . . . , vn} es cualquier base de V , entonces W= {W1, . . . , Wn} es una base ortogonal, donde:

4. Y Gen{v1, . . . , vi} = Gen{W1, . . . , Wi},i = 1, . . . , nUna base ortonormal B′′ se obtiene normalizando B′.