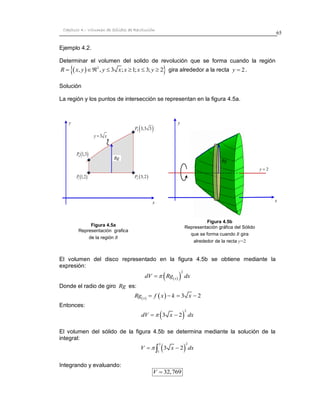
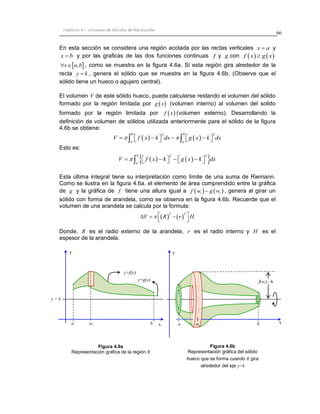
1) El documento describe el cálculo del volumen de sólidos de revolución mediante el método del disco. 2) Explica cómo determinar el volumen sumando los volúmenes de cilindros circulares rectos de corta altura (discos) que forman el sólido al girar una región plana alrededor de un eje. 3) También cubre cómo calcular el volumen cuando la región gira alrededor de un eje paralelo al eje x pero distinto, así como el cálculo para sólidos huecos.