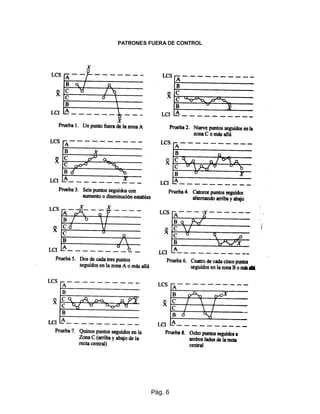
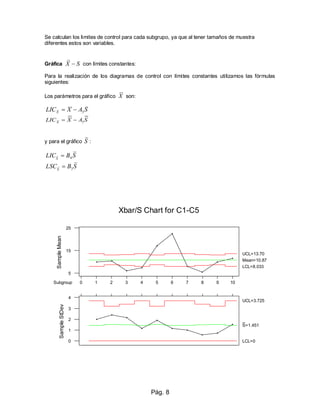
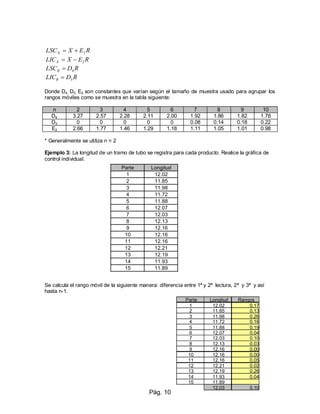
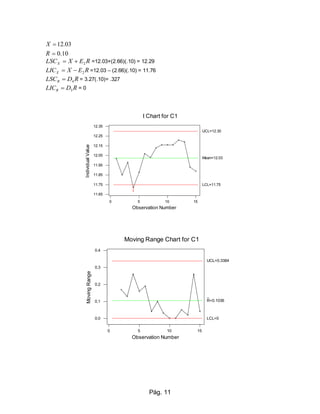
El documento describe las cartas de control, que son herramientas estadísticas para analizar la variación en procesos. Explica cómo construir cartas de control para variables (RX y SX) y atributos, y cómo interpretar los resultados para identificar causas comunes y especiales de variación y determinar si un proceso está bajo control estadístico. Proporciona un ejemplo detallado de cómo construir una carta de control RX para medir el diámetro de una pieza cilíndrica.

1. Pág. 1
CARTAS DE CONTROL
Las cartas de control son la herramienta más poderosa para analizar la variación en la mayoría de
los procesos.
Han sido difundidas exitosamente en varios países dentro de una amplia variedad de situaciones
para el control del proceso.
Las cartas de control enfocan la atención hacia las causas especiales de variación cuando estas
aparecen y reflejan la magnitud de la variación debida a las causas comunes.
Las causas comunes o aleatorias se deben a la variación natural del proceso.
Las causas especiales o atribuibles son por ejemplo: un mal ajuste de máquina, errores del
operador, defectos en materias primas.
Se dice que un proceso está bajo Control Estadístico cuando presenta causas comunes
únicamente. Cuando ocurre esto tenemos un proceso estable y predecible.
Cuando existen causas especiales el proceso está fuera de Control Estadístico; las gráficas de
control detectan la existencia de estas causas en el momento en que se dan, lo cual permite que
podamos tomar acciones al momento.
Ventajas:
 Es una herramienta simple y efectiva para lograr un control estadístico.
 El operario puede manejar las cartas en su propia área de trabajo, por lo cual puede dar
información confiable a la gente cercana a la operación en el momento en que se deben de
tomar ciertas acciones.
 Cuando un proceso está en control estadístico puede predecirse su desempeño respecto a las
especificaciones. En consecuencia, tanto el productor como el cliente pueden contar con
niveles consistentes de calidad y ambos pueden contar con costos estables para lograr ese
nivel de calidad.
 Una vez que un proceso se encuentra en control estadístico, su comportamiento puede ser
mejorado posteriormente reduciendo la variación.
 Al distinguir ente las causas especiales y las causas comunes de variación, dan una buena
indicación de cuándo un problema debe ser corregido localmente y cuando se requiere de una
acción en la que deben de participar varios departamentos o niveles de la organización.
Cartas de control por variables y por atributos.-
En Control de Calidad mediante el término variable se designa a cualquier característica de
calidad “medible” tal como una longitud, peso, temperatura, etc. Mientras que se denomina
atributo a las características de calidad que no son medibles y que presentan diferentes estados
tales como conforme y disconforme o defectuoso y no defectuoso.
Según sea el tipo de la característica de calidad a controlar así será el correspondiente Gráfico de
Control que, por tanto, se clasifican en Cartas de Control por Variables y Cartas de Control por
Atributos.

2. Pág. 2
Comparación de las cartas de control por variables vs. atributos
Cartas de Control por variables Cartas de control por atributos
Ventajas significativas Conducen a un mejor
procedimiento de control.
Son potencialmente aplicables
a cualquier proceso
Proporcionan una utilización
máxima de la información
disponible de datos.
Los datos están a menudo
disponibles.
Son rápidos y simples de
obtener.
Son fáciles de interpretar.
Son frecuentemente usados en
los informes a la Gerencia.
Más econónomicas
Desventajas significativas No se entienden a menos que
se de capacitación; puede
causar confusión entre los
limites de especificación y los
límites de tolerancia.
No proporciona información
detallada del control de
características individuales.
No reconoce distintos grados
de defectos en las unidades de
producto.
Campos de aplicación de las cartas
VARIABLES
Carta Descripción Campo de aplicación.
RX  Medias y Rangos Control de características individuales.
SX  Medias y desviación
estándar.
Control de características individuales.
I Individuales Control de un proceso con datos variables que no pueden ser
muestreados en lotes o grupos.
ATRIBUTOS
Carta Descripción Campo de aplicación.
P Proporciones Control de la fracción global de defectuosos de un proceso.
NP Número de
defectuosos
Control del número de piezas defectuosas
C Defectos por unidad Control de número global de defectos por unidad
U Promedio de
defectos por unidad
Control del promedio de defectos por unidad.

3. Pág. 3
Elaboración de Cartas de control RX  (variables)
Paso 1: Colectar los datos.
Los datos son el resultado de la medición de las características del producto, los cuales deben de
ser registrados y agrupados de la siguiente manera:
 Se toma una muestra(subgrupo) de 2 a 10 piezas consecutivas y se anotan los resultados de
la medición( se recomienda tomar 5). También pueden ser tomadas en intervalos de tiempo de
½ - 2 hrs., para detectar si el proceso puede mostrar inconsistencia en breves periodos de
tiempo.
 Se realizan las muestras de 20 a 25 subgrupos.
Paso 2: Calcular el promedio RyX para cada subgrupo
N
XXX
X N....21 

menormayor XXR 
Paso 3: Calcule el rango promedio  R y el promedio del proceso  X .
K
RRR
R K......21 

K
XXX
X K.......21 

Donde K es el número de subgrupos, R1,R2..es el rango de cada subgrupo; ....21, XX son el
promedio de cada subgrupo.
Paso 4: Calcule los limites de control
Los límites de control son calculados para determinar la variación de cada subgrupo, están
basados en el tamaño de los subgrupos y se calculan de la siguiente forma:
RDLSCR 4 RAXLSCX 2
RAXLICX 2
Donde D4, D3, A2 son constantes que varían según el tamaño de muestra. A continuación se
presentan los valores de dichas constantes para tamaños de muestra de 2 a 10.
n 2 3 4 5 6 7 8 9 10
D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
D3 0 0 0 0 0 0.08 0.14 0.18 0.22
A2 1.88 1.02 0.73 0.58 0.48 0.42 0.37 0.34 0.31
RDLICR 3

4. Pág. 4
Paso 5: Seleccione la escala para las gráficas de control
Para la gráfica X la amplitud de valores en la escala debe de ser al menos del tamaño de los
límites de tolerancia especificados o dos veces el rango promedio  R .
Para la gráfica R la amplitud debe extenderse desde un valor cero hasta un valor superior
equivalente a 1½ - 2 veces el rango.
Paso 6: Trace la gráfica de control
Dibuje las líneas de promedios y límites de control en las gráficas.
Los límites de Control se dibujan con una línea discontinua y los promedios con una línea continua
para ambas gráficas.
Marcar los puntos en ambas gráficas y unirlos para visualizar de mejor manera el comportamiento
del proceso.
Paso 7: Analice la gráfica de control
Ejemplo 1
Se toman las medidas de los diámetros de una pieza cilíndrica, el tamaño de muestra de cada
subgrupo es de cinco, y se toman 25 subgrupos a intervalos de 1 hr.
Realice la carta de control RX  .
Calculando el rango y el promedio para cada subgrupo obtenemos:
Calculando el Rango promedio, promedio del proceso y límites de control:
muestra subgrupo 1 2 3 4 5 6 7 8 9 10 11 12 13
1 0.65 0.75 0.75 0.60 0.70 0.60 0.15 0.60 0.65 0.60 0.80 0.85 0.70
2 0.70 0.85 0.80 0.70 0.75 0.75 0.80 0.70 0.80 0.70 0.75 0.75 0.70
3 0.65 0.75 0.80 0.70 0.65 0.75 0.65 0.80 0.85 0.60 0.90 0.85 0.75
4 0.65 0.85 0.70 0.75 0.85 0.85 0.75 0.75 0.85 0.80 0.50 0.65 0.75
5 0.85 0.65 0.75 0.65 0.80 0.70 0.70 0.75 0.75 0.65 0.80 0.70 0.70
muestra subgrupo 14 15 16 17 18 19 20 21 22 23 24 25
1 0.65 0.90 0.75 0.75 0.75 0.65 0.60 0.50 0.60 0.80 0.65 0.65
2 0.70 0.80 0.80 0.70 0.70 0.65 0.60 0.55 0.80 0.65 0.60 0.70
3 0.85 0.80 0.75 0.85 0.60 0.85 0.65 0.65 0.65 0.75 0.65 0.70
4 0.75 0.75 0.80 0.70 0.70 0.65 0.60 0.80 0.65 0.65 0.60 0.60
5 0.60 0.85 0.65 0.80 0.60 0.70 0.65 0.80 0.75 0.65 0.70 0.65
muestra subgrupo 1 2 3 4 5 6 7 8 9 10 11 12 13
1 0.65 0.75 0.75 0.60 0.70 0.60 0.15 0.60 0.65 0.60 0.80 0.85 0.70
2 0.70 0.85 0.80 0.70 0.75 0.75 0.80 0.70 0.80 0.70 0.75 0.75 0.70
3 0.65 0.75 0.80 0.70 0.65 0.75 0.65 0.80 0.85 0.60 0.90 0.85 0.75
4 0.65 0.85 0.70 0.75 0.85 0.85 0.75 0.75 0.85 0.80 0.50 0.65 0.75
5 0.85 0.65 0.75 0.65 0.80 0.70 0.70 0.75 0.75 0.65 0.80 0.70 0.70
Promedio 0.70 0.77 0.76 0.68 0.75 0.73 0.61 0.72 0.78 0.67 0.75 0.76 0.72
Rango 0.20 0.20 0.10 0.15 0.20 0.25 0.65 0.20 0.20 0.20 0.40 0.20 0.05
muestra subgrupo 14 15 16 17 18 19 20 21 22 23 24 25
1 0.65 0.90 0.75 0.75 0.75 0.65 0.60 0.50 0.60 0.80 0.65 0.65
2 0.70 0.80 0.80 0.70 0.70 0.65 0.60 0.55 0.80 0.65 0.60 0.70
3 0.85 0.80 0.75 0.85 0.60 0.85 0.65 0.65 0.65 0.75 0.65 0.70
4 0.75 0.75 0.80 0.70 0.70 0.65 0.60 0.80 0.65 0.65 0.60 0.60
5 0.60 0.85 0.65 0.80 0.60 0.70 0.65 0.80 0.75 0.65 0.70 0.65
Promedio 0.71 0.82 0.75 0.76 0.67 0.70 0.62 0.66 0.69 0.70 0.64 0.66
Rango 0.25 0.15 0.15 0.15 0.15 0.20 0.05 0.30 0.20 0.15 0.10 0.10

5. Pág. 5
198.R
X = .71
RDLSCR 4 = 2.11* 0.198 = 0.41
= 0
RAXLSCX 2 = .71+(.58)(.198) = .82
RAXLICX 2 = .71-(.58)(.198) = .59
La carta de control R muestra un punto fuera de los limites de especificaciones, por lo cual el
proceso se encuentra fuera de control, en este caso es necesario investigar las causas y tomar las
acciones correctivas para eliminar el problema. En la siguiente parte se muestran los criterios para
determinar las situaciones en las cuales un proceso puede estar fuera de control.
Interpretación del control del proceso.
El objeto de analizar una gráfica de control es identificar cuál es la variación del proceso, las
causas comunes y causas especiales de dicha variación y en función de esto tomar alguna acción
apropiada cuando se requiera.
Juran1
sugiere un conjunto de reglas de decisión para detectar patrones no aleatorios en las cartas
de control. Cuando se detecta alguno de los patrones siguientes se puede decir que el tomar
alguna acción para corregir el problema ya que el proceso puede estar fuera de control.
1
Análisis y planeación de la calidad, J.M. Juran ,F.M Gryna, Tercera Edición, McGrawHill.
252015105Subgroup 0
0.8
0.7
0.6
SampleMean
Mean=0.7112
UCL=0.8254
LCL=0.5970
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
SampleRange
1
R=0.198
UCL=0.4187
LCL=0
Xbar/R Chart for C1
RDLICR 3

6. Pág. 6
PATRONES FUERA DE CONTROL

7. Pág. 7
Gráficas de control SX  (variables)
El procedimiento para realizar las cartas de control SX  es similar al de las cartas RX  La
diferencia consiste en que el tamaño de la muestra puede variar y es mucho más sensible para
detectar cambios en la media o en la variabilidad del proceso.
El tamaño de muestra n es mayor a 9.La Carta X monitorea el promedio del proceso para vigilar
tendencias.
La Carta S monitorea la variación en forma de desviación estándar.
Terminología
k = número de subgrupos
n = número de muestras en cada subgrupo
X = promedio para un subgrupo
X = promedio de todos los promedios de los subgrupos
S = Desviación estándar de un subgrupo
S

= Desviación est. promedio de todos los subgrupos
N
XXX
X N....21 

K
XXX
X K.......21 

SAXLSCX 3
SAXLICX 3
SBLSCS 4
SBLICS 3
Ejemplo 2
Se registra el peso diariamente durante dos semanas. Realizar la gráfica de control SX 
88.10X
46.1S
Día Muestra1 Muestra2 Muestra3 Muestra4 Muestra5 S
1 10 12 8 10.00 2.00
2 12 11 7 9 13 10.40 2.41
3 5 6 4 9 6.00 2.16
4 8 8 6 7.33 1.15
5 17 15 16 18 20 17.20 1.92
6 22 24 22 22.67 1.15
7 8 9 7 8.00 1.00
8 6 5 6 5 5.50 0.58
9 10 10 10 11 9 10.00 0.71
10 13 10 12 11.67 1.53
10.88 1.46
X

8. Pág. 8
Se calculan los limites de control para cada subgrupo, ya que al tener tamaños de muestra
diferentes estos son variables.
Gráfica SX 

con límites constantes:
Para la realización de los diagramas de control con límites constantes utilizamos las fórmulas
siguientes:
Los parámetros para el gráfico X son:
SAXLICX 3
y para el gráfico S :
SBLSC
SBLIC
S
S
3
4


SAXLICX 3
10987654321Subgroup 0
25
15
5
SampleMean
Mean=10.87
UCL=13.70
LCL=8.033
4
3
2
1
0
SampleStDev
S=1.451
UCL=3.725
LCL=0
Xbar/S Chart for C1-C5

9. Pág. 9
Ejemplo 3:
Las siguientes cifras son la medias y las desviaciones estándar de muestras de 5 observaciones
correspondientes a los diámetros de una pieza metálica:
muestra X-bar Si muestra X-bar Si
1 74.01 0.0148 14 73.99 0.0153
2 74.001 0.0072 15 74.006 0.0073
3 74.008 0.0106 16 73.997 0.0078
4 74.003 0.0091 17 74.001 0.0106
5 74.003 0.0122 18 74.007 0.007
6 73.996 0.0087 19 73.998 0.0085
7 74 0.0055 20 74.009 0.008
8 73.997 0.0123 21 74 0.0053
9 74.004 0.0055 22 74.002 0.0074
10 73.998 0.0063 23 74.002 0.0119
11 73.994 0.0029 24 74.005 0.0087
12 74.001 0.0042 25 73.998 0.0162
13 73.998 0.0105 PROMEDIOS 74.001 0.0090
De la tabla tenemos que: 001.74X y S = .0090
Calculamos los limites de control:
SAXLICX 3 = 74.001 + (1.427)(.0090) = 74.014
SAXLICX 3 = 74.001 – (1.427)(.0090) = 73.998
SBLICS 4 = (2.089)(.0090) = 0.019
SBLSCS 3 = (0)(.0090) = 0
Carta de control de lecturas Individuales I-MR (Datos variables).
 A menudo esta carta se llama “I” o “Xi”.
 Esta Carta monitorea la tendencia de un proceso con datos variables que no pueden ser
muestreados en lotes o grupos.
 Este es el caso cuando la capacidad de corto plazo se basa en subgrupos racionales de una
unidad o pieza.
 Este tipo de gráfica es utilizada cuando las mediciones son muy costosas(Ej. Pruebas
destructivas), o cuando la característica a medir en cualquier punto en el tiempo es
relativamente homogénea (Ej. el PH de una solución química)
 La línea central se basa en el promedio de los datos, y los límites de control se basan en la
desviación estándar (+/- 3 sigmas)
Terminología
k = número de piezas
n = 2 para calcular los rangos
X = promedio de los datos
R = rango de un subgrupo de dos piezas consecutivas
R = promedio de los (n - 1) rangos

10. Pág. 10
REXLSCX 2
REXLICX 2
RDLSCR 4
RDLICR 3
Donde D4, D3, E2 son constantes que varían según el tamaño de muestra usado para agrupar los
rangos móviles como se muestra en la tabla siguiente:
n 2 3 4 5 6 7 8 9 10
D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
D3 0 0 0 0 0 0.08 0.14 0.18 0.22
E2 2.66 1.77 1.46 1.29 1.18 1.11 1.05 1.01 0.98
* Generalmente se utiliza n = 2
Ejemplo 3: La longitud de un tramo de tubo se registra para cada producto. Realice la gráfica de
control individual.
Se calcula el rango móvil de la siguiente manera: diferencia entre 1ª y 2ª lectura, 2ª y 3ª y así
hasta n-1.
Parte Longitud
1 12.02
2 11.85
3 11.98
4 11.72
5 11.88
6 12.07
7 12.03
8 12.13
9 12.16
10 12.16
11 12.16
12 12.21
13 12.19
14 11.93
15 11.89
Parte Longitud Rangos
1 12.02 0.17
2 11.85 0.13
3 11.98 0.26
4 11.72 0.16
5 11.88 0.19
6 12.07 0.04
7 12.03 0.10
8 12.13 0.03
9 12.16 0.00
10 12.16 0.00
11 12.16 0.05
12 12.21 0.02
13 12.19 0.26
14 11.93 0.04
15 11.89
12.03 0.10

11. Pág. 11
10.0
03.12


R
X
REXLSCX 2 =12.03+(2.66)(.10) = 12.29
REXLICX 2 =12.03 – (2.66)(.10) = 11.76
RDLSCR 4 = 3.27(.10)= .327
RDLICR 3 = 0
151050
12.35
12.25
12.15
12.05
11.95
11.85
11.75
11.65
Observation Number
IndividualValue
I Chart for C1
1
Mean=12.03
UCL=12.30
LCL=11.75
151050
0.4
0.3
0.2
0.1
0.0
Observation Number
MovingRange
Moving Range Chart for C1
R=0.1036
UCL=0.3384
LCL=0

12. Pág. 12
Interpretación del proceso:
 Revisar la gráfica de rangos para puntos fuera de los límites de control como signo de la
existencia de causas especiales. Note que los rangos sucesivos están correlacionados, debido
a que tienen un punto en común y debido a esto se tiene que tener cuidado al interpretar
tendencias.
 Las gráficas por lecturas individuales pueden ser analizadas para puntos fuera de los límites de
control, dispersión de puntos dentro de los límites de control y para tendencias o patrones.
Cabe hacer notar que si la distribución de proceso no es simétrica, las reglas mostradas
anteriormente para gráficas X podrán dar señales de causas especiales sin que éstas existan.
Gráficas de control por atributos
Cualquier característica de calidad que pueda ser clasificada de forma binaria: “cumple o no
cumple”, “funciona o no funciona”, “pasa o no pasa”, etc., a los efectos de control del proceso, será
considerado como un atributo y para su control se utilizará un Gráfico de Control por Atributos.
:
Los criterios de aceptación al utilizar gráficas de control por atributos deben estar claramente
definidos y el procedimiento para decidir si esos criterios se están alcanzando es producir
resultados consistentes a través del tiempo. Este procedimiento consiste en definir
operacionalmente lo que se desea medir. Una definición operacional consiste en:
1º . Un criterio que se aplica a un objeto o a un grupo
2º. Una prueba del objeto o del grupo y
3º. Una decisión, sí o no: El objeto o el grupo alcanza o no el criterio.
Gráfica P para fracción de Unidades Defectuosas (atributos)
La gráfica p mide la fracción defectuosa o sea las piezas defectuosas en el proceso. Se puede
referir a muestras de 75 piezas, tomada dos veces por día; 100% de la producción durante una
hora, etc. Se basa en la evaluación de una característica (¿se instalo la pieza requerida?) o de
muchas características (¿se encontró algo mal al verificar la instalación eléctrica?). Es importante
que cada componente o producto verificado se registre como aceptable o defectuoso (aunque una
pieza tenga varios defectos específicos se registrará sólo una vez como defectuosa).
Pasos para la elaboración de la gráfica:
Paso 1- Frecuencia y tamaño de la muestra:
Establezca la frecuencia con la cual los datos serán tomados (horaria, diaria, semanal). Los
intervalos cortos entre tomas de muestras permitirán una rápida retroalimentación al proceso ante
la presencia de problemas. Los tamaños de muestra grandes permiten evaluaciones más estables
del desarrollo del proceso y son más sensibles a pequeños cambios en el promedio del mismo. Se
aconseja tomar tamaños de muestra iguales aunque no necesariamente se tiene que dar esta
situación, el tamaño de muestra debería de ser mayor a 30. El tamaño de los subgrupos será de 25
o más.
Paso 2- Calculo del porcentaje defectuoso (p) del subgrupo:
Registre la siguiente información para cada subgrupo:
El número de partes inspeccionadas – n
El número de partes defectuosas – np

13. Pág. 13
Calcule la fracción defectuosa (p) mediante:
n
np
p 
Paso 3 – Calculo de porcentaje defectuoso promedio y límites de control
El porcentaje defectuoso promedio para los k subgrupos se calcula con la siguiente fórmula:
k
k
nnn
npnpnp
p



.....
....
21
21
n
pp
pLSCp
)1(
3


n
pp
pLICp
)1(
3


donde n es el tamaño de muestra promedio.
NOTA: Cuando p y/o n es pequeño, el límite de control inferior puede resultar negativo, en estos
casos el valor del límite será = 0
Paso 4- Trace la gráfica y analice los resultados.
Ejemplo 4
Un fabricante de latas de aluminio registra el número de partes defectuosas, tomando muestras
cada hora de n = 50, con 30 subgrupos. Realizar la gráfica de control para la siguiente serie de
datos obtenida durante el muestreo.
Muestra Latas defectuosas Muestra Latas defectuosas
np np
1 12 16 8
2 15 17 10
3 8 18 5
4 10 19 13
5 4 20 11
6 7 21 20
7 16 22 18
8 9 23 24
9 14 24 15
10 10 25 9
11 5 26 12
12 6 27 7
13 17 28 13
14 12 29 9
15 22 30 6

14. Pág. 14
Calcule la fracción defectuosa para cada muestra:
2313.p
n
pp
pLSCp
)1(
3

 =
50
77.*23.
32313.  =.4102
n
pp
pLICp
)1(
3

 =
50
77.*23.
32313.  =.05243
Trazando la gráfica
Muestra Latas defectuosas Fracción defectuosa Muestra Latas defectuosas Fracción defectuosa
np p np p
1 12 0.24 16 8 0.16
2 15 0.30 17 10 0.20
3 8 0.16 18 5 0.10
4 10 0.20 19 13 0.26
5 4 0.08 20 11 0.22
6 7 0.14 21 20 0.40
7 16 0.32 22 18 0.36
8 9 0.18 23 24 0.48
9 14 0.28 24 15 0.30
10 10 0.20 25 9 0.18
11 5 0.10 26 12 0.24
12 6 0.12 27 7 0.14
13 17 0.34 28 13 0.26
14 12 0.24 29 9 0.18
15 22 0.44 30 6 0.12
3020100
0.5
0.4
0.3
0.2
0.1
0.0
Sample Number
Proportion
P Chart for C1
1
1
P=0.2313
UCL=0.4102
LCL=0.05243

15. Pág. 15
Gráfica np – Número de defectivos
La gráfica np es basada en el número de defectuosos en vez de la proporción de defectuosos. Los
límites son calculados mediante la siguientes fórmulas.
 pnpnpLSC  13
 pnpnpLIC  13
Ejemplo 5:
Utilizando los datos del diagrama anterior, construya la gráfica np e interprete los resultados.
De la tabla obtenemos 2313.0p , n = 50.
Calculando los límites de control tenemos:
LSC =     510.207687.02313.0503)2313.0)(50( 
LIC =     620.27687.02313.0503)2313.0)(50( 
Gráfico de Control C.
3020100
25
20
15
10
5
0
Sample Number
SampleCount
NP Chart for cantidad
1
1
NP=11.57
3.0SL=20.51
-3.0SL=2.621

16. Pág. 16
Gráfica C – para número de defectos
Se utiliza para determinar la ocurrencia de defectos en la inspección de una unidad de producto.
Esto es determinar cuantos defectos tiene un producto. Podemos tener un grupo de 5 unidades de
producto, 10 unidades, etc.
Los límites de control se calculan mediante las siguientes fórmulas:
ccLSC 3
ccLSC 3
Donde:
c = total de defectos/ número de unidades de producto.
Ejemplo:
En la siguiente tabla tenemos el número de unidades de defectos observados en 26 muestras
sucesivas de 100 filtros de seguridad.
muestra defectos muestra defectos
1 21 14 19
2 24 15 10
3 16 16 17
4 12 17 13
5 15 18 22
6 5 19 18
7 28 20 39
8 20 21 30
9 31 22 24
10 25 23 16
11 20 24 19
12 24 25 17
13 16 26 15
67.19
26
516
c
37.667.19367.19
97.3267.19367.19


LIC
LSC

17. Pág. 17
Grafica U – Defectos por Unidad
El diagrama u se basa en el promedio de defectos por unidad inspeccionada:
u =
n
c
donde
c = número de defectos
n = cantidad de piezas inspeccionadas
Para determinar los limites de control utilizamos las fórmulas siguientes:
n
u
uLSC 3
n
u
uLIC 3
Ejemplo 62
Una compañía que fabrica computadoras personales desea establecer un diagrama de control del
número de defectos por unidad. El tamaño de muestra es de cinco computadoras. En la tabla se
muestran el numero de defectos en 20 muestras de 5 computadoras cada una. Establecer el
diagrama de control u
2
Statistical Quality Control, Douglas C. Montgomery, Second Edition pp.181
20100
40
30
20
10
0
Sample Number
SampleCount
C Chart for C1
1
1
C=19.85
3.0SL=33.21
-3.0SL=6.481

18. Pág. 18
muestra tamaño de muestra Número de defectos, c promedio de defectos por unidad u
1 5 10 2
2 5 12 2.4
3 5 8 1.6
4 5 14 2.8
5 5 10 2
6 5 16 3.2
7 5 11 2.2
8 5 7 1.4
9 5 10 2
10 5 15 3
11 5 9 1.8
12 5 5 1
13 5 7 1.4
14 5 11 2.2
15 5 12 2.4
16 5 6 1.2
17 5 8 1.6
18 5 10 2
19 5 7 1.4
20 5 5 1
Total 193 38.6
93.1
20
60.38


n
u
u i
Los límites de control son los siguientes:
79.3
5
93.1
393.1 LSC
07.0
5
93.1
393.1 LIC
20100
4
3
2
1
0
Sample Number
SampleCount
U Chart for C1
U=1.930
3.0SL=3.794
-3.0SL=0.06613