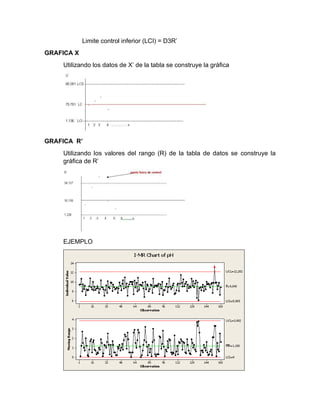
Este documento explica los gráficos de control por variables (gráficos X-R), incluyendo su definición, tipos, y cómo construirlos y analizarlos. Los gráficos X-R permiten evaluar si un proceso está bajo control estadístico mediante el monitoreo de datos a lo largo del tiempo y la identificación de puntos que caen fuera de los límites de control, lo que indica la presencia de causas especiales que deben ser investigadas. El documento proporciona instrucciones paso a paso para construir gráf

1. UNIVERSIDAD DE CARTAGENA
PROGRAMA: ADMINISTRACION DE EMPRESAS
PROTOCOLO
PROGRAMA Administración de empresas
ASIGNATURA Control estadístico de la calidad
TEMA Gráficos de control por variables

2. 1. Definición de gráficos de control
Se puede definir a la gráfica de control como un método gráfico para evaluar si un
proceso está o no en un "estado de control estadístico". En su forma más usual, la
gráfica de control es una comparación gráfica cronológica (hora a hora, día a día)
de las características de calidad reales del producto, parte o unidad, con límites
que reflejan la capacidad del producirla de acuerdo con la experiencia de las
características de calidad
Las variaciones podían ser de dos clases: una aleatoria, entendiendo por ella que
su causa era insignificante o desconocida, y otra imputable (también
llamada asignable), cuyas causas podían ser descubiertas y eliminadas tras un
correcto diagnóstico.
Los gráficos de control constituyen una herramienta estadística utilizada para
evaluar la estabilidad de un proceso. Permite distinguir entre las causas de
variación. Todo proceso tendrá variaciones, pudiendo estas agruparse en:
Causas aleatorias de variación. Son causas desconocidas y con poca
significación, debidas al azar y presentes en todo proceso.
Causas específicas (imputables o asignables). Normalmente no deben estar
presentes en el proceso. Provocan variaciones significativas.
Las causas aleatorias son de difícil identificación y eliminación. Las causas
específicas sí pueden ser descubiertas y eliminadas, para alcanzar el objetivo de
estabilizar el proceso.
2. Tipos de gráficas de control por variables
Gráficos o cartas X- R: Fundamento, donde y para que se usan.
Un gráfico de control es un diagrama especialmente preparado donde se van
anotando los valores sucesivos de la característica de calidad que se está
controlando. Los datos se registran durante el funcionamiento del proceso de
fabricación y a medida que se obtienen.
Todo grafico de control está diseñado para presentar los siguientes
principios:
Fácil de entendimiento de los datos, Claridad, Consistencia, Medir variaciones de
calidad, Como se elaboran, Como se leen e interpretan.

3. El gráfico de control tiene:
Línea Central que representa el promedio histórico de la característica que se
está controlando.
Límites Superior e Inferior que calculado con datos históricos presentan los
rangos máximos y mínimos de variabilidad.
Subgrupos
Grupo de mediciones con algún criterio similar obtenidas de un proceso
Se realizan agrupando los datos de manera que haya máxima variabilidad entre
subgrupo y mínima variabilidad dentro de cada subgrupo
Media
Sumatoria de todos los subgrupos divididos entre el número de muestras
Rango
Valor máximo menos el valor mínimo.
Utilidad.
Los gráficos x-R se utilizan cuando la característica de calidad que se desea
controlar es una variable continua.
Paso # 1 Recolección de datos.
Estos datos deberán ser:
Recientes de un proceso al cual se quiere controlar
Estos pueden ser tomados
Diferentes horas del día
Diferentes días
Todos tienen que ser de un mismo producto.
Paso # 2 Promedio
Sumatoria de los datos de cada uno de los subgrupos dividido entre el número de
datos (n).

4. Formula X
∑X1 + X2 + X3 + Xn
n
La fórmula debe ser utilizada para cada uno de los subgrupos.
Paso # 3 Rango
Valor mayor del subgrupo menor el valor menor.
Formula
R = x valor mayor – x valor menor
Determine el rango para cada uno de los subgrupos
Paso # 4 promedio global.
Sumatoria de todos los valores medios y se divide entre el número de
subgrupos (k).
Formula X’
∑X1 + X2 + X3 +…+ Xn
K
Paso # 5 Valor Medio Del Rango
Sumatoria del rango (R) de cada uno de los subgrupos divido entre el
numero de subgrupos (k).
Formula R’
∑R1 + R2 + R3 + …. + Rn
K

5. EJEMPLO DE TABLA DE DATOS
Paso # 6 Limite de Control
Para calcular los límites de control se utilizan los datos de la siguiente tabla
Gráfica X’
Línea central (LC) = X’
Limite control superior (LCS ) = X’ + A2R’
Limite control inferior (LCI ) = X’ - A2R’
Gráfica de R’
Línea central (LC ) = R’
Limite control superior (LCS) = D4R’

6. Limite control inferior (LCI) = D3R’
GRAFICA X
Utilizando los datos de X’ de la tabla se construye la gráfica
GRAFICA R’
Utilizando los valores del rango (R) de la tabla de datos se construye la
gráfica de R’
EJEMPLO

7. Puntos fuera de Control
Identificación de causas especiales o asignables Pautas de comportamiento que
representan cambios en el proceso:
Un punto exterior a los límites de control.
Se estudiará la causa de una desviación del comportamiento tan fuerte
Dos puntos consecutivos muy próximos al límite de control.
La situación es anómala, estudiar las causas de variación.
Cinco puntos consecutivos por encima o por debajo de la línea central.
Investigar las causas de variación pues la media de los cinco puntos indica una
desviación del nivel de funcionamiento del proceso.
Fuerte tendencia ascendente o descendente marcada por cinco puntos
consecutivos.
Investigar las causas de estos cambios progresivos.
Cambios bruscos de puntos próximos a un límite de control hacia el otro
límite.
Examinar esta conducta errática
Proceso bajo control
Si no hay puntos fuera de los límites de control y no se encuentran patrones no
aleatorios, se adoptan los límites calculados para controlar la producción futura
Una vez determinado que el proceso está bajo control estadístico entonces se
puede evaluar la capacidad del proceso
3. Con los datos que se tomaron de los pesos de los diabolines, (SOLO A
LOS PESOS) construya los Gráficos X – R y hágale los respectivos análisis
(ARCHIVO EXCEL)