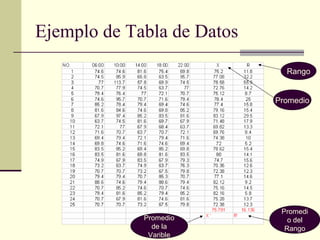
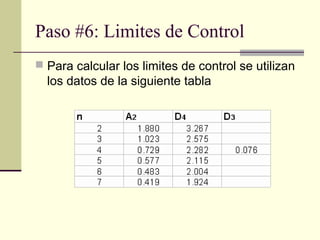
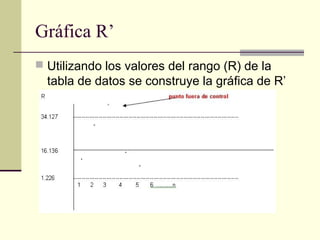
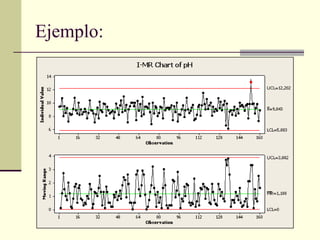
Un gráfico de control es una herramienta estadística para monitorear procesos de fabricación. Muestra la línea central promedio, límites superior e inferior calculados con datos históricos, y valores sucesivos medidos. Si los puntos están dentro de los límites, el proceso está bajo control estadístico. Si hay puntos fuera de los límites o patrones no aleatorios, se debe investigar las causas para mejorar el proceso.

1. Gráfica de Control
Para Data Continua
Profesor Walter López

2. Introducción
 Un gráfico de control es un diagrama
especialmente preparado donde se van
anotando los valores sucesivos de la
característica de calidad que se está
controlando.
 Los datos se registran durante el
funcionamiento del proceso de fabricación y
a medida que se obtienen.

3. Objetivo General
 Objetivo General
 Todo grafico de control esta diseñado para
presentar los siguientes principios:
 Fácil de entendimiento de los datos
 Claridad
 Consistencia
 Medir variaciones de calidad

4. Objetivo Específico
 Proceso de prevención para evitar que el
producto llegue sin defectos al cliente.
 Detectar y corregir variaciones de calidad

5. Definición de los términos
 El gráfico de control tiene:
 Línea Central que representa el promedio
histórico de la característica que se está
controlando
 Límites Superior e Inferior que calculado
con datos históricos presentan los rangos
máximos y mínimos de variabilidad.

6. Definición de Términos
 Subgrupos
 Grupo de mediciones con algún criterio similar
obtenidas de un proceso
 Se realizan agrupando los datos de manera que haya
máxima variabilidad entre subgrupo y mínima
variabilidad dentro de cada subgrupo
 Media
 Sumatoria de todos los subgrupos divididos entre el
numero de muestras
 Rango
 Valor máximo menos el valor mínimo

7. Utilidad
 Los gráficos x-R se utilizan cuando la
característica de calidad que se desea
controlar es una variable continua.

8. Paso #1:Recolección de Datos
 Estos datos deberán ser:
 Recientes de un proceso al cual se quiere
controlar
 Estos pueden ser tomados
 Diferentes horas del día
 Diferentes días
 Todos tienen que ser de un mismo producto.

9. Paso #2: Promedio
 Sumatoria de los datos de cada uno de los
subgrupos dividido entre el numero de datos
(n).
 Formula X
 ∑X1 + X2 + X3 + Xn
n
 La formula debe ser utilizada para cada uno de
los subgrupos

10. Paso #3: Rango
 Valor mayor del subgrupo menor el valor
menor.
 Formula
 R = x valor mayor – x valor menor
 Determine el rango para cada uno de los
subgrupos

11. Paso #4: Promedio Global
 Sumatoria de todos los valores medios y se
divide entre el número de subgrupos (k).
 Formula X’
 ∑X1 + X2 + X3 +…+ Xn
k

12. Paso #5: Valor Medio del Rango
 Sumatoria del rango (R) de cada uno de los
subgrupos divido entre el numero de
subgrupos (k).
 Formula R’
 ∑R1 + R2 + R3 + …. + Rn
k

13. Ejemplo de Tabla de Datos
Rango
Promedio
Promedi
Promedio o del
de la Rango
Varible

14. Paso #6: Limites de Control
 Para calcular los limites de control se utilizan
los datos de la siguiente tabla

15. Limites de control
 Gráfica X’
 Línea central (LC) = X’
 Limite control superior (LCS ) = X’ + A2R’
 Limite control inferior (LCI ) = X’ - A2R’
 Gráfica de R’
 Línea central (LC ) = R’
 Limite control superior (LCS) = D4R’
 Limite control inferior (LCI) = D3R’

16. Gráfica X’
 Utilizando los datos de X’ de la tabla se
contruye la gráfica

17. Gráfica R’
 Utilizando los valores del rango (R) de la
tabla de datos se construye la gráfica de R’

18. Ejemplo:

19. Puntos fuera de Control
Identificación de causas especiales o asignables
Pautas de comportamiento que representan cambios en el proceso:
 Un punto exterior a los límites de control.
 Se estudiará la causa de una desviación del comportamiento tan
fuerte.
 Dos puntos consecutivos muy próximos al límite de control.
 La situación es anómala, estudiar las causas de variación.
 Cinco puntos consecutivos por encima o por debajo de la línea central.
 Investigar las causas de variación pues la media de los cinco
puntos indica una desviación del nivel de funcionamiento del
proceso.
 Fuerte tendencia ascendente o descendente marcada por cinco
puntos
consecutivos.
 Investigar las causas de estos cambios progresivos.
 Cambios bruscos de puntos próximos a un límite de control hacia el
otro
límite.
 Examinar esta conducta errática.

20. Proceso bajo control
 Si no hay puntos fuera de los límites de
control y no se encuentran patrones no
aleatorios, se adoptan los límites calculados
para controlar la producción futura
 Una vez determinado que el proceso esta
bajo control estadístico entonces se puede
evaluar la capacidad del proceso.

21. Conclusión
 Los gráficos de control son herramientas
estadísticas
 Muy simples de construir
 Simples de utilizar
 Muy útiles para controlar tendencias y la
estabilidad de un proceso analítico.

22. Referencias
 E.L. Grant, R.S. Leavenworth, Statistical Quality Control, McGraw-Hill,
Inc., New York (1988)
 D.L. Massart, B.G.M. Vandeginste, L.M.C. Buydens, S. De Jong, P.J.
Lewi, J.Smeyers-Verbeke, Handbook of Qualimetrics and
Chemometrics. Part A. Elsevier, Ámsterdam (1997)
 http://www.quimica.urv.es/quimio
 Escalona Moreno, Iván. Unidad Profesional Interdisciplinaria de
Ingeniería y Ciencias sociales y Administrativas (UPIICSA) del Instituto
Politécnico Nacional (I.P.N.), México (2002).
 Armando Moreno, Diego. Campus Piedras Negras Calidad Piedras
Negras Coahuila, México (2005).
Colaboración:
Ivonne M. Ferrer Lassala