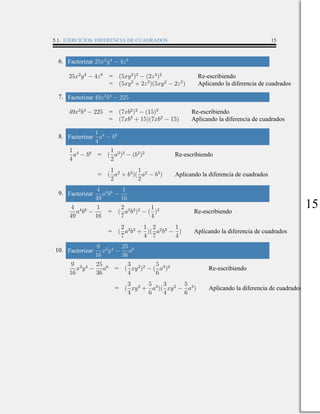
Este documento presenta diferentes técnicas para factorizar expresiones algebraicas, incluyendo encontrar un factor común, factorizar un binomio como factor común, factorización completa, diferencia de cuadrados, trinomio cuadrado perfecto y factorización de trinomios. Incluye ejemplos y ejercicios resueltos de cada técnica.