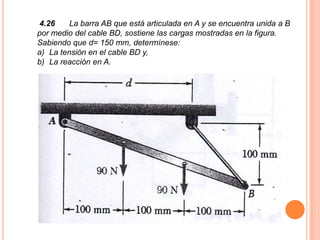
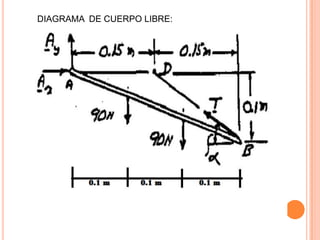
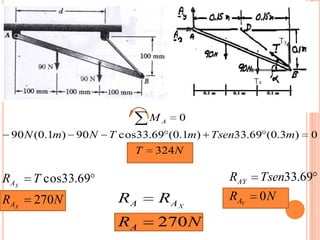
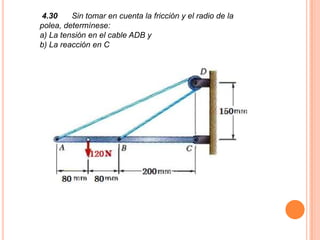
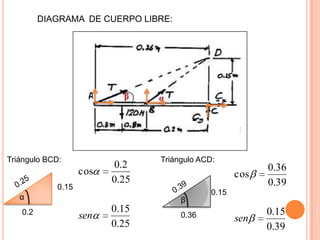
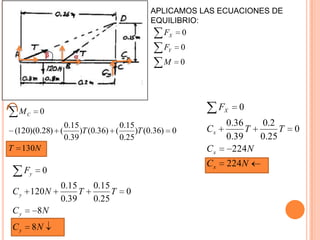
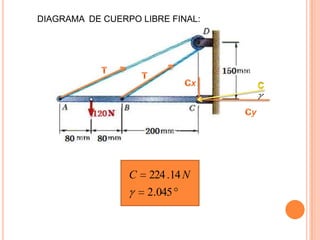
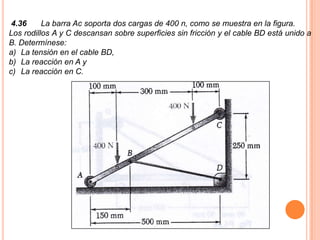
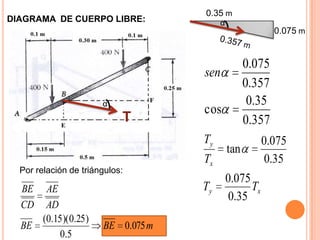
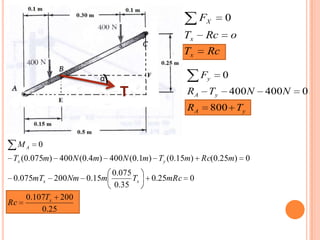
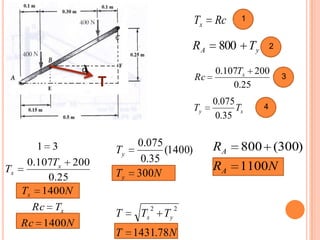
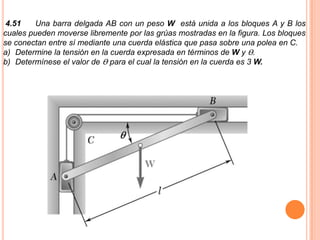
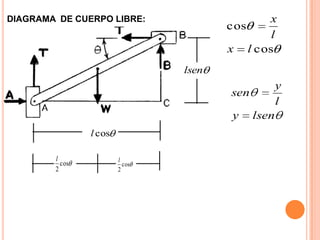
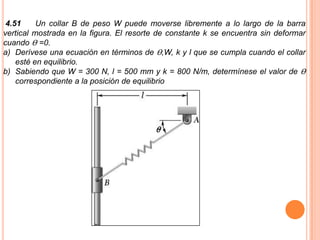
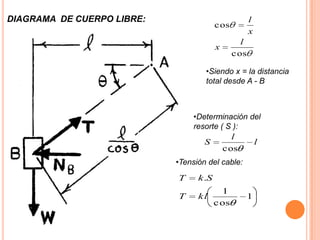
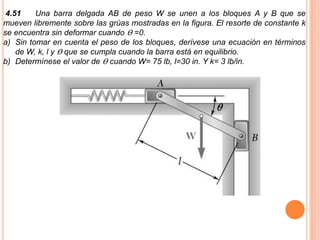
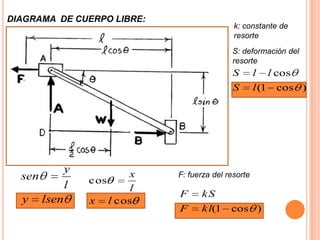
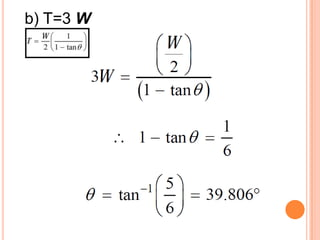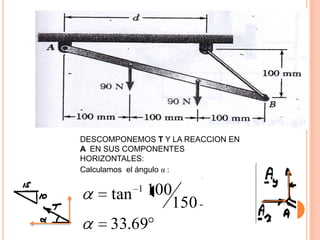
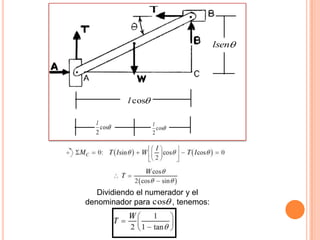
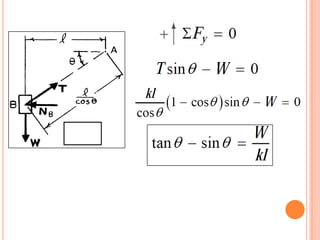
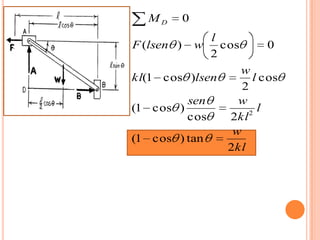
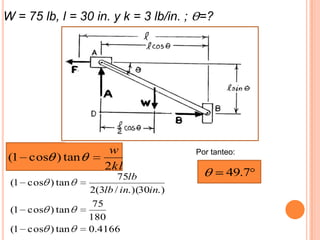
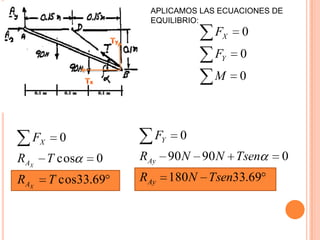
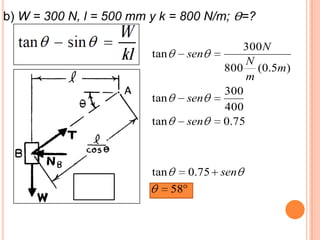
1) Se presenta un diagrama de cuerpo libre con una barra AB unida a bloques A y B a través de grúas. Un resorte conecta la barra cuando Θ = 0. 2) Se deriva una ecuación en términos de W, k, l y Θ para cuando la barra está en equilibrio. 3) Para W= 75 lb, l=30 in, k= 3 lb/in, se determina que Θ = 49.7° cuando la barra está en equilibrio.

2. 4.26 La barra AB que está articulada en A y se encuentra unida a B
por medio del cable BD, sostiene las cargas mostradas en la figura.
Sabiendo que d= 150 mm, determínese:
a) La tensión en el cable BD y,
b) La reacción en A.

3. DIAGRAMA DE CUERPO LIBRE:

4. DESCOMPONEMOS T Y LA REACCION EN
A EN SUS COMPONENTES
HORIZONTALES:
Calculamos el ángulo α :
tan 100
1
150
33.69

5. APLICAMOS LAS ECUACIONES DE
EQUILIBRIO:
FX 0
FY 0
M 0
FX 0 FY 0
RAX T cos 0 RAy 90 N 90 N Tsen 0
RAX T cos33.69 RAy 180N Tsen33.69

6. Ty
Tx
MA 0
90 N (0.1m) 90 N T cos33.69 (0.1m) Tsen33.69 (0.3m) 0
T 324N
RAX T cos33.69 RAY Tsen33.69
RAX 270N RA RA X RAY 0N
RA 270N

7. 4.30 Sin tomar en cuenta la fricción y el radio de la
polea, determínese:
a) La tensión en el cable ADB y
b) La reacción en C

8. DIAGRAMA DE CUERPO LIBRE:
Triángulo BCD: Triángulo ACD:
0.2 0.36
cos cos
0.25 0.39
0.15
0.15
α β
0.2 0.15 0.15
sen 0.36 sen
0.25 0.39

9. APLICAMOS LAS ECUACIONES DE
EQUILIBRIO:
FX 0
FY 0
M 0
MC 0 FX 0
0.15 0.15 0.36 0.2
(120)(0.28) ( )T (0.36) ( )T (0.36) 0 Cx T T 0
0.39 0.25 0.39 0.25
T 130N Cx 224N
Cx 224N
Fy 0
0.15 0.15
C y 120 N T T 0
0.39 0.25
Cy 8N
Cy 8N

10. DIAGRAMA DE CUERPO LIBRE FINAL:
C 224 .14 N
2.045

11. 4.36 La barra Ac soporta dos cargas de 400 n, como se muestra en la figura.
Los rodillos A y C descansan sobre superficies sin fricción y el cable BD está unido a
B. Determínese:
a) La tensión en el cable BD,
b) La reacción en A y
c) La reacción en C.

12. 0.35 m
DIAGRAMA DE CUERPO LIBRE: α
0.075 m
0.075
sen
0.357
α 0.35
cos
T 0.357
Ty 0.075
tan
Tx 0.35
Por relación de triángulos:
0.075
BE AE Ty Tx
0.35
CD AD
(0.15 )( 0.25 )
BE BE 0.075 m
0.5

13. FX 0
Tx Rc o
Tx Rc
α Fy 0
T RA Ty 400N 400N 0
RA 800 Ty
MA 0
Tx (0.075m) 400 N (0.4m) 400N (0.1m) Ty (0.15m) Rc(0.25m) 0
0.075
0.075mTx 200Nm 0.15m Tx 0.25mRc 0
0.35
0.107Tx 200
Rc
0.25

14. Tx Rc 1
RA 800 Ty 2
α 0.107Tx 200
Rc 3
T 0.25
0.075 4
Ty Tx
0.35
1 3 0.075 RA 800 (300)
Ty (1400)
0.107Tx 200 0.35
Tx RA 1100N
0.25 Ty 300N
Tx 1400N
Rc Tx 2 2
T Tx Ty
Rc 1400N
T 1431.78N

15. 4.51 Una barra delgada AB con un peso W está unida a los bloques A y B los
cuales pueden moverse libremente por las grúas mostradas en la figura. Los bloques
se conectan entre sí mediante una cuerda elástica que pasa sobre una polea en C.
a) Determine la tensión en la cuerda expresada en términos de W y ϴ.
b) Determínese el valor de ϴ para el cual la tensión en la cuerda es 3 W.

16. DIAGRAMA DE CUERPO LIBRE: x
cos
l
x l cos
lsen
y
sen
l
y lsen
l cos
l l
cos cos
2 2

17. lsen
l cos
l l
cos cos
2 2
Dividiendo el numerador y el
denominador para cos , tenemos:

18. b) T=3 W

19. 4.51 Un collar B de peso W puede moverse libremente a lo largo de la barra
vertical mostrada en la figura. El resorte de constante k se encuentra sin deformar
cuando ϴ =0.
a) Derívese una ecuación en términos de ϴ,W, k y l que se cumpla cuando el collar
esté en equilibrio.
b) Sabiendo que W = 300 N, l = 500 mm y k = 800 N/m, determínese el valor de ϴ
correspondiente a la posición de equilibrio

20. DIAGRAMA DE CUERPO LIBRE: l
cos
x
l
x
cos
•Siendo x = la distancia
total desde A - B
•Determinación del
resorte ( S ):
l
S l
cos
•Tensión del cable:
T k .S
1
T kl 1
cos

22. b) W = 300 N, l = 500 mm y k = 800 N/m; ϴ=?
300 N
tan sen
N
800 (0.5m)
m
300
tan sen
400
tan sen 0.75
tan 0.75 sen
58

23. 4.51 Una barra delgada AB de peso W se unen a los bloques A y B que se
mueven libremente sobre las grúas mostradas en la figura. El resorte de constante k
se encuentra sin deformar cuando ϴ =0.
a) Sin tomar en cuenta el peso de los bloques, derívese una ecuación en términos
de W, k, l y ϴ que se cumpla cuando la barra está en equilibrio.
b) Determínese el valor de ϴ cuando W= 75 lb, l=30 in. Y k= 3 lb/in.

24. DIAGRAMA DE CUERPO LIBRE:
k: constante de
resorte
S: deformación del
resorte
S l l cos
S l (1 cos )
y x F: fuerza del resorte
sen cos
l l
F kS
y lsen x l cos
F kl(1 cos )

25. MD 0
l
F (lsen ) w cos 0
2
w
kl(1 cos )lsen l cos
2
sen w
(1 cos ) 2
l
cos 2kl
w
(1 cos ) tan
2kl

26. W = 75 lb, l = 30 in. y k = 3 lb/in. ; ϴ=?
w Por tanteo:
(1 cos ) tan
2kl
75lb 49.7
(1 cos ) tan
2(3lb / in.)(30in.)
75
(1 cos ) tan
180
(1 cos ) tan 0.4166