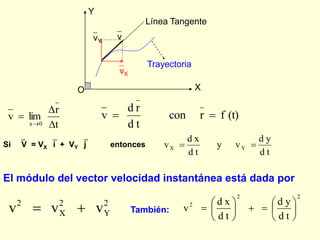
El documento aborda el concepto de movimiento curvilíneo, describiendo aspectos como los vectores de posición, desplazamiento, velocidad media e instantánea, y aceleración. Se incluyen ejemplos de cómo calcular estos vectores y sus derivadas a partir de ecuaciones que definen la trayectoria de partículas en movimiento. También se exploran movimientos compuestos y el movimiento parabólico, resaltando la independencia de los movimientos y sus componentes.

1. MOVIMIENTO CURVILÍNEO
Es aquel movimiento cuya trayectoria es una curva (
parábola, elipse, circunferencia, etc ).
Sea una partícula en movimiento, cuya trayectoria curvilínea
esta dada según la figura siguiente:
r1
r2
r
Trayectoria
O
Y
X

2. r1
r2
r
Trayectoria
O
Y
X
VECTOR POSICIÓN (r )
Es aquel vector que ubica a un punto de
la trayectoria de una partícula en
movimiento y puede variar con respecto
al tiempo
r = x i + y j con x = f (t) y = f (t)
r = x(t) i + y(t) j
VECTOR DESPLAZAMIENTO: r
Es aquel vector que ubica un punto de la trayectoria con respecto a
otro punto de la misma trayectoria.
r = r2 - r1

3. EJEMPLO
Las coordenadas de una partícula en movimiento están dadas por
las siguientes ecuaciones: x = 2 t2 y =3 t – 1 donde x e y están
en metros y t en segundo. Calcular el vector desplazamiento para la
partícula para t = 1 s y t = 3 s
SOLUCIÓN
j
y(t)
i
x(t)
r1 

j
1)
-
t
3
(
i
)
(2t
r 2
1 

j
1)
-
1
3
(
i
(1)
2
r 2
1 x


j
2
i
2
r1 

j
1)
-
3
3
(
i
(3)
2
r 2
3 x


j
8
i
18
r3 

1
3 r
r
r 


j
)
2
8
(
i
)
2
18
(
r 




j
6
i
16
r 



4. VELOCIDAD MEDIA ( vm, )
Es aquel vector que se define como el cociente entre el
desplazamiento (r ) y el intervalo de tiempo ( t ), es decir:
t
r
vm



EJEMPLO
Una partícula en movimiento curvilíneo está definida por:
x = t2 – t + 1 y = 3 t
Donde “x” e “y” están en metro y “t” en segundo. Calcular el vector
velocidad media, el módulo y dirección entre t = 1 s y t = 3 s
SOLUCIÓN
1
3
r
r
t
r
v
1
3
m






j
)
3
3
(
i
)
1
3
3
(
r 2
3 x




j
9
i
7
r3 

j
)
1
3
(
i
)
1
1
1
(
r 2
1 x




j
3
i
r1 

2
i
6
i
6
1
3
r
r
v
1
3
m





i
3
i
3
vm 


5. VELOCIDAD INSTANTÁNEA ( v )
El vector velocidad instantánea de una partícula en
movimiento curvilíneo es la primera derivada del vector
posición (r ) de la partícula con respecto a el tiempo
La velocidad instantánea es tangente a un punto de la
trayectoria.
O
Y
X
Trayectoria
Línea Tangente
v
vY
vX

6. O
Y
X
Trayectoria
Línea Tangente
v
vY
vX
t
r
lim
v
0
x 



(t)
f
r
con
t
d
r
d
v 

Si V = VX i + VY j entonces
t
d
y
d
y v
t
d
x
d
v Y
X 

El módulo del vector velocidad instantánea está dada por
2
Y
2
X
2
v
v
v 
 También:
t
d
y
d
t
d
x
d
v
2
2
2
















7. EJEMPLO
En un movimiento curvilíneo el vector posición de una partícula en
función del tiempo está dada por:
r = ( 2 t2 – 2 )i + ( t2 + t )j , donde r está en metro y t en
segundo. Calcular el vector velocidad instantánea, su módulo y su
dirección en t = 1 s
SOLUCIÓN
j
dt
dy
i
dt
dx
dt
r
d
v 


j
1)
t
2
(
i
t)
4
(
v 


j
3
i
4
v 

s
1
t
Para 
Módulo
2
2
3
4
v 
 m/s
5
v 
Dirección
5
4
v
v
cos x


 º
53


º
37



8. ACELERACIÓN MEDIA (a )
Sea una partícula en movimiento, cuya trayectoria curvilínea esta dada
según la figura siguiente:
Sean las velocidades instantáneasv1 yv2 para los puntos P1 y P2.
Trayectoria
O
Y
X v, siempre se dirige hacia la
parte cóncava de la trayectoria
P1

1
v
P2

2
v
2
v
1
v
v

Se define la aceleración media de una partícula en el intervalo de tiempo
( t ) por:
t
v
am




9. 1
2
1
2
m
t
t
v
-
v
a


Donde v1 y v2 son las velocidades instantáneas en los puntos P1 y P2
respectivamente
EJEMPLO
Una partícula tiene un movimiento curvilíneo cuyas ecuaciones del
movimiento está dada por:
x = 4 t2 – 2 t y = 2 t2 – 5 donde “x” e “y” están en metro y
“t” en segundo. Calcular el vector velocidad media entre los tiempos
de 3 s y 1 s, además obtener el valor de dicha velocidad media
SOLUCIÓN
j
(4x3)
i
)
2
3
8
(
j
(4t)
i
2)
-
t
8
(
v3 



 x j
12
i
22
v3 

j
(4x1)
i
)
2
1
8
(
j
(4t)
i
2)
-
t
8
(
v1 



 x j
4
i
6
v1 

1
3
1
3
m
t
t
v
-
v
a


2
j
8
i
16
am


2
m m/s
)
j
4
i
(8
a 


10. ACELERACIÓN INSTANTÁNEA
El vector aceleración instantánea de una partícula es igual a la primera
derivada del vector velocidad instantánea con respecto al tiempo, es
decir:
t
v
Lim
a
0
x 



)
t
(
f
v
con
t
d
v
d
a 

)
t
d
x
d
(
t
d
d
a 
)
t
(
f
x
con
t
d
x
d
a 2
2


Es decir: la aceleración instantánea es igual a la segunda derivada del
vector posición con respecto al tiempo
La aceleración es un vector que tiene la dirección igual al cambio
instantáneo de la velocidad

11. La aceleración siempre está apuntando hacia la parte
cóncava de la trayectoria
En la figura adjunta se observa la velocidad y la aceleración
instantánea para los puntos P1 , P2 y P3
O
Y
X
Trayectoria
v1
v2
v3
a1
a2
a3
P1
P2
P3




12. EJEMPLO
El movimiento de una partícula está definida por las siguientes
ecuaciones:
x = 2 t4 – 2 t y = 5 t3 - 4 donde “x” e “y” están expresadas en
metro y “t” en segundo. Calcular el valor de la aceleración instantánea
para cualquier tiempo y para cuando
t = 1 s
SOLUCIÓN
2
t
8
v 3
X 

2
X t
24
a 
2
Y t
15
v 
t
30
aY 
j
t
30
i
t
24
a 2


j
)
1
(
30
i
(1)
24
a 2
1 

j
30
i
24
a1 


13. ACELERACIÓN TANGENCIAL Y NORMAL.
En la figura se tiene la trayectoria curvilínea de una partícula, donde se
observa que en un punto tal como (A) la aceleración (a ) apunta hacia
la parte cóncava de la trayectoria
En ciertos fenómenos físicos como el movimiento circular es necesario
descomponer la aceleración en forma tangencial a la trayectoria ( aT ) y
en forma perpendicular a dicha tangente (aN ).
vectorialmente se tiene
N
T a
a
a 

a = aTuT + aNuN
Línea Tangente
Línea Normal
uN
uT
aT
aN
Y
X
Trayectoria
A
O
a

14. Matemáticamente se
demuestra que:
t
d
v
d
a T
T


2
T
N
v
a 
 = AQ es el radio de curvatura
Línea Tangente
Línea Normal
uN
uT
aT
aN
Y
X
Trayectoria
A
O
a
Q
El punto Q es el centro de curvatura
La aceleración tangencial mide la variación del módulo de la
velocidad.
La aceleración normal mide la variación de la dirección de la
velocidad
El módulo de la aceleración en el punto A se determinar por:
a2 = (aT )2 + (aN )2 ó a2 = (aX )2 + (aY )2

15. OBSERVACIONES
En el movimiento circular se cumple:
t
d
v
d
a T
T 
R
v
a
2
N 
En el movimiento circular uniforme se cumple que
0
t
d
v
d
a T
T 

R
v
a
2
N 
En el movimiento circular uniformemente variado, se cumple
que
constante
t
d
v
d
a T
T 
 R
v
a
2
N 

16. EJEMPLO
El movimiento de una partícula se define por:
r = ( t2 + 1 )i + ( t3 – 1)j
donde “r” está en metro y “t” en segundo. Calcular el radio de
curvatura de la trayectoria cuando t = 1 s
j
t
3
i
t
2
v 2

 4
2
t
9
t
4
v 

2
2
4
2
3
T
t
9
4
t
18
4
t
9
t
4
2
36t
t
8
dt
dv
a







j
t
6
i
2
a 
 2
t
36
4
a 

2
N
2
T
2
a
a
a 
 2
N
2
2
a
)
13
22
(
)
40
( 

13
22
a
,
1
t
Para T 

40
a
,
1
t
Para 

3
aN 
13
v 1
T 

2
T
N
v
a
:
que
Sabemos 

17. 
2
T
N
v
a
:
que
Sabemos 
3
aN  13
v 1
T 
:
Pero


13
1,73
,
)
13
(
3
2


5
,
7
3
,
1
13




18. EJEMPLO
Las coordenadas de un cuerpo en movimiento son:
x = t2 y =( t–1)2. Hallar:
a) La ecuación cartesiana de la trayectoria
b) ¿Cuándo se tiene la velocidad mínima?
c) La aceleración tangencial y normal cuando t = 1 s
SOLUCIÓN
a) y =(t -1)2 = t2- 2t +1
y = x – 2x1/2 +1
b) y = t2- 2t +1
vY = 2t- 2
x = t2
vx = 2t
2
Y
2
X v
v
v 

2
2
t)
2
(
2)
-
(2t
v 

4
8t
-
8t
v 2


:
cuando
mínima
es
velocidad
La
0
dt
dv

0
4
t
8
8t
2
8
-
t
16
dt
dv
2




0
4
-
8t  s
0,5
t 

19. 4
t
8
8t
4
t
8
4
t
8
8t
2
8
t
16
dt
dv
a
c)
2
2
T









vY = 2t- 2
aY = 2
vx = 2t
ax = 2
j
2
i
2
a 
 2
2
a 
2
N
2
T
2
a
a
a 

4
)
1
(
8
8(1)
4
(1)
8
a
2
T




4
4
aT  2
aT 
2
N
2
2
a
)
2
(
)
2
(2 
 2
aN 

2
T
N
v
a
:
que
Sabemos 
2
2
2


m
2



20. MOVIMIENTO COMPUESTO
Es aquel movimiento que resulta de la combinación de dos o más
movimientos simples (MRU, MRUV). Si el movimiento compuesto se
debe a dos MRU, la trayectoria es una línea recta en la dirección de la
velocidad resultante
Si el movimiento compuesto se debe a un MRU y a un MRUV ó dos
MRUV, la trayectoria será una parábola.
PRINCIPIO DE LA INDEPENDENCIA DE LOS MOVIMIENTOS
Si una partícula tiene un movimiento compuesto, cada uno de los
movimientos componentes se cumple como si los demás no existiesen
d
t
vR
t
t
vP

21. MOVIMIENTO PARABÓLICO
Es un caso particular del movimiento compuesto, su trayectoria es
una parábola. Proviene de dos movimientos simples que son el MRU
y el MRUV.
Si un cuerpo se lanza formando un determinado ángulo con la horizontal,
éste describe una parábola como trayectoria; la componente vertical de la
velocidad disminuye conforme el cuerpo sube y aumenta conforme el
cuerpo cae, en cambio la componente horizontal permanece constante.
vocos
vocos
vosen
vosen
vocos

Y
X
vocos
vo


22. VO: Velocidad inicial del cuerpo
 : ángulo de tiro
x : alcance para un tiempo “t”
OA : alcance máximo
Vo cos : componente horizontal de la velocidad inicial, esta
componente es constante
Vo sen : componente vertical de la velocidad inicial, esta
componente es variable
OBSERVACIONES
El alcance es suficientemente pequeño para despreciar la curvatura de
la Tierra
La altura máxima es suficientemente pequeño para despreciar la
variación de la gravedad de la Tierra.
Se desprecia la resistencia del aire

23. EJEMPLO
Un bote a motor parte desde la orilla de un río con una velocidad constante de
40 m/s, perpendicular a él. Las aguas del río tienen una velocidad de 30 m/s y
el ancho de éste es de 160 m.
a) ¿Qué tiempo demora el bote en llegar a la otra orilla?
b) ¿Qué espacio se desfasa?
c) ¿Qué espacio recorre?
SOLUCIÓN
160 m
Vb= 40 m/s
a) Cálculo del tiempo
e = vb t
160 = 40 t t = 4 s
b) Cálculo del espacio desfasado
Vr = 30 m/s
Vr / b
ed
ed = vr t
ed = 30 x 4 ed = 120 m
b) Cálculo del espacio que recorre
En el triángulo rectángulo, por Pitágoras
120
160
d = 200 m

24. EJEMPLO
Calcular la mínima velocidad (vo) que puede tener la persona para
lograr pasar el obstáculo mostrado en la figura
5 m
37º
vo
5 m
v0
37º
vH
vV
Movimiento horizontal e = vH tV 5 = v0 cos37º tV ….... (1)
Movimiento vertical
-vV
vf = vi – g t
-vV = vV – g tV 2vV = g tV 2v0sen37º = 10 tV
(2) en (1)
0,2 v0sen37º = tV ……. (2)
5 = v0cos37º (0,2) v0 sen37º
v0 = 1,9 m/s

25. EJEMPLO
Se dispara un proyectil con una velocidad inicial v = 25i + 25j
m/s. Determine el ángulo que hacen los vectores velocidad y
aceleración en t = 3 s.
SOLUCIÓN
25
vocos
25

Y
X
A
O
a = g
v
g
β
Para t = 3 s
M, horizontal
La velocidad es constante
vH = 25 i
M, vertical
vf = vi – g t vf = 25 – (10) (3) vf = -5 vV = - 5 j
vV
vH
g
β
tg β = vH / vV
Se desea hallar el ángulo entre el vector v = 25 i – 5 j y g = -10 j
tg β = 25 / 5 = 5 β =

26. Una partícula se mueve en un plano de tal manera que las ecuaciones
del movimiento son: x = 3 + t + 2 t3 y = -1 + t + t2 en donde “x” e
“y” están en metro y “t” en segundo. Calcular la posición, la velocidad
y aceleración de la partícula en los siguientes casos:
a) En cualquier tiempo “t”
b) En t = 3 s
Vx= 1 + 6 t2 VY= 1 + 2 t
Cálculo de la posición para cualquier tiempo “t”
x = 3 + t + 2 t3 y = -1 + t + t2
Cálculo de la posición para: t = 3 s
x3 = 3 + 3 + 2 x33 y3 = -1 + 3 + 32 x3 = 3 + 3 + 2 x33 y3 = -1 + 3 + 32
x3 = 60 m y3 = 11 m
j
11
i
r 
 60
3
j
)
t
t
1
(
i
)
2t
t
3
(
r 2
3







Cálculo de la velocidad para cualquier tiempo “t”
j
t)
i
6t
1
v 2
2
1
(
)
( 



Cálculo de la velocidad para: t = 3 s
V3X = 1 + 6 . 32 V3Y = 1 + 2 . 3
V3X = 55 m/s V3Y= 7 m/s
ó
ó
ó
ó j
7
i
55
v3 


27. Cálculo de la aceleración para cualquier tiempo “t”
ax= 12 t m/s2 aY= 2 m/s2 ó j
2
i
t
a 
12
Cálculo de la aceleración para: t = 3 s
a3X = 12x 3 m/s2 a3Y= 2 m/s2 a3X = 36 m/s2 a3Y= 2 m/s2
ó j
2
i
a 
 36
3

28. Una partícula se mueve en el plano XY de tal manera que cumple
con las siguientes ecuaciones: vX = 4 t3 + 4 t vY = 0,4 t . Si la
posición de la partícula es (1,2) cuando t = 0 s. Encontrar las
coordenadas de la posición en cualquier instante y la ecuación
cartesiana de la trayectoria
vX = 4 t3 + 4 t
t
3
t
dt
dx
4
4 

t)dt
4
3
t
4
(
dx 

  

x
1
t
0
3
t)dt
4
(4t
dx
2
t
4
4
4t
1)
-
x
(
2
4


1
t
2
t
x 2
4



vY = 0,4 t
0,4t
dt
dy

dt
t
4
,
0
dy 
 

y
2
t
0
dt
t
4
,
0
dy
2
t
4
,
0
2)
-
y
(
2

2
t
0,2
y 2


2
t
0,2
2
-
y

4
2
2
t
0,2
2)
-
(y

1
2
,
0
2)
-
y
(
2
2
,
0
2)
-
(y
x
2
2
2




29. Se dispara una partícula con una velocidad inicial de vo = ( i + j )
m/s actuando una aceleración a = ( -i + j ) m/s2. Si en t = 0 s el
móvil se encuentra en el punto (0,2) m. Determinar el vector posición
en el instante t = 2 s
X
Y
●
(0,2)
MÉTODO 1
EJE X aX= -1 y vX= 1 MRUV
2
t
a
t
v
x
2
0 

2
(2)
(-1)
(1)(2)
x
2
3 

m
0
x3 
EJE Y aY= 1 y vY= 1 MRUV
2
(2)
(1)
(1)(2)
y
2
3 

m
4
y3 
Comenzó el movimiento en y = 2
m
6
2
4
y3 


●
(0,6)
r
r = 0 i + 6 j

30. MÉTODO 2
2
t
a
t
v
r
2
0 

2
2
)
j
i
(-
)(2)
j
i
(
j
2)
-
(y
i
0)
-
x
(
2





)
j
2
i
(-2
)
j
2
i
2
(
j
2)
-
(y
i
x)
( 




j
4
i
0
j
2)
-
(y
i
x)
( 


6
y
0
x 
