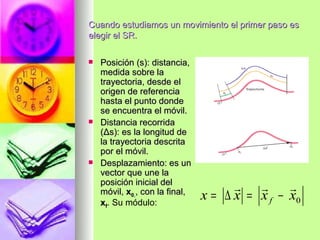
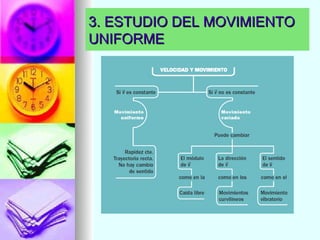
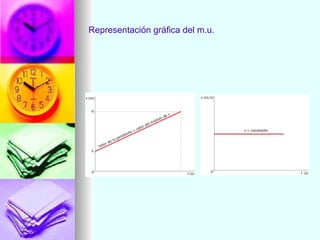
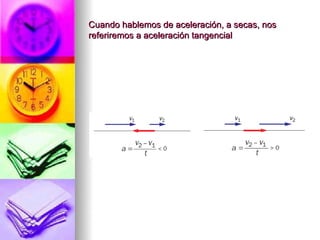
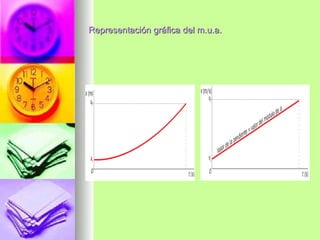
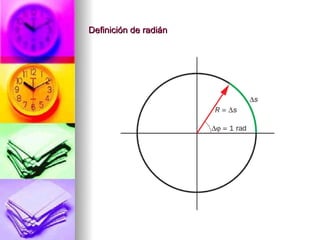
1. El documento describe los conceptos básicos de la cinemática, incluyendo el movimiento, trayectorias, magnitudes escalares y vectoriales. 2. Explica los tipos de movimiento como rectilíneo, curvilíneo y sus variaciones. También define la velocidad, rapidez, aceleración y movimientos uniforme y uniformemente acelerado. 3. Finalmente, analiza el movimiento circular uniforme, definiendo la velocidad angular, radián y aceleración centrípeta.

1. CINEMÁTICA
TEMA 1

2. 1. Características del movimiento
 En el universo todo está en continuo movimiento.
 Movimiento es el cambio de posición de un cuerpo
a lo largo del tiempo respecto a un sistema de
referencia (SR) que consideramos fijo.
 El movimiento es relativo; dependiendo del SR
utilizado las cosas se mueven o no y las
trayectorias adoptan una forma u otra.
 El SR elegido debe ser el que haga los cálculos
más sencillos.

3. Trayectoria: línea que une los puntos de las
sucesivas posiciones del móvil.
 Clasificación de los movimientos en función de la
trayectoria:
1. Rectilíneos
2. Curvilíneos: pueden ser
(a) Circulares
(b) Elípticos
(c) Parabólicos
(d) Irregulares

4. Magnitudes escalares y vectoriales
 Magnitudes escalares: son aquellas que se pueden
expresar mediante un número y sus unidades.
 Magnitudes vectoriales: son aquellas que para
definirlas es necesario conocer su módulo (valor
numérico), dirección y sentido. Se representan por
vectores (segmentos orientados).

5. Cuando estudiamos un movimiento el primer paso es
elegir el SR.
 Posición (s): distancia,
medida sobre la
trayectoria, desde el
origen de referencia
hasta el punto donde
se encuentra el móvil.
 Distancia recorrida
(Δs): es la longitud de
la trayectoria descrita
por el móvil.
 Desplazamiento: es un
vector que une la
posición inicial del
  
móvil, x0,, con la final,
xf. Su módulo:
x = ∆ x = x f − x0

6. La distancia recorrida, Δs, y el desplazamiento, Δx,
solo coinciden en el caso de que la trayectoria sea
rectilínea y no cambie el sentido de la marcha.
 La relatividad es una propiedad esencial del
movimiento: “Todo movimiento admite tantas
descripciones distintas como sistemas de
referencia se puedan elegir para observarlo”.
 Las leyes de la mecánica se cumplen de igual
modo en un sistema en reposo que en otro con
movimiento uniforme.

7. 2. La velocidad
 Para saber de qué modo varía la posición de un
móvil con el tiempo se definen rapidez y
velocidad.
 Rapidez es la relación entre la distancia recorrida y
el tiempo invertido. Es una magnitud escalar. En el
SI se mide en m/s.
∆s
Rapidez =
∆t

8. Rapidez instantánea es el valor al que tiende la rapidez
cuando el intervalo de tiempo en que se ha realizado la
medida se hace muy pequeño. Si el intervalo de tiempo es
grande hablamos de rapidez media.
 La velocidad es una magnitud vectorial. Es la
relación entre el desplazamiento y el tiempo
empleado. Su módulo se calcula con la siguiente
expresión:
∆x
v =
∆t
 Cuando el intervalo de tiempo es muy pequeño la
expresión anterior define la velocidad instantánea,
en caso contrario define la velocidad media.
 Cuando la trayectoria es curvilínea, la velocidad
instantánea es tangente a la trayectoria. Si es recta
lleva la misma dirección.

9. 3. ESTUDIO DEL MOVIMIENTO
UNIFORME

10. Movimiento uniforme, m.u.
 Cuando el vector velocidad se mantiene constante
no puede variar ni el módulo, ni la dirección, ni el
sentido del movimiento.
 La velocidad media coincide con la instantánea en
cualquiera de los puntos de la trayectoria que es
una recta.
 Se pueden utilizar indistintamente los términos
rapidez o velocidad, porque coinciden la distancia
recorrida y el desplazamiento.
x f − x0 ∆x
v= = → ∆ x = x f − x0 = v ⋅ t
t f − t0 ∆t

11. Despejando de la ecuación anterior y considerando t0
igual a cero obtenemos la ecuación de posición en
cualquier instante de un movimiento uniforme
x f = x0 + v ⋅ t

12. Representación gráfica del m.u.

13. 4. LA ACELERACIÓN
 Los movimientos más frecuentes no son los
uniformes sino los acelerados.
 Es necesario definir una nueva magnitud, la
aceleración (magnitud vectorial) que nos indicará
los cambios que se produzcan en el vector
velocidad, tanto en su módulo, en su dirección y
sentido. Para ello , definiremos la aceleración
tangencial y la aceleración normal.

14. Aceleración tangencial
 La aceleración tangencial, at, es la variación que
experimenta el módulo de la velocidad en el
tiempo.
v f − v0 ∆v
at = =
t f −t0 ∆t
 Al igual que la velocidad, la aceleración tangencial
es un vector tangente a la trayectoria en los
movimientos curvilíneos. Si la v y la at tienen el
mismo sentido el movimiento es acelerado, si
tienen sentidos opuestos será retardado.
 Se puede definir la aceleración media y la
instantánea al igual que en la velocidad. En el SI se
mide en m/s2.

15. Cuando hablemos de aceleración, a secas, nos
referiremos a aceleración tangencial

16. Aceleración normal
 Definimos la aceleración
normal, an, como el
cambio que experimenta
la dirección de la
velocidad con el tiempo.
 Es un vector
perpendicular a la
trayectoria, dirigido hacia
el centro de curvatura.
 El módulo de la
aceleración normal.
v2
an =
r

17. 5. EL MOVIMIENTO
UNIFORMEMENTE ACELERADO
 El movimiento uniformemente acelerado (m.u.a.) es
aquel en el que el módulo del vector velocidad (la
rapidez) varía de forma constante, pero no su
dirección ni su sentido. Se caracteriza por:
1. Seguir una trayectoria rectilínea. La distancia
recorrida y el desplazamiento coinciden.
2. Tener aceleración constante.
 Ecuación de la velocidad: la velocidad media en
este movimiento no es muy representativa, es más
interesante conocer su velocidad instantánea.
∆v
a= → v f = v0 + a ⋅ t
∆t

18. Ecuación de la posición
1
x f = x0 + v0 ⋅ t + ⋅ a ⋅ t 2
2
 La caída libre es un caso
particular del movimiento
uniformemente
acelerado.

19. Representación gráfica del m.u.a.

20. 6. El movimiento circular
uniforme
 El movimiento circular
uniforme (m.c.u.) es el de un
móvil que recorre una
trayectoria circular con
rapidez constante.
 La velocidad angular, ω, es
el ángulo barrido en la
unidad de tiempo.
∆ϕ
ω=
∆ t
 Donde Δφ es el ángulo
barrido expresado en
radianes, e Δt, el tiempo
transcurrido. Su unidad en el
SI es rad/s, o, simplemente,
s-1.

21. Definición de radián

22. El ángulo es la relación entre el arco y el radio con que
ha sido trazado
 Podemos deducir, por tanto, que:
Δs=φ·R
 Si dividimos los dos miembros de esta expresión
por el tiempo empleado obtendremos la siguiente
expresión:
v=ω·R
 Esta ecuación relaciona la velocidad angular y la
velocidad lineal.

23. Aceleración centrípeta: todos los movimientos
circulares son acelerados ya que cambia la dirección
del vector velocidad constantemente.
 Al no cambiar el módulo se trata de una aceleración
normal, an, perpendicular a la trayectoria, a la que
se denomina centrípeta, puesto que es un vector
dirigido hacia el centro de la circunferencia.
 Su módulo, en función de las velocidades lineal y
angular, es:
v 2
ω ⋅R 2 2
an = → an = = ω ⋅R
2
R R