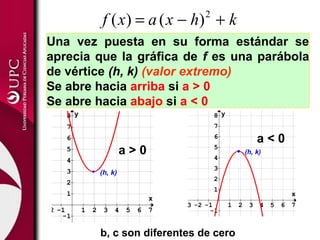
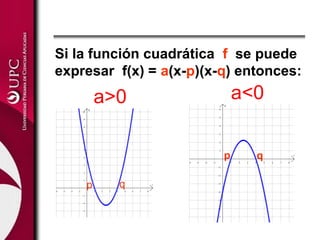
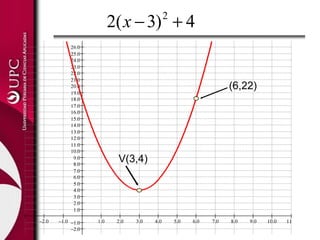
Este documento presenta conceptos sobre funciones lineales y cuadráticas. Explica la forma general de las funciones lineales y cuadráticas, e identifica sus elementos clave (pendiente, ordenada en el origen y vértice, respectivamente). Luego, aplica estas funciones a ejemplos como costos de producción, oferta y demanda. Finalmente, resuelve ejercicios prácticos usando funciones lineales y cuadráticas.

1. Matemática Básica para
Economistas MA99
Tema: Función Lineal y Función Cuadrática
UNIDAD 6
Clase 11.2

2. Objetivos:
• Presentar la fórmula general de la función lineal
e identificar sus elementos (pendiente y
ordenada en el origen)
• Presentar la fórmula general de la función
cuadrática e identificar sus elementos (vértice)
• Estudiar las aplicaciones de la función lineal y
cuadrática.

3. Función LinealFunción Lineal
f(x) = mx + bf(x) = mx + b
m es la pendiente de la ecuación de la recta
b es la ordenada en el origen
Cuando m = 0, la función se denomina
“función constante”
f(x) = bf(x) = b

4. Función LinealFunción Lineal
f(x) = mx + bf(x) = mx + b
-3 -2 -1 0 1 2 3
4
3
2
1
-1
-2
-3
b
Rfdom =)(

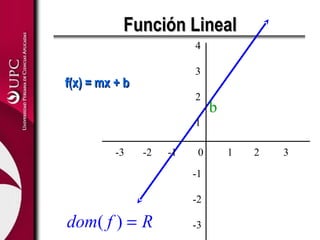
5. Ejemplo:Ejemplo: [ ]2,1;3)( −∈+= xxxf
−4 −3 −2 −1 1 2 3 4 5 6
1
2
3
4
5

6. f(x) = x
−5 −4 −3 −2 −1 1 2 3 4 5
−3
−2
−1
1
2
3
4
5Ejemplo:Ejemplo:
Función IdentidadFunción Identidad

7. f(x) = c
-2 -1 0 1 2
4
3
c
2
1
Ejemplo:Ejemplo:
Función ConstanteFunción Constante

8. Función Lineal: AplicacionesFunción Lineal: Aplicaciones
1. Los costos variables y fijos de producción de cierto artículo
son $30 y $24,000, respectivamente. Si el precio es de $40,
determine y grafique en un mismo sistema de coordenadas
las funciones de costo e ingreso. Determine el punto de
equilibrio y grafique la utilidad.
2. Dadas las funciones de oferta: p – q =10 y de demanda:
2p + q = 80. Si la gráfica de la función de oferta se traslada
en forma paralela de tal manera que el nuevo precio de
equilibrio es 28. Hallar la nueva ecuación de la oferta y la
cantidad de equilibrio correspondiente. Grafique.

9. Función Lineal: AplicacionesFunción Lineal: Aplicaciones
3. Un consumidor gasta siempre todo su ingreso (I) en la
compra de dos tipos de bienes (x,y) cuyos precios unitarios
son Px y Py.
a) Hallar y graficar una ecuación que represente todas las
combinaciones posibles de cantidades que se pueden
adquirir de cada bien.
b) ¿Cómo se traslada la gráfica si:
 Px se triplica?
 Px se reduce a la mitad?
 I se duplica?
 Ambos precios se duplican?

10. Aplicaciones:Aplicaciones:
Razón de cambio promedioRazón de cambio promedio
f
x
y
x∆
y∆P
Q
a b
f(a)
f(b)
QyPporpasaque
rectaladependienteRCP
ab
afbf
RCP
X
Y
RCP
=
−
−
=
∆
∆
=
)()(

11. La siguiente tabla muestra las ventas en dos años
diferentes en dos tiendas en una cadena de
tiendas de descuento.
Tienda Ventas en
1992
Ventas en
1995
A $100 000 $160 000
B $50 000 $140 000
Un estudio de los libros de la empresa sugiere que
las ventas de ambas tiendas han crecido
linealmente (es decir, las ventas pueden
aproximarse por una función lineal con bastante
precisión).
Aplicaciones:Aplicaciones:
Razón de cambio promedioRazón de cambio promedio

12. a) Encuentre una ecuación lineal que
describa las ventas de la tienda A
b) Encuentre una ecuación lineal que describa
las ventas de la tienda B
c) Encuentre la razón de cambio
promedio en “a”.
000100000x20y +=
00050000x30y +=
añopor00020$
3
00060$
en ventasR.C.P ==
Aplicaciones:Aplicaciones:
Razón de cambio promedioRazón de cambio promedio

13. d) Encuentre la razón de cambio promedio
en “b”.
Conclusión:
Si f(x) = mx +b es una función lineal,
entonces la razón de cambio promedio de
y con respecto a x es la pendiente de la recta
añopor00003$
3
00090$
en ventasR.C.P ==
e) Compare resultados
Aplicaciones:Aplicaciones:
Razón de cambio promedioRazón de cambio promedio

14. Suponga que el costo de producir radios –
reloj puede aproximarse mediante el
modelo lineal C(x) = 12x + 100
Costo Marginal
a) ¿Cuál es el costo de producir 0 radios-reloj?
b) ¿Cuál es el costo de producir 5 radios- reloj?
c) ¿Cuál es el costo de producir 6 radios- reloj?
d) ¿Cuál es el costo de producir el sexto radio?
e) ¿Cuál es el costo de producir el radio número 81?
f) ¿Cuál es el costo adicional por radio?
donde C(x) es el costo en dólares por
producir “x” radios- reloj.

15. Función CuadráticaFunción Cuadrática
f(x) = axf(x) = ax22
+ bx + c+ bx + c
Su gráfica es una parábola cuya forma
dependerá de los valores de a, b y c.
Por ejemplo:
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-2
-1
1
2
3
4
5
x
y

16. Función CuadráticaFunción Cuadrática
cbxaxy ++= 2
cx
a
b
xay +





+= 2
c
a
b
a
b
x
a
b
xay +














−





++=
22
2
22
a
b
c
a
b
xay
42
22
2
−+





+=
2
2
2
24






+=





−−
a
b
xa
a
b
cy
( )2
hxaky −=−
a
b
h
2
−=
a
b
ck
4
2
−=
ParábolaParábola

17. Una vez puesta en su forma estándar se
aprecia que la gráfica de f es una parábola
de vértice (h, k) (valor extremo)
Se abre hacia arriba si a > 0
Se abre hacia abajo si a < 0
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-2
-1
1
2
3
4
5
6
7
8
x
y
(h, k)
a > 0
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
(h, k)
a < 0
b, c son diferentes de cero
khxaxf +−= 2
)()(

18. 6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
(h, k)
a > 0
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
(h, k)
a < 0
Sea V(h,k) el vértice:
f(h) = k es el mínimo valor de f cuando a>0
f(h) = k es el máximo valor de f cuando a<0

19. Para cada función cuadrática
a. Exprese f en forma estándar
b. Trace la gráfica de f
c. Determine el valor extremo de f.
d. Intersecciones con los ejes.
e. Determine el valor de las funciones f y g
para x = -b/2a Analice.
49305)( 2
+−= xxxf
542)( 2
++−= xxxg
Ejemplos:Ejemplos:

20. Conclusión:Conclusión:
La gráfica de la función :
f(x) = a x2
+ b x + c
tiene su vértice en el punto de
coordenadas:
x= -b/2a ; y = f(-b/2a)
= c - b2
/4a

21. 1912x2xg(x) 2
−+−=
6xxh(x) 2
−−=
Para cada función cuadrática
a. Determine el valor extremo de f.
b. Intersecciones con los ejes.
c. Trace la gráfica de f.
Ejemplos:Ejemplos:

22. Cuando se traza la gráfica de una
función cuadrática, a la recta vertical
que pasa por el vértice se le denomina
“eje de simetría”
Si la gráfica de una función cuadrática
corta al eje “x” en dos puntos, la
abscisa del vértice es igual a la semi-
suma de las abscisas de estos puntos
de corte.
Un caso particularUn caso particular

23. Si la función cuadrática f se puede
expresar f(x) = a(x-p)(x-q) entonces:
a<0a>0
p q−18 −17 −16 −15 −14 −13 −12 −11 −10 −9 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8
−9
−8
−7
−6
−5
−4
−3
−2
−1
1
2
3
4
5
6
x
y
p q−11 −10 −9 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8
−6
−5
−4
−3
−2
−1
1
2
3
4
5
6
7
8
9
10
x
y

24. )5)(2(3 −−= xxf(x)
Trace la gráfica de las siguientes funciones:
)5)(1(3 −−−= xxg(x)
Ejemplo:Ejemplo:

25. Si tiene como datos al vértice y otro
punto de paso de una parábola, ¿cómo
puede obtener la regla de
correspondencia de la función que tiene
por gráfica a dicha parábola?
En otras palabras, teniendo h y k más
un punto (x,y) por donde pasa la gráfica,
¿podemos obtener la regla de
correspondencia?
Otro caso particularOtro caso particular

26. Ejemplo: Encuentre la regla de correspondencia de una función
cuadrática cuya gráfica tiene el vértice (3;4) y pasa por el punto
(6;,22).
1) Utilizamos khxa +− 2
)(
2) Para obtener 4)3( 2
+−xa
3) Por la información dada -pasa por el punto
(6,22)- sabemos que f(6) = 22
4)36(22 2
+−=a4) Por lo tanto:
5) De donde: 2
9
18 ==a
6) Finalmente: 4)3(2 2
+−x

27. −2.0 −1.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0 11.0
−2.0
−1.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
11.0
12.0
13.0
14.0
15.0
16.0
17.0
18.0
19.0
20.0
21.0
22.0
23.0
24.0
25.0
26.0
V(3,4)
(6,22)
4)3(2 2
+−x

28. Función CuadráticaFunción Cuadrática
AplicacionesAplicaciones
1. Al producir q artículos el costo total está dado por 1,500 +
12q dólares y el precio por p = 40 – q/20 dólares.
Determinar:
a) La función de utilidad y el punto de equilibrio. Graficar.
b) La utilidad máxima.
c) ¿Para qué cantidad de artículos se produce ganancia?
2. Dadas las ecuaciones de oferta: p = q2
/20 – q/5 + 16/5 y de
demanda: p = -q2
/30 – q/5 +76/5:
a) Graficarlas en un mismo plano.
b) Determine el punto de equilibrio.