El documento describe la integral definida y sus aplicaciones. La integral definida se define como el área bajo la curva de una función continua entre dos límites y puede usarse para calcular el área de figuras geométricas. También se usa para calcular el excedente del consumidor y productor, que representan el beneficio económico obtenido.

1. La Integral definida y susLa Integral definida y sus
AplicacionesAplicaciones

2. INTEGRAL DEFINIDA:INTEGRAL DEFINIDA:
DEFINICIÓNDEFINICIÓN
 La integral definida se define como:
 Donde F’(x) = f(x) y además f(x) es
una función continua y finita en el
intervalo de integración [a; b].
 a y b reciben el nombre de extremo
inferior y superior de integración,
respectivamente.
[ ] )()()()( aFbFxFdxxf
b
a
b
a
−==∫

3. ÁREA COMO LÍMITE DE UNAÁREA COMO LÍMITE DE UNA
SUMASUMA
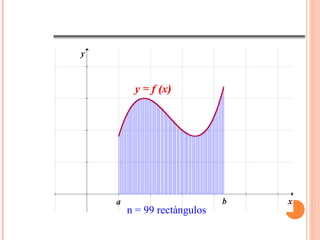
Considere la región definida por la
gráfica de la función y = f(x), el eje X y
las verticales x = a y x = b, siendo
f(x) ≥ 0 y f continua en el intervalo
[a; b].
Para abordar el problema de hallar el
área de dicha región, la relacionaremos
con áreas de figuras conocidas, por
ejemplo rectángulos

4. Ejemplo 1: La siguiente figura muestra laEjemplo 1: La siguiente figura muestra la
región cuya área se desea calcularregión cuya área se desea calcular
El área de una región podrá
plantearse por una integral
definida:
A = f(b) – f(a)

5. Dividiremos dicha región en rectángulos
verticales. Por ejemplo ...
n = 3 rectángulos

6. n = 6 rectángulos

7. n = 12 rectángulos

8. n = 24 rectángulos

9. n = 48 rectángulos

10. n = 99 rectángulos

11. La integral definida plantea el límite de una
suma de áreas.
Interpretación geométrica de la integral definidaInterpretación geométrica de la integral definida
∫=
b
a
dxxfÁrea )(
altura
ancho
Suma desde “a”
hasta “b”

12. EJEMPLO 2EJEMPLO 2
¿De cuántas formas podemos calcular el
área “R”?
[ ] 2222
0
2
2
0
402)2( uxdxx =−==∫
f(x) = 2x
0 2
R
Forma 1: Base*altura/2
2*4/2=4 u2
Forma 2: integral definida

13. Como acaba de verse, el área de una región
podrá plantearse como el límite de una suma
de áreas. Este límite está dado por la integral
definida:
∫=
a
b
dxxfA )(
Siempre que f(x) sea continua en [a; b] y
positiva en ese intervalo.

14. ¿CÓMO ESTÁ DEFINIDA EL ÁREA
SOMBREADA DE LOS
SIGUIENTES GRÁFICOS?
ANALICEMOS LOS SIGUIENTES
EJEMPLOS…….

15. EJEMPLO 3: ÁREA DEBAJO DELEJEMPLO 3: ÁREA DEBAJO DEL
EJE XEJE X
La altura no puede ser
negativa
∫−
b
a
dxxf )(Respuesta:

16. ÁREA POR ENCIMA Y DEBAJO DEL EJE X
∫
c
a
dxxf )(
+
La altura no puede ser
negativa
∫−
b
c
dxxf )(
Respuesta:

17. EJEMPLO 5: ÁREA ENTRE DOSEJEMPLO 5: ÁREA ENTRE DOS
CURVASCURVAS
¿Cómo podemos aplicar los conocimientos
previos a este gráfico?
Si se sabe que: )()( xgxf ≥ ∀ [ ]bax ,∈

18. EJEMPLO 5 (RECORDANDO..)
El área bajo
la curva f(x)
es…
El área bajo
la curva g(x)
es…

19. EJEMPLO 5
[ ]∫ −
b
a
dxxgxf )()(
Respuesta:

20. APLICACIONES DE LAAPLICACIONES DE LA
INTEGRAL DEFINIDAINTEGRAL DEFINIDA

21. 1. EXCEDENTE DEL CONSUMIDOR
2. El Excedente del Productor
3.Estimación del cambio neto, a partir de la razón de
cambio, en el valor de reventa de bienes capitales o en la
utilidad, ingresos y costos de una empresa
Aplicaciones de la Integral Definida
4.Estimación del exceso de utilidad de un plan de
inversión, respecto de otro

22. ANÁLISIS 1:
Recordando el concepto de la demanda
Una curva de demanda
resume la relación inversa existente entre precios y cantidades.
Una curva de demanda
refleja las cantidades que están dispuestos a comprar los
consumidores, ante determinados precios.
Una curva de demanda
representa la disponibilidad marginal de gastar de
parte del consumidor.
Demanda
Alimentos (unidades
mensuales)
Precio de
los alimentos
G
E
F
2,00$
4 12 20
1,00$
0,50$

23. ANÁLISIS 2:ANÁLISIS 2:
LA DISPONIBILIDAD TOTAL A GASTAR DE LOSLA DISPONIBILIDAD TOTAL A GASTAR DE LOS
CONSUMIDORESCONSUMIDORES
∫=
0
0
)(
q
dqqD
P
S/.porunidad
0 1 2 3 4 5 6 …….
Dem
anda
q
∫=
6
0
)( dqqD
Generalizando:
En el ejemplo….DTG
La disponibilidad total a gastar de los consumidores
refleja la utilidad total que alcanzan los consumidores.
La disponibilidad total a gastar de los consumidores
está representada por toda el área de la región que está por
debajo de la curva de demanda

24. ANÁLISIS 3:
EL GASTO DE LOS CONSUMIDORES
OfertaE
q
Dem
anda
0 1 2 3 4 5 6 …….
PS/.porunidad
4
3
2
Si se define al gasto
como p.q....
¿Cuál sería el gasto efectuado por los
consumidores en este ejemplo?
RTA: S/. 8
¿Cuál sería el área respectiva?
Gasto
RTA….

25. ANÁLISIS FINAL:
EL EXCEDENTE DE LOS CONSUMIDORES
∫=
4
0
)( dqqD
q
Dem
anda
0 1 2 3 4 5 6 …….
PS/.porunidad
4
3
2
q
Dem
anda
0 1 2 3 4 5 6 …….
PS/.porunidad
4
3
2
Análisis 2 La disponibilidad a gastar en este
caso es….
Gasto
Análisis 3
El gasto efectivo (lo que realmente
gastan) en este caso es…. = 8u2
Finalmente…. - Todos aquellos consumidores que estuvieron
dispuestos a pagar un precio mayor que el del
mercado (S/.2 por unidad), se benefician
El área que representa dicho “excedente” es el
EXCEDENTE DEL CONSUMIDOR :
Área de Disponibilidad total – Área de Gasto

26. ∫ −=
4
0
)4)(2()( dqqDEC
∫ −=
0
0
00)(
q
qpdqqDEC
Resultado del ejemplo
En este ejemplo…
Generalizando:
p = D(q)
2
0 4 q
p
EC

27. EJERCICIO MATEMÁTICOEJERCICIO MATEMÁTICO
 La ecuación de demanda para un producto es
p = D(q) = -q2
+25, para
0 < q < 5. Sabiendo que p es el precio por
unidad en dólares y q la cantidad de unidades
demandadas.
(a) ¿Cuál es la disponibilidad total de gasto de los
consumidores de este mercado, si se sabe que
el precio de mercado asciende a $9?
(b) ¿Cuál es el EC?
50 ≤≤ p

28. 28
)(qSp =
p
q
0p
0q
Excedente del
Productor
EXCEDENTE DEL PRODUCTOREXCEDENTE DEL PRODUCTOR
Ingreso real

29. 29
Excedente del productor
Si se venden q0 unidades a p0 dólares la unidad y si
p = S(q) es la función de oferta de los productores del
artículo, entonces:
∫−=
0
0
00 )(
q
dqqSqpEP

30. 30
EJEMPLO 3EJEMPLO 3
Dada la curva oferta p = S(q) = 0,3q2
+ 30
dólares
a) Determine el precio p0 = D(q0) al cual se ofertarán q0
= 4 unidades.
b) Trace la curva de oferta y sombree la región que
representa el excedente del productor para q0 = 4 .
c) Calcule el excedente del productor para q0 = 4 .