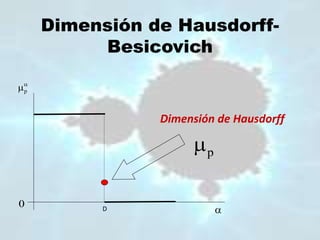
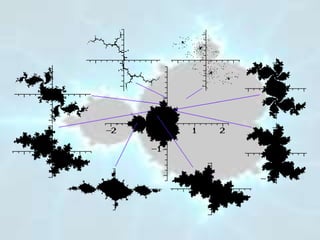
Este documento trata sobre los fractales y su aplicación en diferentes ámbitos. Brevemente resume algunas de sus propiedades fundamentales como la autosimilitud y dimensión fraccionaria. Luego presenta ejemplos de fractales matemáticos como la curva de Koch y el triángulo de Sierpinski, así como su presencia en la naturaleza en objetos como árboles, montañas y pulmones. Finalmente, describe aplicaciones de los fractales en medicina, cardiología, economía y finanzas para el análisis de señales cere

1. La complejidad del sistema
económico: herramientas
matemáticas para su análisis.
Dr. Juan E. Nápoles V.
Facultad de Ciencias Económicas
UNNE
2015

2. LOS FRACTALES
EL INFINITO AL ALCANCE DE LA MANO

5. En pasos de 100 Km el resultado es 2.400 Kms
En pasos de 50 Km el resultado es 3.050 Kms
En pasos de 25 Km el resultado es 3.625 Kms
En pasos de 10 metros el resultado es 45.500 Kms
En pasos de 5 metros el resultado es 54.000 Kms
(como dato de comparación: el ecuador terrestre mide 40.000
Kms)

9. Término acuñado por Mandelbrot en
1975 por la fusión (?) de las palabras
fractus (romper) y fracture (fractura),
dando una función doble
(sustantivo/adjetivo) a su creación.

10. Un fractal es un conjunto de puntos,
cuya dimensión no necesariamente es
entera, es decir, puede tener dimensión
fraccionaria y puede ser caracterizado
por las siguientes propiedades:
 Infinitud o nulidad.
 Autosimilitud.
 Compleja estructura a cualquier
escala.

11. La autosimilitud es un concepto que se
puede entender de una forma muy
intuitiva; a grandes rasgos, visualicemos
un objeto geométrico, o una figura,
ahora imaginemos que esta figura
está compuesta de figuras más pequeñas,
cada una de las cuales se ve idéntica a la
figura original excepto por el tamaño; y a
su vez cada una de estas figuras más
pequeñas se compone de figuritas todavía
más pequeñas y así sucesivamente...

12.   ,)(inf)(
1)(




k
p
k
Xd
p XdextX
i 


Sea p un número real no negativo arbitrario, 0p<
y dado >0, definamos
Cuando 0, el número

p
Tiende de manera monótona creciente a un
determinado límite (finito o infinito) que depende
de p, y que sirve para definir la dimensión de
conjunto, debido a que el límite toma um valor
finito y no nulo, a lo sumo, para um valor de p.

13. D
p
0
Dimensión de Hausdorff

p
Dimensión de Hausdorff-
Besicovich

14. K. Weierstrass (1815-1897) G. Cantor (1815-1897)

15. A. M. Lyapunov (1857-1918) G. Peano (1858-1932)

16. N. Von Koch (1815-1897) W. Sierpinski (1882-1969)

17. G. Julia (1893-1978) B. Mandelbrot (1924-2010)

18.  Los fractales matemáticos,
 Los fractales naturales (árboles,
montañas, nubes, etc.), y
 Los fractales humanos.

20. CLASIFICACIÓN
• Fractales como límites de
poligonales.
• Fractales como límites de
areas.
• Fractales como límites de
volúmenes.

22. La Curva de Von Koch se construye recursivamente
k=1
k=2
k=3
k=4
……………… …..
k infinito

23. La Curva de Von Koch es autosemejante, es más . . .
. . . Si la ampliamos con un zoom x3…
. . . obtenemos 4 copias de la curva original…

25. Triángulo de Sierpinski
Este triángulo es uno de los
pocos fractales que se puede
dibujar sin ayuda de una
computadora bajo las siguientes
instrucciones:

27.  La escalera del diablo.
 El helecho
 Orbitas caóticas.

29. La escalera del diablo
Agregar alturas al Conjunto de Cantor.

30. …Hay objetos que son “más que una curva”
pero sin llegar a ser una superficie…
Por ejemplo, la Curva de Peano
Podría pensarse que es unidimensional por ser una
curva, pero es bidimensional porque el límite cubre
todo el cuadrado.

31. Otra quimera matemática es la extensión del
Triángulo de Sierpinski:

32. El helecho
Michael Barnsley
tomó un camino
diferente; en vez de
generar los fractales
iterativamente, él
convirtió el azar en
el bloque
fundamental de los
fractales, y a esta
nueva técnica la
denominó "EL
JUEGO DE
CAOS"

33. El Conjunto de Mandelbrot
Zn+1 = (Zn)2 + Zo
Se construye en el plano complejo, recursivamente,
partiendo de un valor inicial Zo y calculando los siguientes
valores como
(Z0)  Z1  Z2  ...  Zn  Zn+1  ...
¿Para qué valores Zo esta sucesión se va a infinito?
¿Con qué rapidez se va a infinito?

34. Si pintamos los puntos que se van a a infinito de blanco
obtenemos el siguiente gráfico

35. El Conjunto Mandelbrot M, consiste de
todos aquellos valores (complejos) de c
cuyas órbitas de 0 bajo z2 + c
correspondientes, no escapan al infinito
{c / órbita de 0 en Z2+c converge}

36. El Mundo Mandelbrot
El conjunto de
Mandelbrot es,
como dijo James
Gleick, “el objeto
más complejo de
las Matemáticas”

37. CONJUNTOS DE JULIA
En el plano complejo, la sucesión
Zn+1=Zn
2+C,
determina, para cada valor de C, un
Conjunto de Julia, que está formado por
los Z0 cuyas órbitas convergen.

39. El fractal de Mandelbrot
Es una de esas
curvas que desafía
nuestra capacidad
de entendimiento
"geométrico", muy
habituada a las
estructuras
euclídeas, simples y
prácticas.

40. Característica fractal de
Mandelbrot
Una de las características
más espectaculares de
estos fractales, es que son
no derivables en todos sus
puntos. En lenguaje menos
matemático: una curva
cualquiera es no derivable
en un punto cuando, aun
existiendo ese punto, forma
un pico o esquina.

41. La figura muestra
una zona del fractal
de Mandelbrot
bastante parecida a
la figura de la
diapositiva anterior.

42. Pero al ampliar la
zona del punto A,
observamos que las
cosas se complican:
aparecen más y más
picos por todos
sitios...

44. Modelando la Naturaleza
¿La geometría clásica sirve para representar la
Naturaleza?
¿podemos representar una nube
con rectas, circunferencias y
curvas?

45. Árboles, foto del autor

46. Helechos, foto del autor

47. Imagen de la página de Paul Bourke http://local.wasp.uwa.edu.au/~pbourke/fractals/selfsimilar/

48. Patrones de autosemejanza en una hoja, foto del autor

49. Formas fractales vegetales, foto del autor

50. Formas fractales vegetales, foto del autor

51. Formas fractales vegetales, foto del autor

52. Formas fractales animales, foto del autor

53. Formas fractales inanimadas, foto del autor

54. Formas fractales inanimadas, foto del autor

55. La Curva de Von Koch aparece en la Naturaleza…

56. ¿Cómo son los anillos de Saturno?
Desde su descubrimiento por Galileo se pensó
que era un único anillo…

57. Con la evolución de los telescopios se probó que había
muchos…
…y que se distribuían como el Conjunto de Cantor…

65. Algunas de estas ideas, se usan en la tecnología,
por ejemplo, en el diseño de circuitos y antenas.

67. 3<5<7<9<11<...<3.2<5.2<...<3.22<5.22<...<23<22<2<1
Teorema. Si una función continua f:RR tiene un
punto periódico con período k, entonces también
tiene un punto con período n, para cada k<n (en (1)).

68. xn+1 =.xn (1-xn ),
A medida que  crece de 3 a 4 existen grandes
variaciones en la estructura del sistema.

70. Resumiendo los resultados experimentales para 3
en una tabla se tiene
n  incremento
en 
Cociente
entre
incrementos
sucesivos
1
2
3
4
5
6
7
8
3,000000
3,449499
3,544090
3,564407
3,568759
3,569692
3,569891
3,569934
-
0,449499
0,094591
0,020313
0,004352
0,000933
0,000199
0,000043
-
-
4,752027148
4,656673067
4,667509191
4,664523044
4,688442211
4,627906977

71. A partir de una transformación geométrica
sencilla realizada en un anillo, Steve Smale, en
Berkeley, elaboró un atractor extraño, el
“solenoide”, que traza una especie de ovillo de
hilos enrollados alrededor de un eje.

72. Representación esquemática de un atractor general,
denotado aquí por una A negra: las regiones próximas
(sombreadas) se contraen hacia el atractor a medida que
pasa el tiempo.

74. Aplicaciones Fractales y…
Algo más¡¡¡¡¡

75. Fractales en Medicina - Neurociencias
Simulación de una imágen del Cerebro
Humano
Iteración de la fórmula: Zn+1 = Z0 + C
Diferencia con el Conjunto de Mandelbrot, se colorean
TODOS los puntos y no solo los convergentes.
Modelo de Neurona con el que trabaja la
Medicina Actual
Primeros pasos para desarrollar un modelo
Neuronal Fractal.
Se elige un generador (A), se propone un
algoritmo (B) se comienza a desarrollar el
fractal (C y D).
Se puede llegar a diferentes modelos
dependiendo el generador y algoritmo
elegido.

76. Mas Fractales en Medicina
Imagen de un Pulmón humano
con características fractales
Imagen de un Pulmón animalcon
las mismas características
Fractales, Estadística y
Medicina
El análisis de autosimilitud y
patrones, no necesariamente tiene
que estudiarse desde imagenes,
puede hacerse tambien desde
ecuaciones o curvas como en este
caso de EEG o Series de Tiempo
Imagen de aumentada con detalles
de un pulmón humano

77. Cardiología Fractal
ECG visto como una serie de tiempo.
Se realiza un análisis Fractal para determinar la DF de ECG de pacientes sanos y de
pacientes con determinadas patologías.
Problema:
Diversos estudios de ECG mostraban una inconsistencia entre el tamaño de la arteria
izquierda en relación con la fibrilación arterial.
Hipótesis:
Mediante un Análisis de la Dimensión Fractal de una fibrilación arterial proveniente de
un ECG se puede predecir el tamaño de la arteria izquierda.
Método:
Se estudian 53 pacientes con fibrilación arterial.
Resultados:
Si la DF es mayor a 1.14, el tamaño de la arteria izquierda en TODOS los pacientes, es
de 4,6 cm. o mayor.
Si la DF es menor que 1.09 , el tamaño de la arteria izquierda en TODOS los pacientes,
es menor a 4,6 cm.
Si la DF se encuentra entre 1.09 y 1.14, no presenta una correlación con el tamaño de
la arteria izquierda.

78. Series de Tiempo como Fractales Caóticos
Con el mismo procedimiento descrito
anteriormente se genera un fractal lineal,
con autosimilitud perfecta, que
representa el gráfico de una serie de
tiempo.
La evolución y dinámica de diferentes sistemas biológicos, sociales,
económicos o médicos pueden ser vistos y representados como series
de tiempo.
Gráfico de la evolución
de precios en la Bolsa
de Comercio de Canadá,
la cual puede ser tratada
y estudiada como una
serie de tiempo.
Un
ElectroEncefalograma
también puede ser visto
y tratado como una
serie de tiempo
En ambos casos se realiza un Análisis Fractal para determinar el grado de
autosimilitud que poseen estas series, y en base a eso se puede conocer más
acerca de su dinámica, lo cual permite realizar inferencias sobre el sistema.

79. Fractales en Economía y Finanzas
Teoría Multifractal en el
Análisis de la Bolsa de
Comercio
A la izquierda modelos tradiconales en el
Análisis de charts. A la derecha el mismo
Análisis pero utilizando técnicas Fractales
Notar la diferencia en el detalle.

80. Enconomía Fractal
Mercados Financieros vistos como series de tiempo.
Se realiza un Análisis para determinar la DF de la serie de tiempo con el objeto de conocer la dinámica del movimiento de precios
dentro de la Bolsa de Comercio y poder inferir sobre valores futuros.
Se calcula la DF mediante el algoritmo denominado Exponente de Hurst.
Propiedades del exponente de Hurst (H):
Varía entre 0 y 1
Si H = 0,5 del exponente indica que la serie de tiempo es TOTALMENTE aleatoria por lo cual no se puede inferir en el futuro.
Si 0 < H < 0,5 existe una correlación inversa. Si la tendencia de la serie era decreciente, en intervalos posteriores será creciente, y
por el contrario, si su tendencia era creciente, en el futuro será decreciente.
Si 0,5 < H < 1 existe una correlación directa. Si en un intervalo de tiempo la serie es creciente, lo seguirá siendo en el futuro, y
viceversa.
Aplicación al Mercado Financiero.
Si se estudia la evolución en el tiempo del precio de determinada acción mediante esta técnica se puede inferir:
Si el valor de H de la serie de tiempo es 0,5 no puedo decidir que hacer con mis acciones.
Si 0 < H < 0,5 && previamente creciente => VENDO (infiero que luego el valor disminuyendo)
Si 0 < H < 0,5 && previamente decreciente => COMPRO (infiero que luego el valor aumentará)
Si 0,5 < H < 1 && previamente creciente => COMPRO (infiero que el valor seguirá aumentando)
Si 0,5 < H < 1 && previemante decreciente = > VENDO (infiero que el valor seguirá disminuyendo)

81. Análisis Fractal de índices bursátiles
Análisis del índice de valores de las acciones de la empresa
Google, perteneciente al indicador de acciones tecnológicas
de EEUU NASDAQ.
Período: Desde el primer día de cotización hasta Setiembre
de 2008 donde se produce el crash financiero.
El índice tiene un piso de 100 U$S y llegó a cotizar
780 U$S.
El índice fractal calculado de esta serie de tiempo (el
Exponente de Hurst), tiene un valor de 0,58.
Lo cual indica que el movimiento de precios tuvo una
dinámica cercana a la aleatoriedad.
Análisis del índice de valores de las acciones de la Bolsa de
Comercio de Buenos Aires, MERVAL, del día 22 de Octubre
de 2008.
Este día las acciones han tenido una caída del 10%.
El índice fractal calculado ha sido de 0.75%.
El mismo es significativamente superior a 0,5,. Lo cual
indica una dinámica alejada de la aleatoriedad, esto significa
que hubo coordinación en la compra y venta de acciones a
lo largo de ese mismo día. Miles de mentes pensaron lo
mismo al mismo tiempo.
Mediante este tipo de análisis es posible sacar patrones de
comportamiento y comprender con mayor eficacia la
dinámica de un sistema hiper-complejo como la Bolsa de

82. Fractales y Arquitectura
Arte Fractal
Estas tres imagenes de Arte
Fractal muestran Fractales
matemáticos perfectamente
reconocibles, el Conjunto de
Mandelbro y el Conjunto de
Julia
Fractales manipulados
mediante un software
para generar paisajes
Fractales, utilizados en el
cine o videos para suplantar
maquetas.

83. ¿Qué son los
fractales?

96. .

101. Aprecia el arte de la
Naturaleza a tu
alrededor.